2.1.4: Dilations on a Square Grid

Lesson

Let's dilate figures on a square grid.

Exercise \(\PageIndex{1}\): Estimating a Scale Factor

Figure \(\PageIndex{1}\)

Point \(C\) is the dilation of point \(B\) with center of dilation and scale factor . Estimate . Be prepared to explain your reasoning.

Exercise \(\PageIndex{2}\): Dilations on a Grid

1. Find the dilation of quadrilateral \(ABCD\) with center \(P\) and scale factor 2.

Figure \(\PageIndex{2}\)

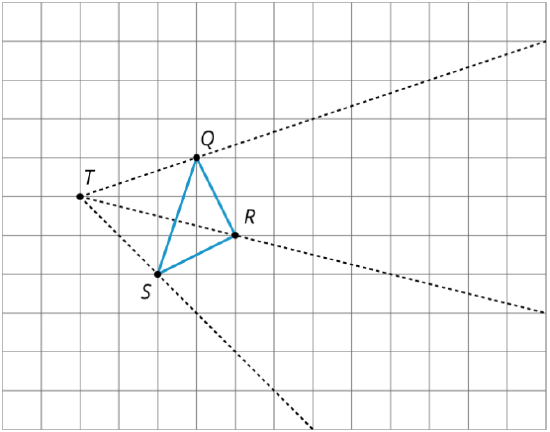
2. Find the dilation of triangle \(QRS\) with center \(T\) and scale factor \(2\).

3. Find the dilation of triangle \(QRS\) with center \(T\) and scale factor \(\frac{1}{2}\).

Figure \(\PageIndex{3}\): Point T, triangle Q R S and three projection rays on a square grid. Let the lower left corner be (0 comma 0). Then triangle Q R S is Q(5 comma 7), R(6 comma 5), S(4 comma 4) and point T is T(2 comma 6). The dashed projection rays are T Q, T R and T S.

Exercise \(\PageIndex{3}\): Card Sort: Matching Dilations on a Coordinate Grid

Your teacher will give you some cards. Each of Cards 1 through 6 shows a figure in the coordinate plane and describes a dilation.

Each of Cards A through E describes the image of the dilation for one of the numbered cards.

Match number cards with letter cards. One of the number cards will not have a match. For this card, you’ll need to draw an image.

Are you ready for more?

The image of a circle under dilation is a circle when the center of the dilation is the center of the circle. What happens if the center of dilation is a point on the circle? Using center of dilation \((0,0)\) and scale factor 1.5, dilate the circle shown on the diagram. This diagram shows some points to try dilating.

Figure \(\PageIndex{4}\): Five points on a circle on a coordinate plane, origin O. Horizontal axis scale negative 1 to 13 by 1’s. Vertical axis scale negative 6 to 6 by 1’s. Circle has radius 4 and is centered at (4 comma 0). The five points on the circle are B(0 comma 0), C(point 5 comma 2), H(3 comma 4), D(7 point 5 comma 2) and G(3 comma negative 4).

Summary

Square grids can be useful for showing dilations. The grid is helpful especially when the center of dilation and the point(s) being dilated lie at grid points. Rather than using a ruler to measure the distance between the points, we can count grid units.

For example, suppose we want to dilate point \(Q\) with center of dilation \(P\) and scale factor \(\frac{3}{2}\). Since \(Q\) is 4 grid squares to the left and 2 grid squares down from \(P\), the dilation will be 6 grid squares to the left and 3 grid squares down from \(P'\) (can you see why?). The dilated image is marked as \(Q'\) in the picture.

Figure \(\PageIndex{5}\)

Sometimes the square grid comes with coordinates. The coordinate grid gives us a convenient way to name points, and sometimes the coordinates of the image can be found with just arithmetic.

For example, to make a dilation with center \((0,0)\) and scale factor 2 of the triangle with coordinates \((-1,-2)\), \((3,1)\), and \((2,-1)\), we can just double the coordinates to get \((-2,-4)\), \((6,2)\), and \((4,-2)\).

Figure \(\PageIndex{6}\): Two triangles on a coordinate plane, origin O. Horizontal axis scale negative 7 to 7 by 1’s. Vertical axis scale negative 5 to 5 by 1’s. The coordinates of the triangle are (negative 1 comma negative 2), (3 comma 1), (2 comma negative 1 ). The coordinates of the image are(negative 2 comma negative 4), (6 comma 2), (4 comma negative 2).

Glossary

Definition: Center of a Dilation

The center of a dilation is a fixed point on a plane. It is the starting point from which we measure distances in a dilation.

In this diagram, point \(P\) is the center of the dilation.

Figure \(\PageIndex{4}\)

Definition: Dilation

A dilation is a transformation in which each point on a figure moves along a line and changes its distance from a fixed point. The fixed point is the center of the dilation. All of the original distances are multiplied by the same scale factor.

For example, triangle \(DEF\) is a dilation of triangle \(ABC\). The center of dilation is \(O\) and the scale factor is 3.

This means that every point of triangle \(DEF\) is 3 times as far from \(O\) as every corresponding point of triangle \(ABC\).

Figure \(\PageIndex{5}\)

Definition: Scale Factor

To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.

In this example, the scale factor is 1.5, because \(4\cdot (1.5)=6\), \(5\cdot (1.5)=7.5\), and \(6\cdot (1.5)=9\).

Figure \(\PageIndex{6}\)

Practice

Exercise \(\PageIndex{4}\)

Triangle \(ABC\) is dilated using \(D\) as the center of dilation with scale factor \(2\).

The image is triangle \(A'B'C'\). Clare says the two triangles are congruent, because their angle measures are the same. Do you agree? Explain how you know.

Figure \(\PageIndex{7}\): Triangle A B C, it’s image after dilation triangle A prime B prime C prime and point D. Point D is on the right, smaller triangle A B C is in the middle and larger image triangle A prime, B prime and C prime is on the right.

Exercise \(\PageIndex{5}\)

On graph paper, sketch the image of quadrilateral PQRS under the following dilations:

1. The dilation centered at \(R\) with scale factor \(2\).
2. The dilation centered at \(O\) with scale factor \(\frac{1}{2}\).
3. The dilation centered at \(S\) with scale factor \(\frac{1}{2}\).

Figure \(\PageIndex{8}\): Quadrilateral P Q R S and point O on a square grid. Let the lower left corner be (0 comma 0). Then the coordinates of P Q R S are P(7 comma 6), Q(5 comma 4), R(9 comma 3), S(11 comma 5). The coordinates of point O are O(5 comma 1).

Exercise \(\PageIndex{6}\)

The diagram shows three lines with some marked angle measures.

Figure \(\PageIndex{9}\):

A line slanting up and to the right. Two lines intersect this line, both slanting up and to the right, but do not intersect. At the first intersection, the top right angle is labeled 35 degrees. The rest are labeled ?. At the second intersection, the top right angle is labeled 27 degrees. The rest are labeled ?.

Find the missing angle measures marked with question marks.

(From Unit 1.4.4)

Exercise \(\PageIndex{7}\)

Describe a sequence of translations, rotations, and reflections that takes Polygon P to Polygon Q.

Figure \(\PageIndex{10}\)

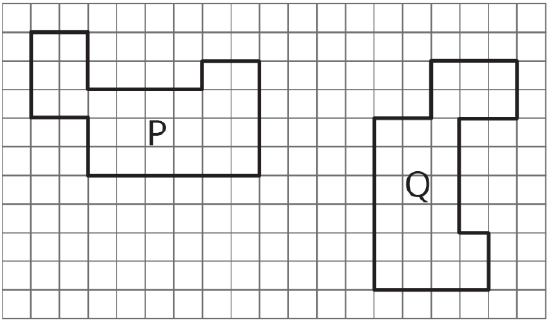
(From Unit 1.1.4)

Exercise \(\PageIndex{8}\)

Point \(B\) has coordinates \((-2,-5)\). After a translation 4 units down, a reflection across the -axis, and a translation 6 units up, what are the coordinates of the image?

(From Unit 1.1.6)