2.3.2: Writing Equations for Lines

Lesson

Let's explore the relationship between points on a line and the slope of the line.

Exercise \(\PageIndex{1}\): Coordinates and Lengths in the Coordinate Plane

Figure \(\PageIndex{1}\)

Find each of the following and explain your reasoning:

1. The length of segment \(BE\).
2. The coordinates of \(E\).

Exercise \(\PageIndex{2}\): What We Mean by an Equation of a Line

Line \(j\) is shown in the coordinate plane.

1. What are the coordinates of \(B\) and \(D\)?
2. Is point \((20, 15)\) on line \(j\)? Explain how you know.
3. Is point \((100, 75)\) on line \(j\)? Explain how you know.
4. Is point \((90, 68)\) on line \(j\)? Explain how you know.
5. Suppose you know the \(x\)- and \(y\)-coordinates of a point. Write a rule that would allow you to test whether the point is on line \(j\).

Figure \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\): Writing Relationships from Slope Triangles

Here are two diagrams:

1. Complete each diagram so that all vertical and horizontal segments have expressions for their lengths.
2. Use what you know about similar triangles to find an equation for the quotient of the vertical and horizontal side lengths of \(\Delta DFE\) in each diagram.

Figure \(\PageIndex{3}\)

Figure \(\PageIndex{4}\)

Are you ready for more?

1. Find the area of the shaded region by summing the areas of the shaded triangles.
2. Find the area of the shaded region by subtracting the area of the unshaded region from the large triangle.
3. What is going on here?

Figure \(\PageIndex{5}\)

Summary

Here are the points \(A\), \(C\), and \(E\) on the same line. Triangles \(ABC\) and \(ADE\) are slope triangles for the line so we know they are similar triangles. Let’s use their similarity to better understand the relationship between \(x\) and \(y\), which make up the coordinates of point \(E\).

Figure \(\PageIndex{6}\): Coordinate plane, x, negative 1 to 6, y negative 1 to 8. A line through 0 comma 0, point C at 1 comma 2, and point E at x comma y. A dotted line connects C to B at 1 comma 0. Another connects E to D at x comma 0. The length of E D is y. The distance from the the origin to D is x.

The slope for triangle \(ABC\) is \(\frac{2}{1}\) since the vertical side has length 2 and the horizontal side has length 1. The slope we find for triangle \(ADE\) is \(\frac{y}{x}\) because the vertical side has length \(y\) and the horizontal side has length \(x\). These two slopes must be equal since they are from slope triangles for the same line, and so: \(\frac{2}{1}=\frac{y}{x}\).

Since \(\frac{2}{1}=2\) this means that the value of \(y\) is twice the value of \(x\), or that \(y=2x\). This equation is true for any point \((x,y)\) on the line!

Here are two different slope triangles. We can use the same reasoning to describe the relationship between \(x\) and \(y\) for this point \(E\).

Figure \(\PageIndex{7}\): Coordinate plane, x, negative 1 to 6, y negative 1 to 8. A line through point A, at 0 comma 1, point C at 1 comma 3, and point E at x comma y. A dotted line connects C to B at 1 comma 1. Another connects E to D at x comma 1. The length of E D is y minus 1. The length of A, D is x.

The slope for triangle \(ABC\) is \(\frac{2}{1}\) since the vertical side has length 2 and the horizontal side has length 1. For triangle \(ADE\), the horizontal side has length \(x\). The vertical side has length \(y-1\) because the distance from \((x,y)\) to the \(x\)-axis is \(y\) but the vertical side of the triangle stops 1 unit short of the \(x\)-axis. So the slope we find for triangle \(ADE\) is \(\frac{y-1}{x}\). The slopes for the two slope triangles are equal, meaning: \(\frac{2}{1}=\frac{y-1}{x}\)

Since \(y-1\) is twice \(x\), another way to write this equation is \(y-1=2x\). This equation is true for any point \((x,y)\) on the line!

Glossary Entries

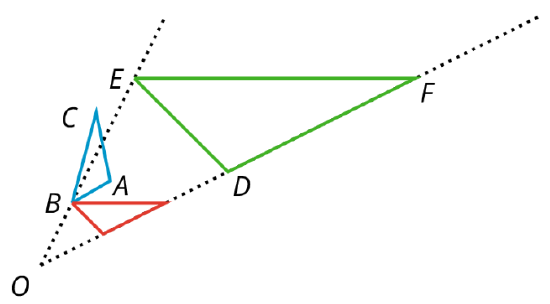
Definition: Similar

Two figures are similar if one can fit exactly over the other after rigid transformations and dilations.

In this figure, triangle \(ABC\) is similar to triangle \(DEF\).

If \(ABC\) is rotated around point \(B\) and then dilated with center point \(O\), then it will fit exactly over \(DEF\). This means that they are similar.

Figure \(\PageIndex{8}\)

Definition: Slope

The slope of a line is a number we can calculate using any two points on the line. To find the slope, divide the vertical distance between the points by the horizontal distance.

The slope of this line is 2 divided by 3 or \(\frac{2}{3}\).

Figure \(\PageIndex{9}\)

Practice

Exercise \(\PageIndex{4}\)

For each pair of points, find the slope of the line that passes through both points. If you get stuck, try plotting the points on graph paper and drawing the line through them with a ruler.

1. \((1,1)\) and \((7,5)\)
2. \((1,1)\) and \((5,7)\)
3. \((2,5)\) and \((-1,2)\)
4. \((2,5)\) and \((-7,-4)\)

Exercise \(\PageIndex{5}\)

Line \(l\) is shown in the coordinate plane.

1. What are the coordinates of points \(B\) and \(D\)?
2. Is the point \((16,20)\) on line \(l\)? Explain how you know.
3. Is the point \((20,24)\) on line \(l\)? Explain how you know.
4. Is the point \((80,100)\) on line \(l\)? Explain how you know.
5. Write a rule that would allow you to test whether \((x,y)\) is on line \(l\).

Figure \(\PageIndex{10}\)

Exercise \(\PageIndex{6}\)

Consider the graphed line.

Figure \(\PageIndex{11}\)

Mai uses Triangle A and says the slope of this line is \(\frac{6}{4}\). Elena uses Triangle B and says no, the slope of this line is 1.5. Do you agree with either of them? Explain.

Exercise \(\PageIndex{7}\)

A rectangle has length 6 and height 4.

Which of these would tell you that quadrilateral \(ABCD\) is definitely not similar to this rectangle? Select all that apply.

1. \(AB=BC\)
2. \(m\angle ABC=105^{\circ}\)
3. \(AB=8\)
4. \(BC=8\)
5. \(BC=2\cdot AB\)
6. \(2\cdot AB=3\cdot BC\)

(From Unit 2.2.1)