8.2.1: Finding Side Lengths of Triangles

Lesson

Let's find triangle side lengths.

Exercise \(\PageIndex{1}\): Which One Doesn't Belong: Triangles

Which triangle doesn't belong?

Figure \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\): A Table of Triangles

1. Complete the tables for these three triangles:

Figure \(\PageIndex{2}\)

Table \(\PageIndex{1}\)

triangle	\(a\)	\(b\)	\(c\)
\(D\)
\(E\)
\(F\)

Table \(\PageIndex{2}\)

triangle	\(a^{2}\)	\(b^{2}\)	\(c^{2}\)
\(D\)
\(E\)
\(F\)

2. What do you notice about the values in the table for Triangle E but not for Triangles D and F?

3. Complete the tables for these three more triangles:

Figure \(\PageIndex{3}\)

Table \(\PageIndex{3}\)

triangle	\(a\)	\(b\)	\(c\)
\(P\)
\(Q\)
\(R\)

Table \(\PageIndex{4}\)

triangle	\(a^{2}\)	\(b^{2}\)	\(c^{2}\)
\(P\)
\(Q\)
\(R\)

4. What do you notice about the values in the table for Triangle Q but not for Triangles P and R?

5. What do Triangle E and Triangle Q have in common?

Exercise \(\PageIndex{3}\): Meet the Pythagorean Theorem

1. Find the missing side lengths. Be prepared to explain your reasoning.
2. For which triangles does \(a^{2}+b^{2}=c^{2}\)?

Figure \(\PageIndex{4}\)

Figure \(\PageIndex{5}\)

Figure \(\PageIndex{6}\)

Are you ready for more?

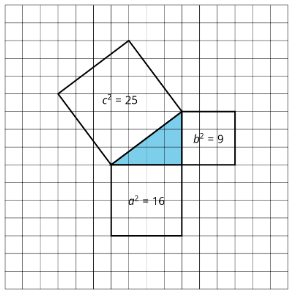
If the four shaded triangles in the figure are congruent right triangles, does the inner quadrilateral have to be a square? Explain how you know.

Figure \(\PageIndex{7}\): A square with side lengths of 14 units on a square grid. there is a second square inside the square. Each of the vertices of the inside square divides the side lengths of the large square into two lengths: 8 units and 6 units creating 4 right triangles.

Summary

A right triangle is a triangle with a right angle. In a right triangle, the side opposite the right angle is called the hypotenuse, and the two other sides are called its legs. Here are some right triangles with the hypotenuse and legs labeled:

Figure \(\PageIndex{8}\)

We often use the letters \(a\) and \(b\) to represent the lengths of the shorter sides of a triangle and \(c\) to represent the length of the longest side of a right triangle. If the triangle is a right triangle, then \(a\) and \(b\) are used to represent the lengths of the legs, and \(c\) is used to represent the length of the hypotenuse (since the hypotenuse is always the longest side of a right triangle). For example, in this right triangle, \(a=\sqrt{20}\), \(b=\sqrt{5}\), and \(c=5\).

Figure \(\PageIndex{9}\)

Here are some right triangles:

Figure \(\PageIndex{10}\)

Notice that for these examples of right triangles, the square of the hypotenuse is equal to the sum of the squares of the legs. In the first right triangle in the diagram, \(9+16=25\), in the second, \(1+16=17\), and in the third, \(9+9=18\). Expressed another way, we have \(a^{2}+b^{2}=c^{2}\). This is a property of all right triangles, not just these examples, and is often known as the Pythagorean Theorem. The name comes from a mathematician named Pythagoras who lived in ancient Greece around 2,500 BCE, but this property of right triangles was also discovered independently by mathematicians in other ancient cultures including Babylon, India, and China. In China, a name for the same relationship is the Shang Gao Theorem. In future lessons, you will learn some ways to explain why the Pythagorean Theorem is true for any right triangle.

It is important to note that this relationship does not hold for all triangles. Here are some triangles that are not right triangles, and notice that the lengths of their sides do not have the special relationship \(a^{2}+b^{2}=c^{2}\). That is, \(16+10\) does not equal 18, and \(2+10\) does not equal 16.

Figure \(\PageIndex{11}\)

Glossary Entries

Definition: Pythagorean Theorem

The Pythagorean Theorem describes the relationship between the side lengths of right triangles.

The diagram shows a right triangle with squares built on each side. If we add the areas of the two small squares, we get the area of the larger square.

The square of the hypotenuse is equal to the sum of the squares of the legs. This is written as \(a^{2}+b^{2}=c^{2}\).

Figure \(\PageIndex{12}\)

Definition: Hypotenuse

The hypotenuse is the side of a right triangle that is opposite the right angle. It is the longest side of a right triangle.

Here are some right triangles. Each hypotenuse is labeled.

Figure \(\PageIndex{13}\)

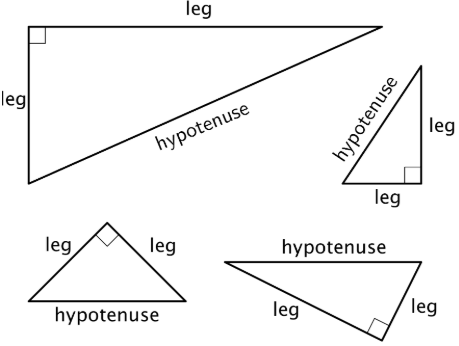
Definition: LEgs

The legs of a right triangle are the sides that make the right angle.

Here are some right triangles. Each leg is labeled.

Figure \(\PageIndex{14}\)

Practice

Exercise \(\PageIndex{4}\)

Here is a diagram of an acute triangle and three squares.

Figure \(\PageIndex{15}\): An acute triangle with squares along each side of the triangle. Each square has sides equal to the length of the side of the triangle it touches. The square on the bottom is touching the shortest side and is labeled 9. The square on the top right is touching the next longest side and is labeled 17. The square on the top left is touching the longest side and is unlabeled.

Priya says the area of the large unmarked square is 26 square units because \(9+17=26\). Do you agree? Explain your reasoning.

Exercise \(\PageIndex{5}\)

\(m\), \(p\), and \(z\) represent the lengths of the three sides of this right triangle.

Figure \(\PageIndex{16}\)

Select all the equations that represent the relationship between \(m\), \(p\), and \(z\).

1. \(m^{2}+p^{2}=z^{2}\)
2. \(m^{2}=p^{2}+z^{2}\)
3. \(m^{2}=z^{2}+p^{2}\)
4. \(p^{2}+m^{2}=z^{2}\)
5. \(z^{2}+p^{2}=m^{2}\)
6. \(p^{2}+z^{2}=m^{2}\)

Exercise \(\PageIndex{6}\)

The lengths of the three sides are given for several right triangles. For each, write an equation that expresses the relationship between the lengths of the three sides.

1. \(10, 6, 8\)
2. \(\sqrt{5}, \sqrt{3},\sqrt{8}\)
3. \(5,\sqrt{5},\sqrt{30}\)
4. \(1,\sqrt{37},6\)
5. \(3,\sqrt{2},\sqrt{7}\)

Exercise \(\PageIndex{7}\)

Order the following expressions from least to greatest.

\(25\div 10\qquad 250,000\div 1,000\qquad 2.5\div 1,000\qquad 0.025\div 1\)

(From Unit 4.1.1)

Exercise \(\PageIndex{8}\)

What is the best explanation for why \(-\sqrt{10}\) is irrational?

1. \(-\sqrt{10}\) is irrational because it is not rational.
2. \(-\sqrt{10}\) is irrational because it is less than zero.
3. \(-\sqrt{10}\) is irrational because it is not a whole number.
4. \(-\sqrt{10}\) is irrational because if I put \(-\sqrt{10}\) into a calculation, I get \(-3.16227766\), which does not make a repeating pattern.

(From Unit 8.1.3)

Exercise \(\PageIndex{9}\)

A teacher tells her students she is just over \(1\) and \(\frac{1}{2}\) billion seconds old.

1. Write her age in seconds using scientific notation.
2. What is a more reasonable unit of measurement for this situation?
3. How old is she when you use a more reasonable unit of measurement?

(From Unit 7.3.7)