8.2.2: A Proof of the Pythagorean Theorem

Lesson

Let's prove the Pythagorean Theorem.

Exercise \(\PageIndex{1}\): Notice and Wonder: A Square and Four Triangles

Figure \(\PageIndex{1}\)

What do you notice? What do you wonder?

Exercise \(\PageIndex{2}\): Adding Up Areas

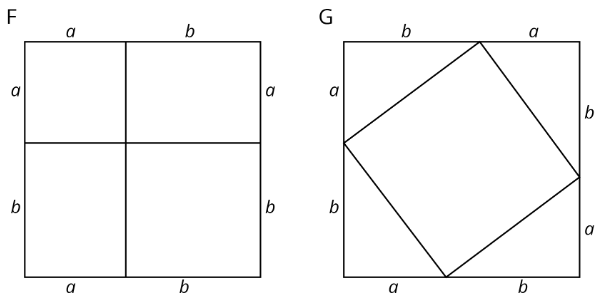
Both figures shown here are squares with a side length of \(a+b\). Notice that the first figure is divided into two squares and two rectangles. The second figure is divided into a square and four right triangles with legs of lengths \(a\) and \(b\). Let’s call the hypotenuse of these triangles \(c\).

Figure \(\PageIndex{2}\)

1. What is the total area of each figure?
2. Find the area of each of the 9 smaller regions shown the figures and label them.
3. Add up the area of the four regions in Figure F and set this expression equal to the sum of the areas of the five regions in Figure G. If you rewrite this equation using as few terms as possible, what do you have?

Are you ready for more?

Take a 3-4-5 right triangle, add on the squares of the side lengths, and form a hexagon by connecting vertices of the squares as in the image. What is the area of this hexagon?

Figure \(\PageIndex{3}\)

Exercise \(\PageIndex{3}\): Let's Take it for a Spin

Find the unknown side lengths in these right triangles.

Figure \(\PageIndex{4}\)

Exercise \(\PageIndex{4}\): A Transformational Proof

Use the applets to explore the relationship between areas.

• Consider Squares \(A\) and \(B\).
• Check the box to show the pieces.
• Check the box to turn \(C\).
• Arrange the five pieces to fit inside Square \(C\).
• Check the box to see the right triangle.
• Arrange the figures so the squares are adjacent to the sides of the triangle.

1. If the right triangle has legs \(a\) and \(b\) and hypotenuse \(c\), what have you just demonstrated to be true?
2. Try it again with different squares. Estimage the areas of the new Squares, \(A\), \(B\), and \(C\) and explain what you observe.
3. Estiamte the areas of these new Squares, \(A\), \(B\), and \(C\), and then explain what you observe as you complete the activity.
4. What do you think we may be able to conclude?

Summary

The figures shown here can be used to see why the Pythagorean Theorem is true. Both large squares have the same area, but they are broken up in different ways. (Can you see where the triangles in Square G are located in Square F? What does that mean about the smaller squares in F and H?) When the sum of the four areas in Square F are set equal to the sum of the 5 areas in Square G, the result is \(a^{2}+b^{2}=c^{2}\), where \(c\) is the hypotenuse of the triangles in Square G and also the side length of the square in the middle. Give it a try!

Figure \(\PageIndex{5}\)

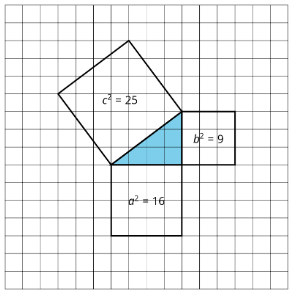
This is true for any right triangle. If the legs are \(a\) and \(b\) and the hypotenuse is \(c\), then \(a^{2}+b^{2}=c^{2}\). This property can be used any time we can make a right triangle. For example, to find the length of this line segment:

Figure \(\PageIndex{6}\)

The grid can be used to create a right triangle, where the line segment is the hypotenuse and the legs measure 24 units and 7 units:

Figure \(\PageIndex{7}\)

Since this is a right triangle, \(24^{2}+7^{2}=c^{2}\). The solution to this equation (and the length of the line segment) is \(c=25\).

Glossary Entries

Definition: Pythagorean Theorem

The Pythagorean Theorem describes the relationship between the side lengths of right triangles.

The diagram shows a right triangle with squares built on each side. If we add the areas of the two small squares, we get the area of the larger square.

The square of the hypotenuse is equal to the sum of the squares of the legs. This is written as \(a^{2}+b^{2}=c^{2}\).

Figure \(\PageIndex{8}\)

Definition: Hypotenuse

The hypotenuse is the side of a right triangle that is opposite the right angle. It is the longest side of a right triangle.

Here are some right triangles. Each hypotenuse is labeled.

Figure \(\PageIndex{9}\)

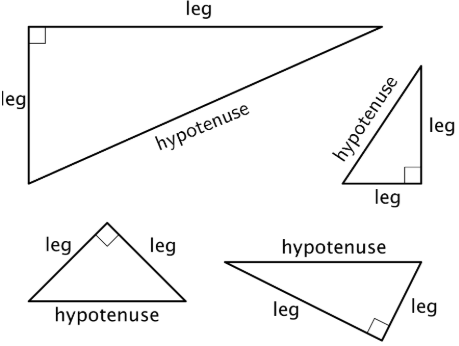
Definition: LEgs

The legs of a right triangle are the sides that make the right angle.

Here are some right triangles. Each leg is labeled.

Figure \(\PageIndex{10}\)

Practice

Exercise \(\PageIndex{5}\)

1. Find the lengths of the unlabeled sides.

Figure \(\PageIndex{11}\)

Figure \(\PageIndex{12}\)

2. One segment is \(n\) units long and the other is \(p\) units long. Find the value of \(n\) and \(p\). (Each small grid square is 1 square unit.)

Figure \(\PageIndex{13}\)

Figure \(\PageIndex{14}\)

Exercise \(\PageIndex{6}\)

Use the areas of the two identical squares to explain why \(5^{2}+12^{2}=13^{2}\) without doing any calculations.

Figure \(\PageIndex{15}\)

Exercise \(\PageIndex{7}\)

Each number is between which two consecutive integers?

1. \(\sqrt{10}\)
2. \(\sqrt{54}\)
3. \(\sqrt{18}\)
4. \(\sqrt{99}\)
5. \(\sqrt{41}\)

(From Unit 8.1.5)

Exercise \(\PageIndex{8}\)

1. Give an example of a rational number, and explain how you know it is rational.
2. Give three examples of irrational numbers.

(From Unit 8.1.3)

Exercise \(\PageIndex{9}\)

Write each expression as a single power of 10.

1. \(10^{5}\cdot 10^{0}\)
2. \(\frac{10^{9}}{10^{0}}\)

(From Unit 7.2.3)

Exercise \(\PageIndex{10}\)

Andre is ordering ribbon to make decorations for a school event. He needs a total of exactly 50.25 meters of blue and green ribbon. Andre needs 50% more blue ribbon than green ribbon for the basic design, plus an extra 6.5 meters of blue ribbon for accents. How much of each color of ribbon does Andre need to order?

(From Unit 4.3.6)