6.2.2: Reasoning about Solving Equations (Part 2)

Lesson

Let's use hangers to understand two different ways of solving equations with parentheses.

Exercise \(\PageIndex{1}\): Equivalent to \(2(x+3)\)

Select all the expressions equivalent to \(2(x+3)\).

1. \(2\cdot (x+3)\)
2. \((x+3)2\)
3. \(2\cdot x+2\cdot 3\)
4. \(2\cdot x+3\)
5. \((2\cdot x)+3\)
6. \((2+x)3\)

Exercise \(\PageIndex{2}\): Either Or

1. Explain why either of these equations could represent this hanger:

Figure \(\PageIndex{1}\)

\(14=2(x+3)\) or \(14=2x+6\)

2. Find the weight of one circle. Be prepared to explain your reasoning.

Exercise \(\PageIndex{3}\): Use Hangers to Understand Equation Solving, Again

Here are some balanced hangers. Each piece is labeled with its weight.

Figure \(\PageIndex{2}\): Four balanced hanger diagram. First diagram, left side, two groups, each group has circle x, square 5, right side, rectangle, 16. Second diagram, left side, two groups, each group has triangle y, square 200, right side, rectangle, 3000. Third diagram, left side, rectangle 20 point 8, right side 4 groups, each group has pentagon z, square 1 point 1. Fourth diagram, left side, rectangle, 20 over 3, left side, two groups, each group has crown w and square 2 over 3.

1. Assign one of these equations to each hanger:
   \[\begin{array}{lll}{2(x+5)=16}&{\qquad}&{3(y+200)=3,000}\\{20.8=4(z+1.1)}&{\qquad}&{\frac{20}{3}=2(w+\frac{2}{3})}\end{array}\nonumber\]
2. Explain how to figure out the weight of a piece labeled with a letter by reasoning about the diagram.
3. Explain how to figure out the weight of a piece labeled with a letter by reasoning about the equation.

Summary

The balanced hanger shows 3 equal, unknown weights and 3 2-unit weights on the left and an 18-unit weight on the right.

There are 3 unknown weights plus 6 units of weight on the left. We could represent this balanced hanger with an equation and solve the equation the same way we did before.

Figure \(\PageIndex{3}\)

\(\begin{aligned}3x+6&=18 \\ 3x&=12 \\ x&=4\end{aligned}\)

Since there are 3 groups of \(x+2\) on the left, we could represent this hanger with a different equation: \(3(x+2)=18\).

Figure \(\PageIndex{4}\)

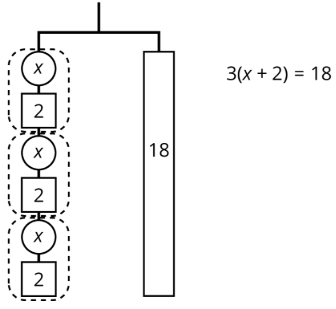
The two sides of the hanger balance with these weights: 3 groups of \(x+2\) on one side, and 18, or 3 groups of 6, on the other side.

Figure \(\PageIndex{5}\): Balanced hanger, left side, circle labeled x, square labeled 2, circle labeled x, square labeled 2, circle labeled x, square labeled 2, right side, rectangle not labeled. A dotted line is drawn around three groups, each group contains one circle and one square from the left side and a third of the rectangle on the right side. To the side, an equation says 3 ( x + 2 ) = 18.

The two sides of the hanger will balance with \(\frac{1}{3}\) of the weight on each side: \(\frac{1}{3}\cdot 3(x+2)=\frac{1}{3}\cdot 18\).

Figure \(\PageIndex{6}\)

We can remove 2 units of weight from each side, and the hanger will stay balanced. This is the same as subtracting 2 from each side of the equation.

Figure \(\PageIndex{7}\): Balanced hanger. Left side, circle labeled x and square labeled 2, the square appears to be loose from the hanger. Right side, rectangle labeled 4 and square labeled 2, the square appears to be loose from the hanger. To the side, and equation says x + 2 = 4 + 2.

An equation for the new balanced hanger is \(x=4\). This gives the solution to the original equation.

Figure \(\PageIndex{8}\)

Here is a concise way to write the steps above:

\(\begin{array}{lr}{3(x+2)=18}&{}\\{x+2=6}&{\text{after multiplying each side by }\frac{1}{3}}\\{x=4}&{\text{after subtracting }2\text{ from each side}}\end{array}\)

Practice

Exercise \(\PageIndex{4}\)

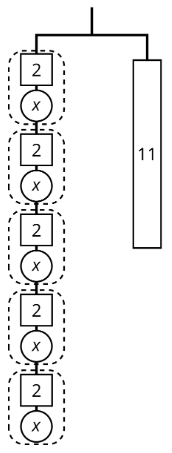
Here is a hanger:

1. Write an equation to represent the hanger.
2. Solve the equation by reasoning about the equation or the hanger. Explain your reasoning.

Figure \(\PageIndex{9}\)

Exercise \(\PageIndex{5}\)

Explain how each part of the equation \(9=3(x+2)\) is represented in the hanger.

Figure \(\PageIndex{10}\)

• \(x\)
• \(9\)
• \(3\)
• \(x+2\)
• \(3(x+2)\)
• the equal sign

Exercise \(\PageIndex{6}\)

Select the word from the following list that best describes each situation.

1. You deposit money in a savings account, and every year the amount of money in the account increases by 2.5%.
2. For every car sold, a car salesman is paid 6% of the car’s price.
3. Someone who eats at a restaurant pays an extra 20% of the food price. This extra money is kept by the person who served the food.
4. An antique furniture store pays $200 for a chair, adds 50% of that amount, and sells the chair for $300.
5. The normal price of a mattress is $600, but it is on sale for 10% off.
6. For any item you purchase in Texas, you pay an additional 6.25% of the item's price to the state government.

1. Tax
2. Commission
3. Discount
4. Markup
5. Tip or gratuity
6. Interest

(From Unit 4.3.2)

Exercise \(\PageIndex{7}\)

Clare drew this diagram to match the equation \(2x+16=50\), but she got the wrong solution as a result of using this diagram.

Figure \(\PageIndex{11}\)

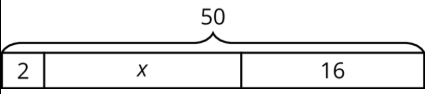
1. What value of \(x\) can be found using the diagram?
2. Show how to fix Clare's diagram to correctly match the equation.
3. Use th new diagram to find a correct value for \(x\).
4. Explain how the mistake Clare made when she drew her diagram.

(From Unit 6.1.3)