1.6: Solving Equations by Addition and Subtraction
- Page ID
- 22464
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Let’s start with the definition of a variable.
A variable is a symbol (usually a letter) that stands for a value that may vary
Next we follow with the definition of an equation.
An equation is a mathematical statement that equates two mathematical expressions.
The key difference between a mathematical expression and an equation is the presence of an an equals sign. So, for example,
2 + 3[5 − 4 · 2], x2 + 2x − 3, and x + 2y + 3
are mathematical expressions (two of which contain variables), while
3 + 2(7 − 3) = 11, x +3=4, and 3x = 9
are equations. Note that each of the equations contain an equals sign, but the expressions do not.
Next we have the definition of a solution of an equation.
A solution of an equation is a numerical value that satisfies the equation. That is, when the variable in the equation is replaced by the solution, a true statement results.
Show that 3 is a solution of the equation x + 8 = 11.
Solution
Substitute 3 for x in the given equation and simplify.
\[ \begin{array}{rlrl}{x+8} & {=11} & {} & { \textcolor{red}{ \text { The given equation. }}} \\ {3+8} & {=11} & {} & {\textcolor{red}{ \text { Substitute } 3 \text { for } x .}} \\ {11} & {=11} & {} & {\textcolor{red}{ \text { Simplify both sides. }}}\end{array}\nonumber \]
Since the left- and right-hand sides of the last line are equal, this shows that when 3 is substituted for x in the equation a true statement results. Therefore, 3 is a solution of the equation.
Show that 27 is a solution of the equation x − 12 = 15
Is 23 a solution of the equation 4 = y − 11?
Solution
Substitute 23 for y in the given equation and simplify.
\[ \begin{array}{ll}{4=y-11} & {\textcolor{red}{ \text { The given equation. }}} \\ {4=23-11} & {\textcolor{red}{ \text { Substitute } 23 \text { for } y}} \\ {4=12} & {\textcolor{red} {\text { Simplify both sides. }}}\end{array}\nonumber \]
Since the left- and right-hand sides of the last line are not equal, this shows that when 23 is substituted for y in the equation a false statement results. Therefore, 23 is not a solution of the equation.
Is 8 a solution of 5 = 12 − y?
- Answer
-
No.
Equivalent Equations
We start with the definition of equivalent equations.
Two equations are equivalent if they have the same solution set.
Are the equations x + 2 = 9 and x = 7 equivalent?
Solution
The number 7 is the only solution of the equation x + 2 = 9. Similarly, 7 is the only solution of the equation x = 7. Therefore x + 2 = 9 and Answer: No. x = 7 have the same solution sets and are equivalent.
Are the equations x = 4 and x + 8 = 3 equivalent?
- Answer
-
No.
Are the equations x2 = x and x = 1 equivalent?
Solution
By inspection, the equation x2 = x has two solutions, 0 and 1. On the other hand, the equation x = 1 has a single solution, namely 1. Hence, the equations x2 = x and x = 1 do not have the same solution sets and are not equivalent.
Are the equations x = 2 and x2 = 2x equivalent?
- Answer
-
No.
Operations that Produce Equivalent Equations
There are many operations that will produce equivalent operations. In this section we look at two: addition and subtraction.
Adding the same quantity to both sides of an equation does not change the solution set. That is, if
\[a = b,\nonumber \]
then adding c to both sides of the equation produces the equivalent equation
\[a + c = b + c.\nonumber \]
Let’s see if this works as advertised. Consider the equation x − 4=3. By inspection, 7 is the only solution of the equation. Now, let’s add 4 to both sides of the equation to see if the resulting equation is equivalent to x − 4 = 3.
\[ \begin{array}{rlrl}{x-4} & {=3} & {} & {\textcolor{red}{ \text{The given equation. }}} \\ {x-4+4} & {=3+4} & {} & {\textcolor{red}{ \text{Add 4 to both sides of the equation.} }} \\ {x} & {=7} & {} & {\textcolor{red}{ \text{Simplify both sides of the equation. }}}\end{array}\nonumber \]
The number 7 is the only solution of the equation x = 7. Thus, the equation x = 7 is equivalent to the original equation x − 4 = 3 (they have the same solutions).
Adding the same amount to both sides of an equation does not change its solutions.
It is also a fact that subtracting the same quantity from both sides of an equation produces an equivalent equation.
Subtracting the same quantity from both sides of an equation does not change the solution set. That is, if
\[a = b,\nonumber \]
then subtracting c from both sides of the equation produces the equivalent equation
\[a − c = b − c.\nonumber \]
Let’s also see if this works as advertised. Consider the equation
\[ x + 4 = 9.\nonumber \]
By inspection, 5 is the only solution of the equation. Now, let’s subtract 4 from both sides of the equation to see if the resulting equation is equivalent to x + 4 = 9.
\[ \begin{array}{rlrl}{x+4} & {=9} & {} & {\textcolor{red}{ \text { The given equation. }}} \\ {x+4-4} & {=9-4} & {} & {\textcolor{red}{ \text { Subtract 4 from both sides of the equation. }}} \\ {x} & {=5} & {} & {\textcolor{red}{ \text { Simplify both sides of the equation. }}}\end{array}\nonumber \]
The number 5 is the only solution of the equation \(x = 5\). Thus, the equation \(x = 5\) is equivalent to the original equation \(x + 4 = 9\) (they have the same solutions).
Subtracting the same amount from both sides of an equation does not change its solutions.
When solving equations, observe the following rules to neatly arrange your work:
1. One equation per line. This means that you should not arrange your work like this:
\[ x+3=7 \quad x+3-3=7-3 \quad x=4\nonumber \]
That’s three equations on a line. Rather, arrange your work one equation per line like this:
\[ \begin{aligned} x+3 &=7 \\ x+3-3 &=7-3 \\ x &=4 \end{aligned}\nonumber \]
2. Add and subtract inline. Don’t do this:
\[ \begin{array}{r} x -7 & = & 12 \\ +7 & & + 7 \\ \hline x & = & 19 \end{array}\nonumber \]
Instead, add 7 to both sides of the equation “inline.”
\[ \begin{aligned} x-7 &=12 \\ x-7+7 &=12+7 \\ x &=19 \end{aligned}\nonumber \]
Wrap and Unwrap
Suppose that you are wrapping a gift for your cousin. You perform the following steps in order.
- Put the gift paper on.
- Put the tape on.
- Put the decorative bow on.
When we give the wrapped gift to our cousin, he politely unwraps the present, “undoing” each of our three steps in inverse order.
- Take off the decorative bow.
- Take off the tape.
- Take off the gift paper.
This seemingly frivolous wrapping and unwrapping of a gift contains some deeply powerful mathematical ideas. Consider the mathematical expression \(x+ 4\). To evaluate this expression at a particular value of x, we would start with the given value of x, then
- Add 4.
Suppose we started with the number 7. If we add 4, we arrive at the following result: 11.
Now, how would we “unwrap” this result to return to our original number? We would start with our result, then
- Subtract 4.
That is, we would take our result from above, 11, then subtract 4, which returns us to our original number, namely 7.
Two extremely important observations:
The inverse of addition is subtraction. If we start with a number x and add a number a, then subtracting a from the result will return us to the original number x. In symbols,
\[x + a − a = x.\nonumber \]
The inverse of subtraction is addition. If we start with a number x and subtract a number a, then adding a to the result will return us to the original number x. In symbols,
\[x − a + a = x.\nonumber \]
Solve \(x − 8 = 10\) for x.
Solution
To undo the effects of subtracting 8, we add 8 to both sides of the equation.
\[ \begin{aligned} x-8=10 & \textcolor{red}{\text { Original equation. }} \\ x-8+8=10+8 & \textcolor{red}{ \text { Add 8 to both sides of the equation. }} \\ x=18 & \textcolor{red}{ \text { On the left, adding "undoes" the effect }} \\ & \textcolor{red}{ \text { of subtracting 8 and returns } x . \text { On the right, }} \\ & \textcolor{red}{10+8=18.} \end{aligned}\nonumber \]
Therefore, the solution of the equation is 18.
Check
To check, substitute the solution 18 into the original equation.
\[ \begin{aligned} x - 8 = 10 & \textcolor{red}{ \text{ Original equation. }} \\ 18 - 8 = 10 & \textcolor{red}{ \text{ Substitute 18 for} x. } \\ 10 = 10 & \textcolor{red}{ \text{ Simplify both sides. }} \end{aligned}\nonumber \]
The fact that the last line of our check is a true statement guarantees that 18 is a solution of x − 8 = 10.
Solve \(x + 5 = 12\) for x.
- Answer
-
7.
Solve \(11 = y + 5\) for y.
Solution
To undo the effects of adding 5, we subtract 5 from both sides of the equation.
\[ \begin{aligned} 11 = y + 5 & \textcolor{red}{ \text{ Original equation. }} \\ 1 - 5 = y + 5 - 5 & \textcolor{red}{ \text{ Subtract 5 from both sides of the equation. }} \\ 6 = y & \textcolor{red}{ \text{ On the right, subtracting "undoes" the effect }} \\ & \textcolor{red}{ \text{ of adding 5 and returns } y. \text{ On the left, }} \\ & \textcolor{red}{ 11 - 5 = 6. } \end{aligned}\nonumber \]
Therefore, the solution of the equation is 6.
Check
\[ \begin{aligned} 11 = y + 5 & \textcolor{red}{ \text{ Original equation. }} \\ 11 = 6 + 5 & \textcolor{red}{ \text{ Substitute 6 for } y.} \\ 11 = 11 & \textcolor{red}{ \text{ Simplify both sides. }} \end{aligned}\nonumber \]
The fact that the last line of our check is a true statement guarantees that 6 is a solution of 11 = y + 5.
Solve \(y - 8 = 11\) for y.
- Answer
-
\(y = 19.\)
Word Problems
The solution of a word problem must incorporate each of the following steps.
- Set up a Variable Dictionary. You must let your readers know what each variable in your problem represents. This can be accomplished in a number of ways:
- Statements such as “Let P represent the perimeter of the rectangle.”
- Labeling unknown values with variables in a table.
- Labeling unknown quantities in a sketch or diagram.
- Set up an Equation. Every solution to a word problem must include a carefully crafted equation that accurately describes the constraints in the problem statement.
- Solve the Equation. You must always solve the equation set up in the previous step.
- Answer the Question. This step is easily overlooked. For example, the problem might ask for Jane’s age, but your equation’s solution gives the age of Jane’s sister Liz. Make sure you answer the original question asked in the problem. Your solution should be written in a sentence with appropriate units.
- Look Back. It is important to note that this step does not imply that you should simply check your solution in your equation. After all, it’s possible that your equation incorrectly models the problem’s situation, so you could have a valid solution to an incorrect equation. The important question is: “Does your answer make sense based on the words in the original problem statement.”
Let's give these requirements a test drive.
Four more than a certain number is 12. Find the number.
Solution
In our solution, we will carefully address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We can satisfy this requirement by simply stating “Let x represent a certain number.”
2. Set up an Equation. “Four more than a certain number is 12” becomes
\[ \begin{aligned} \colorbox{cyan}{4} & \text{ more than } & \colorbox{cyan}{a certain number} & \text{ is } & \colorbox{cyan}{12} \\ 4 & + & x & = & 12 \end{aligned}\nonumber \]
3. Solve the Equation. To “undo” the addition, subtract 4 from both sides of the equation.
\[ \begin{aligned} 4 + x = 12 & \textcolor{red}{ \text{ Original equation.}} \\ 4 + x - 4 = 12 - 4 & \textcolor{red}{ \text{Subtract 4 from both sides of the equation. }} \\ x = 8 & \textcolor{red}{ \text{ On the left, subtracting 4 "undoes" the effect}} \\ & \textcolor{red}{ \text{ of adding 4 and returns } x. \text{ On the right, }} \\ & \textcolor{red}{12 - 4 = 8.} \end{aligned}\nonumber \]
4. Answer the Question. The number is 8.
5. Look Back. Does the solution 8 satisfy the words in the original problem? We were told that “four more than a certain number is 12.” Well, four more than 8 is 12, so our solution is correct.
12 more than a certain number is 19. Find the number.
- Answer
-
7
Amelie withdraws $125 from her savings account. Because of the withdrawal, the current balance in her account is now $1,200. What was the original balance in the account before the withdrawal?
Solution
In our solution, we will carefully address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We can satisfy this requirement by simply stating “Let B represent the original balance in Amelie’s account.”
2. Set up an Equation. We can describe the situation in words and symbols.
\[ \begin{aligned} \colorbox{cyan}{Original Balance} & \text{ minus } & \colorbox{ Amelie's Withdrawal } & \text{ is } & \colorbox{cyan}{ Current Balance } \\ B & - & 125 & = & 1200 \end{aligned}\nonumber \]
3. Solve the Equation. To “undo” the subtraction, add 125 to both sides of the equation.
\[ \begin{aligned} B - 125 = 1200 & \textcolor{red}{ \text{ Original equation. }} \\ B - 125 + 125 = 1200 + 125 & \textcolor{red}{ \text{Add 125 to both sides of the equation. }} \\ B = 1325 & \textcolor{red}{ \text{ On the left, adding 125 "undoes" the effect}} \\ & \textcolor{red}{ \text{ of subtracting 125 and returns } B. \text{ On the right, }} \\ & \textcolor{red}{ 1200 + 125 = 1325.} \end{aligned}\nonumber \]
4. Answer the Question. The original balance was $1,325.
5. Look Back. Does the solution $1,325 satisfy the words in the original problem? Note that if Amelie withdraws $125 from this balance, the new balance will be $1,200. Hence, the solution is correct.
Fred withdraws $230 from his account, lowering his balance to $3,500. What was his original balance?
- Answer
-
$3730
The perimeter of a triangle is 114 feet. Two sides of the triangle measure 30 feet and 40 feet, respectively. Find the measure of the third side of the triangle.
Solution
In our solution, we will carefully address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. When geometry is involved, we can create our variable dictionary by labeling a carefully constructed diagram. With this thought in mind, we draw a triangle, then label its known and unknown sides and its perimeter.
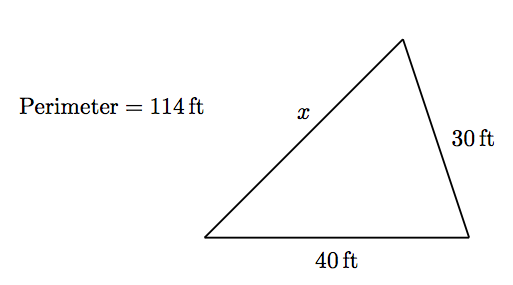
The figure makes it clear that x represents the length of the unknown side of the triangle. The figure also summarizes information needed for the solution. 2. Set up an equation. We know that the perimeter of a triangle is found by finding the sum of its three sides; in words and symbols,
\[ \begin{aligned} \colorbox{cyan}{ Perimeter } & \text{ is } & \colorbox{cyan}{ First Side } & \text{ plus } & \colorbox{cyan}{ Second Side } & \text{ plus } & \colorbox{cyan}{ Third Side } \\ 114 & = & x & + & 30 & + & 40 \end{aligned}\nonumber \]
Simplify the right-hand side by adding 30 and 40; i.e., \(30 + 40 = 70\).
\[ 114 = x + 70\nonumber \]
3. Solve the Equation. To “undo” adding 70, subtract 70 from both sides of the equation.
\[ \begin{aligned} 114 = x + 70 & \textcolor{red}{ \text{ Our equation. }} \\ 114 - 70 = x + 70 - 70 & \textcolor{red}{ \text{ Subtract 70 from both sides. }} \\ 44 = x & \textcolor{red}{ \text{ On the right, subtracting 70 "undoes" the effect}} \\ & \textcolor{red}{ \text{of adding 70 and returns to } x. \text{ On the left,}} \\ & \textcolor{red}{ 114 - 70 = 44.} \end{aligned}\nonumber \]
4. Answer the Question. The unknown side of the triangle is 44 feet.
5. Look Back. Does the solution 44 feet satisfy the words of the original problem? We were told that the perimeter is 114 feet and two of the sides have length 30 feet and 40 feet respectively. We found that the third side has length 44 feet. Now, adding the three sides, 30+ 40+ 44 = 114, which equals the given perimeter of 114 feet. The answer works!
The perimeter of a quadrilateral is 200 meters. If three of the sides measure 20, 40, and 60 meters, what is the length of the fourth side.
- Answer
-
80 meters
Exercises
In Exercises 1-12, which of the numbers following the given equation are solutions of the given equation? Support your response with work similar to that shown in Examples 1 and 2.
1. x − 4 = 6; 10, 17, 13, 11
2. x − 9 = 7; 17, 23, 19, 16
3. x + 2 = 6; 5, 11, 7, 4
4. x + 3 = 9; 6, 9, 7, 13
5. x + 2 = 3; 8, 1, 4, 2
6. x + 2 = 5; 10, 3, 6, 4
7. x − 4 = 7; 12, 11, 18, 14
8. x − 6 = 7; 13, 16, 20, 14
9. x + 3 = 4; 8, 4, 2, 1
10. x + 5 = 9; 5, 11, 7, 4
11. x − 6 = 8; 17, 21, 14, 15
12. x − 2 = 9; 11, 14, 12, 18
In Exercises 13-52, solve the given equation for x.
13. x +5=6
14. x + 6 = 19
15. 5=4+ x
16. 10 = 8 + x
17. 13 + x = 17
18. 7+ x = 15
19. 9+ x = 10
20. 14 + x = 17
21. 19 = x − 3
22. 2= x − 11
23. x − 18 = 1
24. x − 20 = 8
25. x − 3 = 11
26. x − 17 = 18
27. 2+ x = 4
28. 1+ x = 16
29. x − 14 = 12
30. x − 1 = 17
31. x +2=8
32. x + 11 = 14
33. 11 + x = 17
34. 11 + x = 18
35. x + 13 = 17
36. x + 1 = 16
37. 20 = 3 + x
38. 9=3+ x
39. 20 = 8 + x
40. 10 = 3 + x
41. 3= x − 20
42. 13 = x − 15
43. x + 16 = 17
44. x + 6 = 12
45. 5= x − 6
46. 10 = x − 7
47. 18 = x − 6
48. 14 = x − 4
49. 18 = 13 + x
50. 17 = 5 + x
51. x − 9 = 15
52. x − 11 = 17
53. 12 less than a certain number is 19. Find the number.
54. 19 less than a certain number is 1. Find the number.
55. A triangle has a perimeter of 65 feet. It also has two sides measuring 19 feet and 17 feet, respectively. Find the length of the third side of the triangle.
56. A triangle has a perimeter of 55 feet. It also has two sides measuring 14 feet and 13 feet, respectively. Find the length of the third side of the triangle.
57. Burt makes a deposit to an account having a balance of $1900. After the deposit, the new balance in the account is $8050. Find the amount of the deposit.
58. Dave makes a deposit to an account having a balance of $3500. After the deposit, the new balance in the account is $4600. Find the amount of the deposit.
59. 8 more than a certain number is 18. Find the number.
60. 3 more than a certain number is 19. Find the number.
61. Michelle withdraws a $120 from her bank account. As a result, the new account balance is $1000. Find the account balance before the withdrawal.
62. Mercy withdraws a $430 from her bank account. As a result, the new account balance is $1200. Find the account balance before the withdrawal.
63. Foreclosures. Between January and March last year, 650,000 homes received a foreclosure notice. Between the first three months of this year, there were 804,000 foreclosure notices. What was the increase in home foreclosure notices? Associated Press Times-Standard 4/22/09
64. Home Price. According to the Humboldt State University Economics Department’s Humboldt Economic Index, the median home price in the US fell $1500 over the last month to $265,000. What was the median home price before the price drop?
65. Unmanned Areal Vehicle. Northrup Grumman’s Global Hawk unmanned drone can fly at 65,000 feet, 40,000 feet higher than NASA’s Ikhana unmanned aircraft. How high can the Ikhana fly?
66. Tribal Land. The Yurok Tribe has the option to purchase 47,000 acres in order to increase its ancestral territory. The first phase would include 22,500 acres in the Cappel and Pecman watersheds. The second phase plans for acreage in the Blue Creek area. How many acres could be purchased in the second phase? Times-Standard 4/15/09
Answers
1. 10
3. 4
5. 1
7. 11
9. 1
11. 14
13. 1
15. 1
17. 4
19. 1
21. 22
23. 19
25. 14
27. 2
29. 26
31. 6
33. 6
35. 4
37. 17
39. 12
41. 23
43. 1
45. 11
47. 24
49. 5
51. 24
53. 31
55. 29
57. $6150
59. 10
61. $1120
63. 154,000
65. 25,000 feet


