1.7: Solving Equations by Multiplication and Division
- Page ID
- 23213
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Section 1.6, we stated that two equations that have the same solutions are equivalent. Furthermore, we saw that adding the same number to both sides of an equation produced an equivalent equation. Similarly, subtracting the same the number from both sides of an equation also produces an equivalent equation. We can make similar statements for multiplication and division.
Multiplying both sides of an equation by the same quantity does not change the solution set. That is, if
\[ a = b\nonumber \]
then multiplying both sides of the equation by c produces the equivalent equation
\[ a \cdot c = b \cdot c\nonumber \]
provided c ≠ 0.
A similar statement can be made about division.
Dividing both sides of an equation by the same quantity does not change the solution set. That is, if
\[ a = b\nonumber \]
then dividing both sides of the equation by c produces the equivalent equation
\[ \frac{a}{c} = \frac{b}{c},\nonumber \]
provided c ≠ 0.
In Section 1.6, we saw that addition and subtraction were inverse operations. If you start with a number, add 4 and subtract 4, you are back to the original number. This concept also works for multiplication and division.
Two extremely important observations:
The inverse of multiplication is division. If we start with a number x and multiply by a number a, then dividing the result by the number a returns us to the original number x. In symbols,
\[ \frac{a \cdot x}{a} = x.\nonumber \]
The inverse of division is multiplication. If we start with a number x and divide by a number a, then multiplying the result by the number a returns us to the original number x. In symbols,
\[ a \cdot \frac{x}{a} = x.\nonumber \]
Let's put these ideas to work.
Solve the equation 3x = 24 for x.
Solution
To undo the effects of multiplying by 3, we divide both sides of the equation by 3.
\[ \begin{aligned} 3x= 24 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{3x}{3} = \frac{24}{3} ~ & \textcolor{red}{ \text{Divide both sides of the equation by 3.}} \\ x = 8 ~ & \textcolor{red}{ \text{ On the left, dividing by 3 "undoes" the effect}} \\ ~ & \textcolor{red}{ \text{ of multiplying by 3 and returns to } x. \text{ On the right,}} \\ ~ & \textcolor{red}{ 24/3 = 8.} \end{aligned}\nonumber \]
To check, substitute the solution 8 into the original equation.
\[ \begin{aligned} 3x = 24 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3(8) = 24 ~ & \textcolor{red}{ \text{Substitute 8 for } x.} \\ 24 = 24 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
That fact that the last line of our check is a true statement guarantees that 8 is a solution of 3x = 24.
Solve for x: 5x = 120.
- Answer
-
24
Solve the following equation for x.
\[ \frac{x}{7} = 12\nonumber \]
Solution
To undo the effects of dividing by 7, we multiply both sides of the equation by 7.
\[ \begin{aligned} \frac{x}{7} = 12 ~ & \textcolor{red}{ \text{Original equation.}} \\ \frac{84}{7} = 12 ~ & \textcolor{red}{ \text{ Multiply both sides of the equation by 7.}} \\ x = 84 ~ & \textcolor{red}{ \text{ On the left, multiplying by 7 "undoes" the effect}} \\ ~ & \textcolor{red}{ \text{ of dividing by 7 and returns to } x. \text{ On the right,}} \\ ~ & \textcolor{red}{ 7 \cdot 12 = 84.} \end{aligned}\nonumber \]
To check, substitute the solution 84 into the original equation.
\[ \begin{aligned} \frac{x}{7} = 12 & \textcolor{red}{ \text{ Original equation.}} \\ \frac{84}{7} = 12 ~ & \textcolor{red}{ \text{ Substitute 84 for } x.} \\ 12 = 12 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
That fact that the last line of our check is a true statement guarantees that 84 is a solution of x/7 = 12.
Solve for x: x/2 = 19
- Answer
-
38
Word Problems
In Section 1.6 we introduced Requirements for Word Problem Solutions. Those requirements will be strictly adhered to in this section.
Fifteen times a certain number is 45. Find the unknown number.
Solution
In our solution, we will carefully address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We can satisfy this requirement by simply stating “Let x represent a certain number.”
2. Set up an equation. “Fifteen times a certain number is 45” becomes
\[ \begin{array}{c c c c} \colorbox{cyan}{15} & \text{times} & \colorbox{cyan}{a certain number} & \text{is} & \colorbox{cyan}{45} \\ 15 & \cdot & x & = & 45 \end{array}\nonumber \]
3. Solve the Equation. To “undo” the multiplication by 15, divide both sides of the equation by 15.
\[ \begin{aligned} 15x = 45 ~ & \textcolor{red}{ \text{ Original equation. Write 15 } \cdot x \text{ as 15}x} \\ \frac{15x}{15} = \frac{45}{15} ~& \textcolor{red}{ \text{ Divide both sides of the equation by 15.}} \\ x = 3 ~ & \textcolor{red}{ \text{ On the left, dividing by 15 "undoes" the effect}} \\ ~ & \textcolor{red}{ \text{ of multiplying by 15 and returns to } x. \text{ On the right,}} \\ ~ & \textcolor{red}{45/15 = 3.} \end{aligned}\nonumber \]
4. Answer the Question. The unknown number is 3.
5. Look Back. Does the solution 3 satisfy the words of the original problem? We were told that “15 times a certain number is 45.” Well, 15 times 3 is 45, so our solution is correct.
Seven times a certain number is one hundred five. Find the unknown number.
- Answer
-
15
The area of a rectangle is 120 square feet. If the length of the rectangle is 12 feet, find the width of the rectangle.
Solution
In our solution, we will carefully address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. When geometry is involved, we can create our variable dictionary by labeling a carefully constructed diagram. With this thought in mind, we draw a rectangle, then label its length, width, and area.
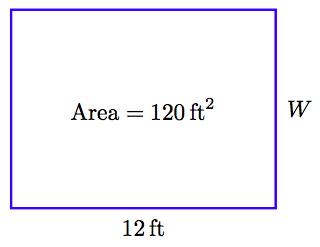
The figure makes it clear that W represents the width of the rectangle. The figure also summarizes information needed for the solution.
2. Set up an equation. We know that the area of a rectangle is found by multiplying its length and width; in symbols,
\[ A = LW.\nonumber \]
We’re given the area is A = 120 ft2 and the length is L = 12 ft. Substitute these numbers into the area formula (1.1) to get
\[120 = 12W.\nonumber \]
3. Solve the Equation. To “undo” the multiplication by 12, divide both sides of the equation by 12.
\[ \begin{aligned} 120 = 12W ~ & \textcolor{red}{ \text{ Our equation.}} \\ \frac{120}{12} = \frac{12W}{12} ~ & \textcolor{red}{ \text{ Divide both sides of the equation by 12.}} \\ 10 = W ~ & \textcolor{red}{ \text{ On the right, dividing by 12 "undoes" the effect}} \\ ~ & \textcolor{red}{ \text{ of multiplying by 12 and returns to } W. \text{ On the left,}} \\ ~ & \textcolor{red}{120/12 = 10.} \end{aligned}\nonumber \]
4. Answer the Question. The width is 10 feet.
5. Look Back. Does the found width satisfy the words of the original problem? We were told that the area is 120 square feet and the length is 12 feet. The area is found by multiplying the length and width, which gives us 12 feet times 10 feet, or 120 square feet. The answer works!
The area of a rectangle is 3,500 square meters. If the width is 50 meters, find the length.
- Answer
-
70 meters
A class of 23 students averaged 76 points on an exam. How many total points were accumulated by the class as a whole?
Solution
In our solution, we will carefully address each step of the Requirements for Word Problem Solutions. 1. Set up a Variable Dictionary. We can set up our variable dictionary by simply stating “Let T represent the total points accumulated by the class.” 2. Set up an equation. To find the average score on the exam, take the total points accumulated by the class, then divide by the number of students in the class. In words and symbols,
\[ \begin{array}{c c c c c} \colorbox{cyan}{Total Points} & \text{divided by} & \colorbox{cyan}{ Number of Students} & \text{equals} & \text{Average Score} \\ T & \div & 23 & = & 76 \end{array}\nonumber \]
An equivalent representation is
\[ \frac{T}{23} = 76.\nonumber \]
3. Solve the Equation. To “undo” the division by 23, multiply both sides of the equation by 23.
\[ \begin{aligned} \frac{T}{23} = 76 & \textcolor{red}{ \text{ Our equation.}} \\ 23 \cdot \frac{T}{23} = 76 \cdot 23 & \textcolor{red}{ \text{ Multiply both sides of the equation by 23.}} \\ T = 1748 & \textcolor{red}{ \text{ On the left, multiplying by 23 "undoes" the effect}} \\ ~ & \textcolor{red}{ \text{ of dividing by 23 and returns to } T. \text{ On the right, }} \\ ~ & \textcolor{red}{76 \cdot 23 = 1748.} \end{aligned}\nonumber \]
4. Answer the Question. The total points accumulated by the class on the exam is 1,748.
5. Look Back. Does the solution 1,748 satisfy the words of the original problem? To find the average on the exam, divide the total points 1,748 by 23, the number of students in the class. Note that this gives an average score of 1748 ÷ 23 = 76. The answer works!
A class of 30 students averaged 75 points on an exam. How many total points were accumulated by the class as a whole?
- Answer
-
2,250
Exercises
In Exercises 1-12, which of the numbers following the given equation are solutions of the given equation?
1. \(\frac{x}{6} = 4\); 24, 25, 27, 31
2. \(\frac{x}{7} = 6\); 49, 42, 43, 45
3. \(\frac{x}{2} = 3\); 6, 9, 13, 7
4. \(\frac{x}{9} = 5\); 45, 46, 48, 52
5. \(5x = 10\); 9, 2, 3, 5
6. \(4x = 36\); 12, 16, 9, 10
7. \(5x = 25\); 5, 6, 8, 12
8. \(3x = 3\); 1, 8, 4, 2
9. \(2x = 2\); 4, 8, 1, 2
10. \(3x = 6\); 2, 9, 5, 3
11. \(\frac{x}{8} = 7\); 57, 59, 63, 56
12. \(\frac{x}{3} = 7\); 24, 21, 28, 22
In Exercises 13-36, solve the given equation for x.
13. \(\frac{x}{6} = 7\)
14. \(\frac{x}{8} = 6\)
15. \(2x = 16\)
16. \(2x = 10\)
17. \(2x = 18\)
18. \(2x = 0\)
19. \(4x = 24\)
20. \(2x = 4\)
21. \( \frac{x}{4} = 9\)
22. \( \frac{x}{5} = 6\)
23. \(5x = 5\)
24. \(3x = 15\)
25. \(5x = 30\)
26. \(4x = 28\)
27. \( \frac{x}{3} = 4\)
28. \( \frac{x}{9} = 4\)
29. \( \frac{x}{8} = 9\)
30. \( \frac{x}{8} = 2\)
31. \( \frac{x}{7} = 8\)
32. \( \frac{x}{4} = 6\)
33. \(2x = 8\)
34. \(3x = 9\)
35. \( \frac{x}{8} = 5\)
36. \(\frac{x}{5} = 4\)
37. The price of one bookcase is $370. A charitable organization purchases an unknown number of bookcases and the total price of the purchase is $4,810. Find the number of bookcases purchased.
38. The price of one computer is $330. A charitable organization purchases an unknown number of computers and the total price of the purchase is $3,300. Find the number of computers purchased.
39. When an unknown number is divided by 3, the result is 2. Find the unknown number.
40. When an unknown number is divided by 8, the result is 3. Find the unknown number.
41. A class of 29 students averaged 80 points on an exam. How many total points were accumulated by the class as a whole?
42. A class of 44 students averaged 87 points on an exam. How many total points were accumulated by the class as a whole?
43. When an unknown number is divided by 9, the result is 5. Find the unknown number.
44. When an unknown number is divided by 9, the result is 2. Find the unknown number.
45. The area of a rectangle is 16 square cm. If the length of the rectangle is 2 cm, find the width of the rectangle.
46. The area of a rectangle is 77 square ft. If the length of the rectangle is 7 ft, find the width of the rectangle.
47. The area of a rectangle is 56 square cm. If the length of the rectangle is 8 cm, find the width of the rectangle.
48. The area of a rectangle is 55 square cm. If the length of the rectangle is 5 cm, find the width of the rectangle.
49. The price of one stereo is $430. A charitable organization purchases an unknown number of stereos and the total price of the purchase is $6,020. Find the number of stereos purchased.
50. The price of one computer is $490. A charitable organization purchases an unknown number of computers and the total price of the purchase is $5,880. Find the number of computers purchased.
51. A class of 35 students averaged 74 points on an exam. How many total points were accumulated by the class as a whole?
52. A class of 44 students averaged 88 points on an exam. How many total points were accumulated by the class as a whole?
53. 5 times an unknown number is 20. Find the unknown number.
54. 5 times an unknown number is 35. Find the unknown number.
55. 3 times an unknown number is 21. Find the unknown number.
56. 2 times an unknown number is 10. Find the unknown number.
Answers
1. 24
3. 6
5. 2
7. 5
9. 1
11. 56
13. 42
15. 8
17. 9
19. 6
21. 36
23. 1
25. 6
27. 12
29. 72
31. 56
33. 4
35. 40
37. 13
39. 6
41. 2,320
43. 45
45. 8 cm
47. 7 cm
49. 14
51. 2,590
53. 4
55. 7


