3.2: Evaluating Algebraic Expressions
- Page ID
- 22474
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we will evaluate algebraic expressions for given values of the variables contained in the expressions. Here are some simple tips to help you be successful.
Tips for Evaluating Algebraic Expressions
- Replace all occurrences of variables in the expression with open parentheses. Leave room between the parentheses to substitute the given value of the variable.
- Substitute the given values of variables in the open parentheses prepared in the first step.
- Evaluate the resulting expression according to the Rules Guiding Order of Operations.
Let's begin with an example.
Evaluate the expression \(x^2 − 2xy + y^2\) at \(x = −3\) and \(y = 2\).
Solution
Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression x2 − 2xy + y2 with open parentheses.
\[ x^2 -2xy + y^2 = ( ~ )^2 -2(~)(~) + ( ~ )^2 \nonumber\nonumber \]
Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.
\[ \begin{aligned} x^2 -2xy + y^2 ~ & \textcolor{red}{ \text{ Original expression.}} \\ =( \textcolor{red}{-3} )^2 -2 ( \textcolor{red}{-3})( \textcolor{red}{2}) + (\textcolor{red}{2})^2 ~ & \textcolor{red}{ \text{ Substitute } -3 \text{ for } x \text{and 2 for }y.} \\ =9-2(-3)(2)+4 ~ & \textcolor{red}{ \text{ Evaluate exponents first.}} \\ = 9-(-6)(2)+4 ~ & \textcolor{red}{ \text{ Left to right, multiply } 2(-3)=-6.} \\ =9-(-12)+4 ~ & \textcolor{red}{ \text{ Left to right, multiply: } (-6)(2) = -12.} \\ = 9 + 12 + 4 ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = 25 ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
If x = −2 and y = −1, evaluate x3 − y3.
- Answer
-
−7
Evaluate the expression (a − b)2 If a = 3 and b = −5, at a = 3 and b = −5.
Solution
Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression (a − b)2 with open parentheses.
\[ (a-b)^2 = (()-())^2\nonumber \]
Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.
\[ \begin{aligned} (a-b)^2 = (( \textcolor{red}{3})-( \textcolor{red}{-5}))^2 ~ & \textcolor{red}{ \text{ Substitute 3 for } a \text{ and } -5 \text{ for } b.} \\ = (3+5)^2 ~ & \textcolor{red}{ \text{ Add the opposite: } (3)-(-5)=3+5} \\ = 8^2 ~ & \textcolor{red}{ \text{ Simplify inside parentheses: } 3+5 = 8} \\ =64 ~ & \textcolor{red}{ \text{ Evaluate exponent: } 8^2 = 64} \end{aligned}\nonumber \]
If a = 3 and b = −5, evaluate a2 − b2.
- Answer
-
−16
Evaluate the expression |a|−|b| at a = 5 and b = −7.
Solution
Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression |a|−|b| with open parentheses.
\[ |a| - |b| = |( ~ )| - |( ~ )|\nonumber \]
Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.
\[ \begin{aligned} |a| - |b| = |( \textcolor{red}{5} )| = |( \textcolor{red}{-7})| ~ & \textcolor{red}{ \text{ Substitute 5 for } a \text{ and } -7 \text{ for } b.} \\ = 5 - 7 ~ & \textcolor{red}{ \text{ Absolute values first: } |(5)| = 5 \text{ and } |(-7)|=7|} \\ =5+(-7) ~ & \textcolor{red}{ \text{ Add the opposites: } 5 - 7 = 5+(-7).} \\ =-2 ~ & \textcolor{red}{ \text{ Add: } 5+(-7)=-2.} \end{aligned}\nonumber \]
If a = 5 and b = −7, evaluate 2|a| − 3|b|.
- Answer
-
−11
Evaluate the expression |a − b| at a = 5 and b = −7.
Solution
Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression |a − b| with open parentheses.
\[ |a-b| = |(~)-(~)|\nonumber \]
Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.
\[ \begin{aligned} |a-b| = |( \textcolor{red}{5})-( \textcolor{red}{-7})| ~ & \textcolor{red}{ \text{ Substitute 5 for } a \text{ and } -7 \text{ for } b.} \\ = |5+7| ~ & \textcolor{red}{ \text{ Add the opposite: } 5-(-7)=5+7.} \\ =|12| ~ & \textcolor{red}{ \text{ Add: } 5+7=12.} \\ =12 ~ & \textcolor{red}{ \text{ Take the absolute value: } |12| = 12.} \end{aligned}\nonumber \]
If a = 5 and b = −7, evaluate |2a − 3b|.
- Answer
-
31
Evaluate the expression
\[ \frac{ad-bc}{a+b}\nonumber \]
at a = 5, b = −3, c = 2, and d = −4.
Solution
Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression with open parentheses.
\[ \frac{ad-bc}{a+b} = \frac{(~)(~)-(~)(~)}{(~)+(~)}\nonumber \]
Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.
\[ \begin{aligned} \frac{ad-bc}{a+b} = \frac{( \textcolor{red}{5}) -( \textcolor{red}{-3}) ( \textcolor{red}{2})}{( \textcolor{red}{5}) + ( \textcolor{red}{-3})} ~ & \textcolor{red}{ \text{ Substitute: } 5 \text{ for } a,~ -3 \text{ for } b,~ 2 \text{ for } c,~ -4 \text{ for } d.} \\ = \frac{-20-(-6)}{2} ~ & \begin{aligned} \textcolor{red}{ \text{ Numerator: } (5)(=4)=-20,~ (-3)(2) = -6.} \\ \textcolor{red}{ \text{ Denominator: } 5+(-3)=2.} \end{aligned} \\ = \frac{-20+6}{2} ~ & \textcolor{red}{ \text{ Numerator: Add the opposite.}} \\ = \frac{-14}{2} ~ & \textcolor{red}{ \text{ Numerator: } -20+6=-14.} \\ = -7 ~ & \textcolor{red}{ \text{Divide.}} \end{aligned}\nonumber \]
If a = −7, b = −3, c = −15, 15, and d = −14, evaluate:
\[\frac{a^2+b^2}{c+d}\nonumber \]
- Answer
-
−2
Pictured below is a rectangular prism.
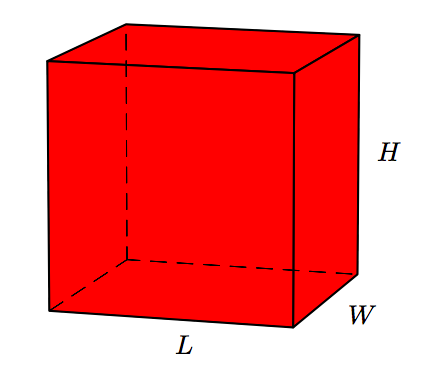
The volume of the rectangular prism is given by the formula
\[V=LWH,\nonumber \]
where L is the length, W is the width, and H is the height of the rectangular prism. Find the volume of a rectangular prism having length 12 feet, width 4 feet, and height 6 feet.
Solution
Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of of L, W, and H in the formula
\[ V = LWH\nonumber \]
with open parentheses.
\[V = (~)(~)(~)\nonumber \]
Next, substitute 12 ft for L, 4 ft for W, and 6 ft for H and simplify.
\[ \begin{aligned} V = (12 \text{ft})(4 \text{ft})(6 \text{ft}) \\ = 288 \text{ft}^3 \end{aligned}\nonumber \]
Hence, the volume of the rectangular prism is 288 cubic feet.
The surface area of the prism pictured in this example is given by the following formula:
\[S = 2(W H + LH + LW) \nonumber \]
If L = 12, W = 4, and H = 6 feet, respectively, calculate the surface area.
- Answer
-
288 square feet
Exercises
In Exercises 1-12, evaluate the expression at the given value of x.
1. −3x2 − 6x + 3 at x = 7
2. 7x2 − 7x + 1 at x = −8
3. −6x − 6 at x = 3
4. 6x − 1 at x = −10
5. 5x2 + 2x + 4 at x = −1
6. 4x2 − 9x + 4 at x = −3
7. −9x − 5 at x = −2
8. −9x + 12 at x = 5
9. 4x2 + 2x + 6 at x = −6
10. −3x2 + 7x + 4 at x = −7
11. 12x + 10 at x = −12
12. −6x + 7 at x = 11
In Exercises 13-28, evaluate the expression at the given values of x and y.
13. |x|−|y| at x = −5 and y = 4
14. |x|−|y| at x = −1 and y = −2
15. −5x2 + 2y2 at x = 4 and y = 2
16. −5x2 − 4y2 at x = −2 and y = −5
17. |x|−|y| at x = 0 and y = 2
18. |x|−|y| at x = −2 and y = 0
19. |x − y| at x = 4 and y = 5
20. |x − y| at x = −1 and y = −4
21. 5x2 − 4xy + 3y2 at x = 1 and y = −4
22. 3x2 + 5xy + 3y2 at x = 2 and y = −1
23. |x − y| at x = 4 and y = 4
24. |x − y| at x = 3 and y = −5
25. −5x2 − 3xy + 5y2 at x = −1 and y = −2
26. 3x2 − 2xy − 5y2 at x = 2 and y = 5
27. 5x2 + 4y2 at x = −2 and y = −2
28. −4x2 + 2y2 at x = 4 and y = −5
In Exercises 29-40, evaluate the expression at the given value of x.
29. \( \frac{9+9x}{−x}\) at x = −3
30. \( \frac{9 − 2x}{−x}\) at x = −1
31. \(\frac{−8x + 9}{−9 + x}\) at x = 10
32. \(\frac{2x + 4}{1 + x}\) at x = 0
33. \(\frac{−4+9x}{7x}\) at x = 2
34. \(\frac{−1 − 9x}{x}\) at x = −1
35. \(\frac{−12 − 7x}{x}\) at x = −1
36. \(\frac{12 + 11x}{3x}\) at x = −6
37. \(\frac{6x − 10}{5}\) + x at x = −6
38. \(\frac{11x + 11}{−4}\) + x at x = 5
39. \(\frac{10x + 11}{5}\) + x at x = −4
40. \(\frac{6x + 12}{−3}\) + x at x = 2
41. The formula
\[d=16t^2\nonumber \]
gives the distance (in feet) that an object falls from rest in terms of the time t that has elapsed since its release. Find the distance d (in feet) that an object falls in t = 4 seconds.
42. The formula
\[d = 16t^2\nonumber \]
gives the distance (in feet) that an object falls from rest in terms of the time t that has elapsed since its release. Find the distance d (in feet) that an object falls in t = 24 seconds.
43. The formula
\[C = \frac{5(F − 32)}{9}\nonumber \]
gives the Celcius temperature C in terms of the Fahrenheit temperature F. Use the formula to find the Celsius temperature (◦ C) if the Fahrenheit temperature is F = 230◦ F.
44. The formula
\[C = \frac{5(F − 32)}{9}\nonumber \]
gives the Celcius temperature C in terms of the Fahrenheit temperature F. Use the formula to find the Celsius temperature (◦C) if the Fahrenheit temperature is F = 95 ◦F.
45. The Kelvin scale of temperature is used in chemistry and physics. Absolute zero occurs at 0◦ K, the temperature at which molecules have zero kinetic energy. Water freezes at 273◦ K and boils at K = 373◦ K. To change Kelvin temperature to Fahrenheit temperature, we use the formula
\[F = \frac{9(K − 273)}{5} + 32.\nonumber \]
Use the formula to change 28◦ K to Fahrenheit.
46. The Kelvin scale of temperature is used in chemistry and physics. Absolute zero occurs at 0◦ K, the temperature at which molecules have zero kinetic energy. Water freezes at 273◦ K and boils at K = 373◦ K. To change Kelvin temperature to Fahrenheit temperature, we use the formula
\[F = \frac{9(K − 273)}{5} + 32.\nonumber \]
Use the formula to change 248◦ K to Fahrenheit.
47. A ball is thrown vertically upward. Its velocity t seconds after its release is given by the formula
\[v = v0 − gt,\nonumber \]
where v0 is its initial velocity, g is the acceleration due to gravity, and v is the velocity of the ball at time t. The acceleration due to gravity is g = 32 feet per second per second. If the initial velocity of the ball is v0 = 272 feet per second, find the speed of the ball after t = 6 seconds.
48. A ball is thrown vertically upward. Its velocity t seconds after its release is given by the formula
\[v = v_0 − gt,\nonumber \]
where v0 is its initial velocity, g is the acceleration due to gravity, and v is the velocity of the ball at time t. The acceleration due to gravity is g = 32 feet per second per second. If the initial velocity of the ball is v0 = 470 feet per second, find the speed of the ball after t = 4 seconds.
49. Even numbers. Evaluate the expression 2n for the following values:
i) n = 1
ii) n = 2
iii) n = 3
iv) n = −4
v) n = −5
vi) Is the result always an even number? Explain.
50. Odd numbers. Evaluate the expression 2n + 1 for the following values:
i) n = 1
ii) n = 2
iii) n = 3
iv) n = −4
v) n = −5
vi) Is the result always an odd number? Explain.
Answers
1. −186
3. −24
5. 7
7. 13
9. 138
11. −134
13. 1
15. −72
17. −2
19. 1
21. 69
23. 0
25. 9
27. 36
29. −6
31. −71
33. 1
35. 5
37. 46
39. −29
41. 256 feet
43. 110 degrees
45. −409◦ F
47. 80 feet per second
49.
i) 2
ii) 4
iii) 6
iv) −8
v) −10
vi) Yes, the result will always be an even number because 2 will always be a factor of the product 2n.


