4.3: Multiplying Fractions
- Page ID
- 22481
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Consider the image in Figure 4.5, where the vertical lines divide the rectangular region into three equal pieces. If we shade one of the three equal pieces, the shaded area represents 1/3 of the whole rectangular region.

We’d like to visualize taking 1/2 of 1/3. To do that, we draw an additional horizontal line which divides the shaded region in half horizontally. This is shown in Figure 4.6. The shaded region that represented 1/3 is now divided into two smaller rectangular regions, one of which is shaded with a different color. This region represents 1/2 of 1/3.

Next, extend the horizontal line the full width of the rectangular region, as shown in Figure 4.7.

Note that drawing the horizontal line, coupled with the three original vertical lines, has succeeded in dividing the full rectangular region into six smaller but equal pieces, only one of which (the one representing 1/2 of 1/3) is shaded in a new color. Hence, this newly shaded piece represents 1/6 of the whole region. The conclusion of our visual argument is the fact that 1/2 of 1/3 equals 1/6. In symbols,
\[ \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6} .\nonumber \]
Create a visual argument showing that 1/3 of 2/5 is 2/15.
Solution
First, divide a rectangular region into five equal pieces and shade two of them. This represents the fraction 2/5.
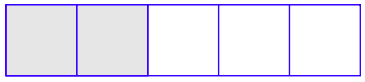
Next, draw two horizontal lines that divide the shaded region into three equal pieces and shade 1 of the three equal pieces. This represents taking 1/3 of 2/5.
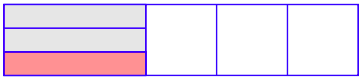
Next, extend the horizontal lines the full width of the region and return the original vertical line from the first image.
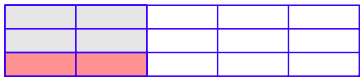
Note that the three horizontal lines, coupled with the five original vertical lines, have succeeded in dividing the whole region into 15 smaller but equal pieces, only two of which (the ones representing 1/3 of 2/5) are shaded in the new color. Hence, this newly shaded piece represents 2/15 of the whole region. The conclusion of this visual argument is the fact that 1/3 of 2/5 equals 2/15. In symbols,
\[ \frac{1}{3} \cdot \frac{2}{5} = \frac{2}{15}.\nonumber \]
Create a visual argument showing that 1/2 of 1/4 is 1/8.
- Answer
-
Diagram:

Multiplication Rule
In Figure 4.7, we saw that 1/2 of 1/3 equals 1/6. Note what happens when we multiply the numerators and multiply the denominators of the fractions 1/2 and 1/3.
\[ \begin{aligned} \frac{1}{2} \cdot \frac{1}{3} = \frac{1 \cdot 1}{2 \cdot 3} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{1}{6} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]
We get 1/6!
Could this be coincidence or luck? Let’s try that again with the fractions from Example 1, where we saw that 1/3 of 2/5 equals 2/15. Again, multiply the numerators and denominators of 1/3 and 2/5.
\[ \begin{aligned} \frac{1}{3} \cdot \frac{2}{5} = \frac{1 \cdot 2}{3 \cdot 5} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{2}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]
Again, we get 2/15!
These two examples motivate the following definition.
To find the product of the fractions a/b and c/d, multiply their numerators and denominators. In symbols,
\[ \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d}\nonumber \]
Multiply 1/5 and 7/9.
Solution
Multiply numerators and multiply denominators.
\[ \begin{aligned} \frac{1}{5} \cdot \frac{7}{9} = \frac{1 \cdot 7}{5 \cdot 9} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{7}{45} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]
Multiply:
\[ \frac{1}{3} \cdot \frac{2}{5}\nonumber \]
- Answer
-
Multiply: \( \frac{6}{15}\)
Find the product of −2/3 and 7/9.
Solution
The usual rules of signs apply to products. Unlike signs yield a negative result.
\[ \begin{aligned} - \frac{2}{3} \cdot \frac{7}{9} = - \frac{2 \cdot 7}{3 \cdot 9} & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = - \frac{14}{27} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]
It is not required that you physically show the middle step. If you want to do that mentally, then you can simply write
\[ - \frac{2}{3} \cdot \frac{7}{9} = - \frac{14}{27}.\nonumber \]
Multiply:
\[ - \frac{3}{5} \cdot \frac{2}{7}\nonumber \]
- Answer
-
\[ - \frac{6}{35}\nonumber \]
Multiply and Reduce
After multiplying two fractions, make sure your answer is reduced to lowest terms (see Section 4.1).
Multiply 3/4 times 8/9.
Solution
After multiplying, divide numerator and denominator by the greatest common divisor of the numerator and denominator.
\[ \begin{aligned} \frac{3}{4} \cdot \frac{8}{9} = \frac{3 \cdot 8}{4 \cdot 9} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = \frac{24}{36} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = \frac{24 \div 12}{36 \div 12} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by GCD.}} \\ = \frac{2}{3} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Alternatively, after multiplying, you can prime factor both numerator and denominator, then cancel common factors.
\[ \begin{aligned} \frac{3}{4} \cdot \frac{8}{9} = \frac{24}{36} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = \frac{2 \cdot 2 \cdot 2 \cdot 3}{2 \cdot 2 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = = \frac{\cancel{2} \cdot \cancel{2} \cdot 2 \cdot \cancel{3}}{\cancel{2} \cdot \cancel{2} \cdot 3 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2}{3} ~ \end{aligned}\nonumber \]
Multiply:
\[ \frac{3}{7} \cdot \frac{14}{9}\nonumber \]
- Answer
-
\[ \frac{2}{3}\nonumber \]
Multiply −7x/2 and 5/(14x2).
Solution
After multiplying, prime factor both numerator and denominator, then cancel common factors. Note that unlike signs yields a negative product.
\[ \begin{aligned} - \frac{7x}{2} \cdot \frac{5}{14x^2} = - \frac{35x}{28x^2} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = - \frac{5 \cdot 7 \cdot x}{2 \cdot 2 \cdot 7 \cdot x \cdot x} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = - \frac{5 \cdot \cancel{7} \cdot \cancel{x}}{2 \cdot 2 \cdot \cancel{7} \cdot \cancel{x} \cdot x} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{5}{4x} \end{aligned}\nonumber \]
Multiply:
\[ - \frac{3x}{2} \cdot \frac{6}{21x^3}\nonumber \]
- Answer
-
\[ - \frac{3}{7x^2}\nonumber \]
Multiply and Cancel or Cancel and Multiply
When you are working with larger numbers, it becomes a bit harder to multiply, factor, and cancel. Consider the following argument.
\[ \begin{aligned} \frac{18}{30} \cdot \frac{35}{6} = \frac{630}{180} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{2 \cdot 3 \cdot 3 \cdot 5 \cdot 7}{2 \cdot 2 \cdot 3 \cdot 3 \cdot 5} ~ & \textcolor{red}{ \text{ Prime factor numerators and denominators.}} \\ = \frac{ \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{5} \cdot 7}{2 \cdot \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{5}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{7}{2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]
There are a number of difficulties with this approach. First, you have to multiply large numbers, and secondly, you have to prime factor the even larger results.
One possible workaround is to not bother multiplying numerators and denominators, leaving them in factored form.
\[ \begin{aligned} \frac{18}{30} \cdot \frac{35}{6} = \frac{18 \cdot 35}{30 \cdot 6} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{aligned}\nonumber \]
Finding the prime factorization of these smaller factors is easier.
\[ \begin{aligned} = \frac{(2 \cdot 3 \cdot 3) \cdot (5 \cdot 7)}{(2 \cdot 3 \cdot 5) \cdot (2 \cdot 3)} ~ & \textcolor{red}{ \text{ Prime factor.}} \end{aligned}\nonumber \]
Now we can cancel common factors. Parentheses are no longer needed in the numerator and denominator because both contain a product of prime factors, so order and grouping do not matter.
\[ \begin{aligned} = \frac{ \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{5} \cdot \cancel{7}}{ \cancel{2} \cdot \cancel{3} \cdot \cancel{5} \cdot 2 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{7}{2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]
Another approach is to factor numerators and denominators in place, cancel common factors, then multiply.
\[ \begin{aligned} \frac{18}{30} \cdot \frac{35}{6} = \frac{2 \cdot 3 \cdot 3}{2 \cdot 3 \cdot 5} \cdot \frac{5 \cdot 7}{2 \cdot 3} ~ & \textcolor{red}{ \text{ Factor numerators and denominators.}} \\ = \frac{ \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{3}}{ \cancel{2} \cdot \cancel{3} \cdot \cancel{5}} \cdot \frac{ \cancel{5} \cdot 7}{2 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{7}{2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]
Note that this yields exactly the same result, 7/2.
When multiplying fractions, cancel common factors according to the following rule: “Cancel a factor in a numerator for an identical factor in a denominator.”
Find the product of 14/15 and 30/140.
Solution
Multiply numerators and multiply denominators. Prime factor, cancel common factors, then multiply.
\[ \begin{aligned} \frac{14}{15} \cdot \frac{30}{140} = \frac{14 \cdot 30}{15 \cdot 140} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{(2 \cdot 7) \cdot (2 \cdot 3 \cdot 5)}{(3 \cdot 5) \cdot (2 \cdot 2 \cdot 5 \cdot 7)} ~ & \textcolor{red}{ \text{ Prime factor numerators and denominators.}} \\ = \frac{ \cancel{2} \cdot \cancel{7} \cdot \cancel{2} \cdot \cancel{3} \cdot \cancel{5}}{ \cancel{3} \cdot 5 cdot \cancel{2} \cdot \cancel{2} \cdot \cancel{5} \cdot \cancel{7}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{1}{5} ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]
Note: Everything in the numerator cancels because you’ve divided the numerator by itself. Hence, the answer has a 1 in its numerator.
Multiply:
\[ \frac{6}{35} \cdot \frac{70}{36}\nonumber \]
- Answer
-
\(\frac{1}{3}\)
When all the factors in the numerator cancel, this means that you are dividing the numerator by itself. Hence, you are left with a 1 in the numerator. The same rule applies to the denominator. If everything in the denominator cancels, you’re left with a 1 in the denominator.
Simplify the product: \( - \frac{6x}{55y} \cdot \left( - \frac{110y^2}{105x^2} \right).\nonumber \]
Solution
The product of two negatives is positive.
\[ \begin{aligned} - \frac{6x}{55y} \cdot \left( - \frac{110y^2}{105x^2} \right) = \frac{6x}{55y} \cdot \frac{110y^2}{105x^2} ~ & \textcolor{red}{ \text{ Like signs gives a positive.}} \end{aligned}\nonumber \]
Prime factor numerators and denominators, then cancel common factors.
\[ \begin{aligned} = \frac{2 \cdot 3 \cdot x}{5 \cdot 11 \cdot y} \cdot \frac{2 \cdot 5 \cdot 11 \cdot y \cdot y}{3 \cdot 5 \cdot 7 \cdot x \cdot x} ~ & \textcolor{red}{ \text{ Prime factor numerators & denominators.}} \\ = \frac{2 \cdot \cancel{3} \cdot \cancel{x}}{5 \cdot \cancel{11} \cdot \cancel{y}} \cdot \frac{2 \cdot \cancel{5} \cdot \cancel{11} \cdot \cancel{y} \cdot y}{ \cancel{3} \cdot \cancel{5} \cdot 7 \cdot \cancel{x} \cdot x} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2 \cdot 2 \cdot y}{5 \cdot 7 \cdot x} ~ & \textcolor{red}{ \text{ Remaining factors.}} \\ = \frac{4y}{35x} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{aligned}\nonumber \]
Simplify:
\[ \frac{6x}{15b} \cdot \left( - \frac{35b^2}{10a^2} \right)\nonumber \]
- Answer
-
\[ - \frac{21b}{5a}\nonumber \]
Parallelograms
In this section, we are going to learn how to find the area of a parallelogram. Let’s begin with the definition of a parallelogram. Recall that a quadrilateral is a polygon having four sides. A parallelogram is a very special type of quadrilateral.
A parallelogram is a quadrilateral whose opposite sides are parallel.
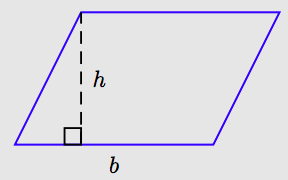
The side on which the parallelogram rests is called its base (labeled b in the figure) and the distance from its base to the opposite side is called its height (labeled h in the figure). Note that the altitude is perpendicular to the base (meets the base at a 90◦ angle).
Figure 4.8 shows a rectangle having length b and width h. Therefore, the area of the rectangle in Figure 4.8 is A = bh, which is found by taking the product of the length and width. Take a pair of scissors and cut a triangle from the right end of the rectangle as shown in Figure 4.9(a), then paste the cut triangle to the left end as shown in Figure 4.9(b). The result, seen in Figure 4.9(b) is a parallelogram having base b and height h.
Because we’ve thrown no material away in creating the parallelogram from the rectangle, the parallelogram has the same area as the original rectangle. That is, the area of the parallelogram is A = bh.
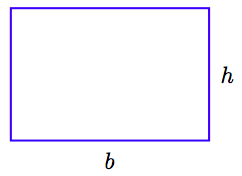
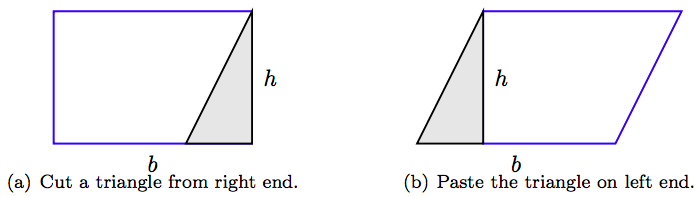
A parallelogram having base b and height h has area A = bh. That is, to find the area of a parallelogram, take the product of its base and height.
Find the area of the parallelogram pictured below.
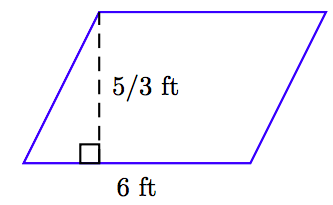
Solution
The area of the parallelogram is equal to the product of its base and height. That is,
\[ \begin{aligned} A = bh ~ & \textcolor{red}{ \text{ Area formula for a parallelogram.}} \\ = (6 \text{ ft}) \left( \frac{5}{3} \text{ ft} \right) ~ & \textcolor{red}{ \text{ Substitute: 6 ft for }b, \text{ 5/3 ft for } h.} \\ = \frac{30}{3} \text{ ft}^2. ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = 10 \text{ ft}^2. ~ & \textcolor{red}{ \text{ Divide.}} \end{aligned}\nonumber \]
Thus, the area of the parallelogram is 10 square feet.
The base of a parallelogram measures 14 inches. The height is 8/7 of an inch. What is the area of the parallelogram?
- Answer
-
16 square inches
Triangles
Let’s turn our attention to learning how to find the area of a triangle.
A triangle is a three-sided polygon. It is formed by plotting three points and connecting them with three line segments. Each of the three points is called a vertex of the triangle and each of the three line segments is called a side of the triangle.
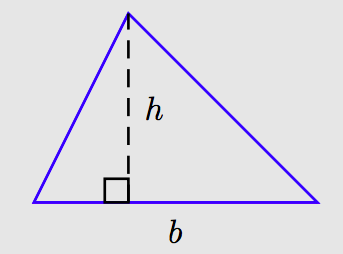
The side on which the triangle rests is called its base, and the distance between its base and opposite vertex is called its height of altitude. The altitude is always perpendicular to the base; that is, it forms a 90◦ angle with the base.
It’s easily seen that a triangle has half the area of a parallelogram.
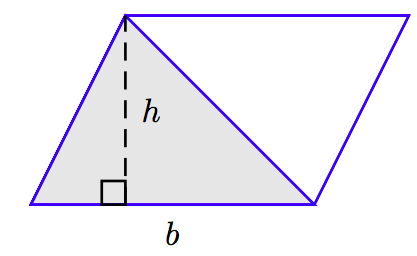
The parallelogram has area A = bh. Therefore, the triangle has one-half that area. That is, the area of the triangle is A = (1/2)bh.
A triangle having base b and height h has area A = (1/2)bh. That is, to find the area of a triangle, take one-half the product of the base and height.
Find the area of the triangle pictured below.
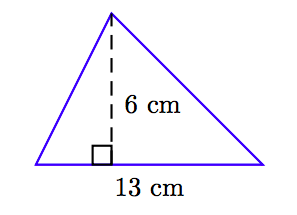
Solution
To find the area of the triangle, take one-half the product of the base and height.
\[ \begin{aligned} A = \frac{1}{2} bh ~ & \textcolor{red}{ \text{ Area of a triangle formula.}} \\ = \frac{1}{2} (13 \text{ cm}) (6 \text{ cm}) ~ & \textcolor{red}{ \text{ Substitute: 13 cm for } b,~ \text{6 cm for } h.} \\ = \frac{78 \text{ cm}^2}{2} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = 39 \text{ cm}^2. ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Therefore, the area of the triangle is 39 square centimeters.
The base of a triangle measures 15 meters. The height is 12 meters. What is the area of the triangle?
- Answer
-
90 square meters
Identifying the Base and Altitude
Sometimes it can be a bit difficult to determine the base and altitude (height) of a triangle. For example, consider the triangle in Figure 4.10(a). Let’s say we choose the bottom edge of the triangle as the base and denote its length with the variable b, as shown in Figure 4.10(a).
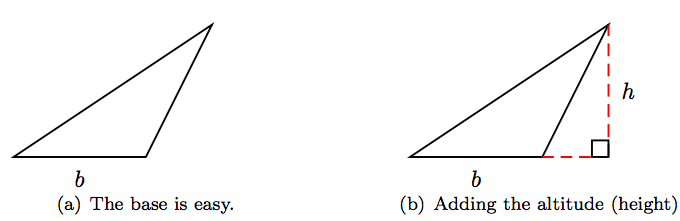
The altitude (height) of the triangle is defined as the distance between the base of the triangle and its opposite vertex. To identify this altitude, we must first extend the base, as seen in the dashed extension in Figure 4.10(b), then drop a perpendicular dashed line from the opposite vertex to the extended base, also shown in Figure 4.10(b). This perpendicular is the altitude (height) of the triangle and we denote its length by h.
But we can go further. Any of the three sides of a triangle may be designated as the base of the triangle. Suppose, as shown in Figure 4.11(a), we identify a different side as the base, with length denoted by the variable b.
The altitude to this new base will be a segment from the opposite vertex, perpendicular to the base. Its length in Figure 4.11(b) is denoted by h.
In like manner, there is a third side of the triangle that could also be used as the base. The altitude to this third side is found by dropping a perpendicular from the vertex of the triangle directly opposite from this base. This would also require extending the base. We leave this to our readers to explore.
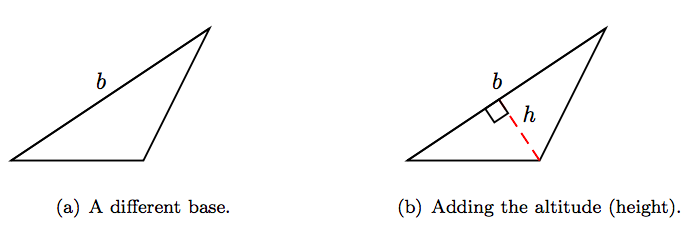
Any of the three sides of a triangle may be used as the base. The altitude is drawn by dropping a perpendicular from the opposite vertex to the chosen base. This sometimes requires that we extend the base. Regardless of which side we use for the base, the formula A = bh/2 will produce the same area result.
Exercises
1. Create a diagram, such as that shown in Figure 4.7, to show that 1/3 of 1/3 is 1/9.
2. Create a diagram, such as that shown in Figure 4.7, to show that 1/2 of 1/4 is 1/8.
3. Create a diagram, such as that shown in Figure 4.7, to show that 1/3 of 1/4 is 1/12.
4. Create a diagram, such as that shown in Figure 4.7, to show that 2/3 of 1/3 is 2/9.
In Exercises 1-28, multiply the fractions, and simplify your result.
5. \(\frac{−21}{4} \cdot \frac{22}{19}\)
6. \(\frac{−4}{19} \cdot \frac{21}{8}\)
7. \(\frac{20}{11} \cdot \frac{−17}{22}\)
8. \(\frac{−9}{2} \cdot \frac{6}{7}\)
9. \(\frac{21}{8} \cdot \frac{−14}{15}\)
10. \(\frac{−17}{18} \cdot \frac{−3}{4}\)
11. \(\frac{−5}{11} \cdot \frac{7}{20}\)
12. \(\frac{−5}{2} \cdot \frac{−20}{19}\)
13. \(\frac{8}{13} \cdot \frac{−1}{6}\)
14. \(\frac{−12}{7} \cdot \frac{5}{9}\)
15. \(\frac{2}{15} \cdot \frac{−9}{8}\)
16. \(\frac{2}{11} \cdot \frac{−21}{8}\)
17. \(\frac{17}{12} \cdot \frac{3}{4}\)
18. \(\frac{7}{13} \cdot \frac{10}{21}\)
19. \(\frac{−6}{23} \cdot \frac{9}{10}\)
20. \(\frac{12}{11} \cdot \frac{−5}{2}\)
21. \(\frac{−23}{24} \cdot \frac{−6}{17}\)
22. \(\frac{4}{9} \cdot \frac{−21}{19}\)
23. \(\frac{24}{7} \cdot \frac{5}{2}\)
24. \(\frac{−20}{23} \cdot \frac{−1}{2}\)
25. \(\frac{1}{2} \cdot \frac{−8}{11}\)
26. \(\frac{−11}{18} \cdot \frac{−20}{3}\)
27. \(\frac{−24}{13} \cdot \frac{−7}{18}\)
28. \(\frac{21}{20} \cdot \frac{−4}{5}\)
In Exercises 29-40, multiply the fractions, and simplify your result.
29. \(\frac{−12y^3}{13} \cdot \frac{2}{9y^6}\)
30. \(\frac{−8x^3}{3} \cdot \frac{−6}{5x^5}\)
31. \(\frac{11y^3}{24} \cdot \frac{6}{5y^5}\)
32. \(\frac{11y}{18} \cdot \frac{21}{17y^6}\)
33. \(\frac{−8x^2}{21} \cdot \frac{−18}{19x}\)
34. \(\frac{2y^4}{11} \cdot \frac{−7}{18y}\)
35. \(\frac{13x^6}{15} \cdot \frac{9}{16x^2}\)
36. \(\frac{−22x^6}{15} \cdot \frac{17}{16x^3}\)
37. \(\frac{−6y^3}{5} \cdot \frac{−20}{7y^6}\)
38. \(\frac{−21y}{5} \cdot \frac{−8}{3y^2}\)
39. \(\frac{−3y^3}{4} \cdot \frac{23}{12y}\)
40. \(\frac{−16y^6}{15} \cdot \frac{−21}{13y^4}\)
In Exercises 41-56, multiply the fractions, and simplify your result.
41. \(\frac{13y^6}{20x^4} \cdot \frac{2x}{7y^2}\)
42. \(\frac{−8y^3}{13x^6} \cdot \frac{7x^2}{10y^2}\)
43. \(\frac{23y^4}{21x} \cdot \frac{−7x^6}{4y^2}\)
44. \(\frac{−2x^6}{9y^4} \cdot \frac{y^5}{20x}\)
45. \(\frac{11y^6}{12x^6} \cdot \frac{−2x^4}{7y^2}\)
46. \(\frac{16x^3}{13y^4} \cdot \frac{11y^2}{18x}\)
47. \(\frac{x^6}{21y^3} \cdot \frac{−7y^4}{9x^5}\)
48. \(\frac{−3y^3}{5x} \cdot \frac{14x^5}{15y^2}\)
49. \(\frac{19y^2}{18x} \cdot \frac{10x^3}{7y^3}\)
50. \(\frac{−20x}{9y^3} \cdot \frac{−y^6}{4x^3}\)
51. \(\frac{−4y^3}{5x^5} \cdot \frac{−10x}{21y^4}\)
52. \(\frac{11y^2}{14x^4} \cdot \frac{−22x}{21y^3}\)
53. \(\frac{−16x}{21y^2} \cdot \frac{−7y^3}{5x^2}\)
54. \(\frac{−4y}{5x} \cdot \frac{10x^3}{7y^6}\)
55. \(\frac{17x^3}{3y^6} \cdot \frac{−12y^2}{7x^4}\)
56. \(\frac{−6x^4}{11y^3} \cdot \frac{13y^2}{8x^5}\)
In Exercises 57-62, find the area of the parallelogram having the given base and altitude.
57. base = 8 cm, altitude = 7 cm
58. base = 2 cm, altitude = 11 cm
59. base = 6 cm, altitude = 13 cm
60. base = 2 cm, altitude = 6 cm
61. base = 18 cm, altitude = 14 cm
62. base = 20 cm, altitude = 2 cm
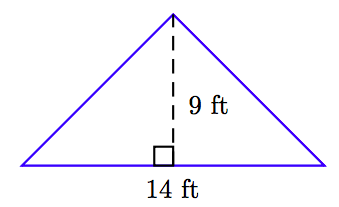
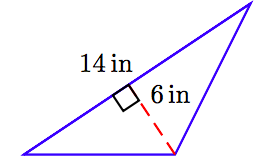
In Exercises 63-68, find the area of the triangle shown in the figure. (Note: Figures are not drawn to scale.)
63.
64.
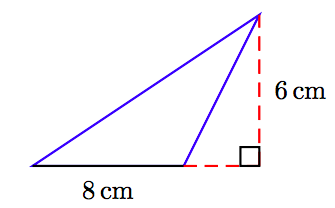
65.
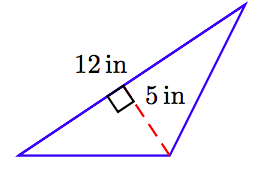
66.
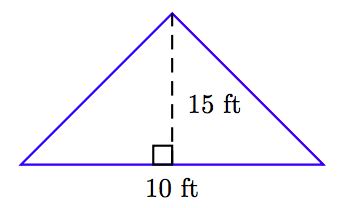
67.
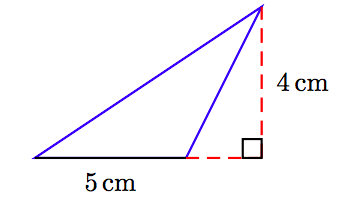
68.
69. Weight on the Moon. On the moon, you would only weigh 1/6 of what you weigh on earth. If you weigh 138 pounds on earth, what would your weight on the moon be?
Answers
1. This shows that 1/3 of 1/3 is 1/9.

3. This shows that 1/3 of 1/4 is 1/12.
5. \(\frac{−231}{38}\)
7. \(\frac{−170}{121}\)
9. \(\frac{−49}{20}\)
11. \(\frac{−7}{44}\)
13. \(\frac{−4}{39}\)
15. \(\frac{−3}{20}\)
17. \(\frac{17}{16}\)
19. \(\frac{−27}{115}\)
21. \(\frac{23}{68}\)
23. \(\frac{60}{7}\)
25. \(\frac{−4}{11}\)
27. \(\frac{28}{39}\)
29. \(− \frac{8}{39y^3}\)
31. \(\frac{11}{20y^2}\)
33. \(\frac{48x}{133}\)
35. \(\frac{39x^4}{80}\)
37. \(\frac{24}{7y^3}\)
39. \(− \frac{23y^2}{16}\)
41. \(\frac{13y^4}{70x^3}\)
43. \(− \frac{23y^2x^5}{12}\)
45. \(− \frac{11y^4}{42x^2}\)
47. \(− \frac{xy}{27}\)
49. \(\frac{95x^2}{63y}\)
51. \(\frac{8}{21yx^4}\)
53. \(\frac{16y}{15x}\)
55. \(− \frac{68}{7xy^4}\)
57. 56 cm2
59. 78 cm2
61. 252 cm2
63. 63 ft2
65. 30 in2
67. 10 cm2
69. 23 pounds


