4.2: Equivalent Fractions
- Page ID
- 22480
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we deal with fractions, numbers or expressions of the form a/b.
A number of the form
\[ \dfrac{a}{b}\nonumber \]
where \(a\) and \(b\) are numbers is called a fraction. The number \(a\) is called the numerator of the fraction, while the number \(b\) is called the denominator of the fraction.
Near the end of this section, we’ll see that the numerator and denominator of a fraction can also be algebraic expressions, but for the moment we restrict our attention to fractions whose numerators and denominators are integers. We start our study of fractions with the definition of equivalent fractions.
Two fractions are equivalent if they represent the same numerical value.
But how can we tell if two fractions represent the same number? Well, one technique involves some simple visualizations. Consider the image shown in Figure 4.1, where the shaded region represents 1/3 of the total area of the figure (one of three equal regions is shaded).

In Figure 4.2, we’ve shaded 2/6 of the entire region (two of six equal regions are shaded).

In Figure 4.3, we’ve shaded 4/12 of the entire region (four of twelve equal regions are shaded).
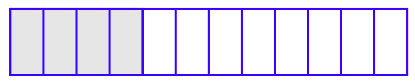
Let’s take the diagrams from Figure 4.1, Figure 4.2, and Figure 4.3 and stack them one atop the other, as shown in Figure 4.4.
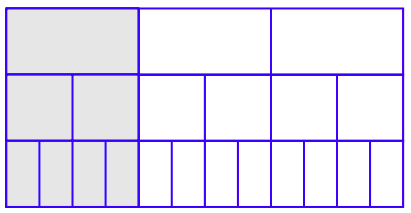
Figure 4.4 provides solid visual evidence that the following fractions are equivalent.
\[ \dfrac{1}{3} = \dfrac{2}{6} = \dfrac{4}{12}\nonumber \]
Key Observations
1. If we start with the fraction 1/3, then multiply both numerator and denominator by 2, we get the following result.
\[ \begin{aligned} \dfrac{1}{3} = \dfrac{1 \cdot 2}{3 \cdot 2} ~ & \textcolor{red}{ \text{ Multiply the numerator and denominator by 2.}} \\ = \dfrac{2}{6} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
This is precisely the same thing that happens going from Figure 4.1 to 4.2, where we double the number of available boxes (going from 3 available to 6 available) and double the number of shaded boxes (going from 1 shaded to 2 shaded).
2. If we start with the fraction 1/3, then multiply both numerator and denominator by 4, we get the following result.
\[ \begin{aligned} = \dfrac{1}{3} = \dfrac{1 \cdot 4}{3 \cdot 4} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 4.}} \\ = \dfrac{4}{12} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
This is precisely the same thing that happens going from Figure 4.1 to 4.3, where we multiply the number of available boxes by 4 (going from 3 available to 12 available) and multiply the number of shaded boxes by 4 (going from 1 shaded to 4 shaded).
The above discussion motivates the following fundamental result.
If you start with a fraction, then multiply both its numerator and denominator by the same number, the resulting fraction is equivalent (has the same numerical value) to the original fraction. In symbols,
\[ \dfrac{a}{b} = \dfrac{a \cdot x}{b \cdot x}\nonumber \]
Arguing in Reverse
Reversing the above argument also holds true.
1. If we start with the fraction 2/6, then divide both numerator and denominator by 2, we get the following result.
\[ \begin{aligned} \dfrac{2}{6} = \dfrac{2 \div 2}{6 \div 2} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 2.}} \\ = \dfrac{1}{3} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
This is precisely the same thing that happens going backwards from Figure 4.2 to 4.1, where we divide the number of available boxes by 2 (going from 6 available to 3 available) and dividing the number of shaded boxes by 2 (going from 2 shaded to 1 shaded).
2. If we start with the fraction 4/12, then divide both numerator and denominator by 4, we get the following result.
\[ \begin{aligned} \dfrac{4}{12} = \dfrac{4 \div 4}{12 \div 4} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 4.}} \\ = \dfrac{1}{3} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
This is precisely the same thing that happens going backwards from Figure 4.3 to 4.1, where we divide the number of available boxes by 4 (going from 12 available to 3 available) and divide the number alignof shaded boxes by 4 (going from 4 shaded to 1 shaded).
The above discussion motivates the following fundamental result.
If you start with a fraction, then divide both its numerator and denominator by the same number, the resulting fraction is equivalent (has the same numerical value) to the original fraction. In symbols,
\[ \dfrac{a}{b} = \dfrac{a \div x}{b \div x}.\nonumber \]
The Greatest Common Divisor
We need a little more terminology.
If d and a are natural numbers, we say that “d divides a” if and only if when a is divided by d, the remainder is zero. In this case, we say that “d is a divisor of a.”
For example, when 36 is divided by 4, the remainder is zero. In this case, we say that “4 is a divisor of 36.” On the other hand, when 25 is divided by 4, the remainder is not zero. In this case, we say that “4 is not a divisor of 25.”
Let a and b be natural numbers. The common divisors of a and b are those natural numbers that divide both a and b. The greatest common divisor is the largest of these common divisors.
Find the greatest common divisor of 18 and 24.
Solution
First list the divisors of each number, the numbers that divide each number with zero remainder.
Divisors of 18 : 1, 2, 3, 6, 9, and 18
Divisors of 24 : 1, 2, 3, 4, 6, 8, 12, and 24
The common divisors are:
Common Divisors : 1, 2, 3, and 6
The greatest common divisor is the largest of the common divisors. That is,
Greatest Common Divisor = 6.
That is, the largest number that divides both 18 and 24 is the number 6.
Find the greatest common divisor of 12 and 18.
- Answer
-
6
Reducing a Fraction to Lowest Terms
First, a definition.
A fraction is said to be reduced to lowest terms if the greatest common divisor of both numerator and denominator is 1.
Thus, for example, 2/3 is reduced to lowest terms because the greatest common divisior of 2 and 3 is 1. On the other hand, 4/6 is not reduced to lowest terms because the greatest common divisor of 4 and 6 is 2.
Reduce the fraction 18/24 to lowest terms.
Solution
One technique that works well is dividing both numerator and denominator by the greatest common divisor of the numerator and denominator. In Example 1, we saw that the greatest common divisor of 18 and 24 is 6. We divide both numerator and denominator by 6 to get
\[ \begin{aligned} \dfrac{18}{24} = \dfrac{18 \div 6}{24 \div 6} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 6.}} \\ = \dfrac{3}{4} ~ & \textcolor{red}{ \text{ Simplify numerator and dice.}} \end{aligned}\nonumber \]
Note that the greatest common divisor of 3 and 4 is now 1. Thus, 3/4 is reduced to lowest terms.
There is a second way we can show division of numerator and denominator by 6. First, factor both numerator and denominator as follows:
\[ \begin{aligned} \dfrac{18}{24} = \dfrac{3 \cdot 6}{4 \cdot 6} ~ & \textcolor{red}{ \text{ Factor out a 6.}} \end{aligned}\nonumber \]
You can then show “division” of both numerator and denominator by 6 by “crossing out” or “canceling” a 6 in the numerator for a 6 in the denominator, like this:
\[ \begin{aligned} = \dfrac{3 \cdot \cancel{6}}{4 \cdot \cancel{6}} ~ & \textcolor{red}{ \text{ Cancel common factor.}} \\ = \dfrac{3}{4} \end{aligned}\nonumber \]
Note that we get the same equivalent fraction, reduced to lowest terms, namely 3/4.
Reduce the fraction 12/18 to lowest terms.
- Answer
-
2/3
In Example 2 we saw that 6 was both a divisor and a factor of 18. The words divisor and factor are equivalent.
We used the following technique in our second solution in Example 2.
If you express numerator and denominator as a product, then you may cancel common factors from the numerator and denominator. The result will be an equivalent fraction.
Because of the “Cancellation Rule,” one of the most effective ways to reduce a fraction to lowest terms is to first find prime factorizations for both numerator and denominator, then cancel all common factors.
Reduce the fraction 18/24 to lowest terms.
Solution
Use factor trees to prime factor numerator and denominator.
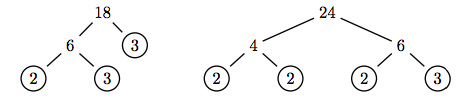
Once we’ve factored the numerator and denominator, we cancel common factors.
\[ \begin{aligned} \dfrac{18}{24} = \dfrac{2 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \dfrac{ \cancel{2} \cdot \cancel{3} \cdot 3}{ \cancel{2} \cdot 2 \cdot 2 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \dfrac{3}{2 \cdot 2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \\ = \dfrac{3}{4} ~ & \textcolor{red}{ \text{ Simplify denominator.}} \end{aligned}\nonumber \]
Thus, 18/24 = 3/4.
Reduce the fraction 28/35 to lowest terms.
- Answer
-
4/5
Reduce the fraction 28/42 to lowest terms.
Solution
Use factor trees to prime factor numerator and denominator.
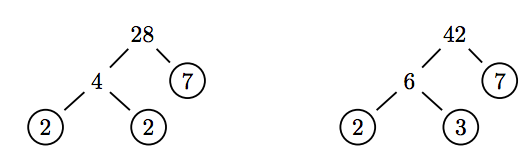
Now we can cancel common factors.
\[ \begin{aligned} \dfrac{28}{42} = \dfrac{2 \cdot 2 \cdot 7}{2 \cdot 3 \cdot 7} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \dfrac{ \cancel{2} \cdot 2 \cdot \cancel{7}}{ \cancel{2} \cdot 3 \cdot \cancel{7}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \dfrac{2}{3} \end{aligned}\nonumber \]
Thus, 28/42 = 2/3.
Reduce the fraction 36/60 to lowest terms.
- Answer
-
3/5
Reducing Fractions with Variables
We use exactly the same technique to reduce fractions whose numerators and denominators contain variables.
Reduce
\[ \dfrac{56x^2y}{60xy^2}\nonumber \]
to lowest terms.
Solution
Use factor trees to factor the coefficients of numerator and denominator.

Now cancel common factors.
\[ \begin{aligned} \dfrac{56x^2y}{60xy^2} = \dfrac{2 \cdot 2 \cdot 2 \cdot 7 \cdot x \cdot x \cdot y}{2 \cdot 2 \cdot 3 \cdot 5 \cdot x \cdot y \cdot y} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \dfrac{ \cancel{2} \cdot \cancel{2} \cdot 2 \cdot 7 \cdot \cancel{x} \cdot x \cdot \cancel{y}}{ \cancel{2} \cdot \cancel{2} \cdot 3 \cdot 5 \cdot \cancel{x} \cdot y \cdot \cancel{y}} ~ & \textcolor{red}{ \text{ Cancel cmmon factors.}} \\ = \dfrac{2 \cdot 7 \cdot x}{3 \cdot 5 \cdot y} ~ & \textcolor{red}{ \text{ Remaining factors.}} \\ = \dfrac{14x}{15y} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Thus, 56x2y/(60xy2) = 14x/(15y).
Reduce:
\[ \dfrac{25a^3b}{40a^2b^3}\nonumber \]
- Answer
-
\[ \dfrac{5a}{8b^2}\nonumber \]
A Word on Mathematical Notation
There are two types of mathematical notation: (1) inline mathematical notation, and (2) displayed mathematical notation.
The notation 14x/(15y) is called inline mathematical notation. When the same expression is centered on its own line, as in
\[ \dfrac{14x}{15y},\nonumber \]
this type of notation is called displayed mathematical notation.
When you work a problem by hand, using pencil and paper calculations, the preferred format is displayed notation, like the displayed notation used to simplify the given expression in Example 5. However, computers and calculators require that you enter your expressions using inline mathematical notation. Therefore, it is extremely important that you are equally competent with either mathematical notation: displayed or inline.
By the way, order of operations, when applied to the inline expression 14x/(15y), requires that we perform the multiplication inside the parentheses first. Then we must perform multiplications and divisions as they occur, as we move from left to right through the expression. This is why the inline notation 14x/(15y) is equivalent to the displayed notation
\[ \dfrac{14x}{15y}.\nonumber \]
However, the expression 14x/15y is a different beast. There are no parentheses, so we perform multiplication and division as they occur, moving left to right through the expression. Thus, we must first take the product of 14 and x, divide the result by 15, then multiply by y. In displayed notation, this result is equivalent to
\[ \dfrac{14x}{15} \cdot y,\nonumber \]
which is a different result.
Some readers might wonder why we did not use the notation (14x)/(15y) to describe the solution in Example 5. After all, this inline notation is also equivalent to the displayed notation
\[ \dfrac{14x}{15y}.\nonumber \]
However, the point is that we do not need to, as order of operations already requires that we take the product of 14 and x before dividing by 15y. If this is hurting your head, know that it’s quite acceptable to use the equivalent notation (14x)/(15y) instead of 14x/(15y). Both are correct.
Equivalent Fractions in Higher Terms
Sometimes the need arises to find an equivalent fraction with a different, larger denominator.
Express 3/5 as an equivalent fraction having denominator 20.
Solution
The key here is to remember that multiplying numerator and denominator by the same number produces an equivalent fraction. To get an equivalent fraction with a denominator of 20, we’ll have to multiply numerator and denominator of 3/5 by 4.
\[ \begin{aligned} \dfrac{3}{5} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 4.}} \\ = \dfrac{12}{20} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Therefore, 3/5 equals 12/20.
Express 2/3 as an equivalent fraction having denominator 21.
- Answer
-
14/21
Express 8 as an equivalent fraction having denominator 5.
Solution
The key here is to note that
\[ \begin{aligned} 8 = \dfrac{8}{1} ~ & \textcolor{red}{ \text{ Understood denominator is 1.}} \end{aligned}\nonumber \]
To get an equivalent fraction with a denominator of 5, we’ll have to multiply numerator and denominator of 8/1 by 5.
\[ \begin{aligned} = \dfrac{8 \cdot 5}{1 \cdot 5} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 5.}} \\ = \dfrac{40}{5} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Therefore, 8 equals 40/5.
Express 5 as an equivalent fraction having denominator 7.
- Answer
-
35/7
Express 2/9 as an equivalent fraction having denominator 18a.
Solution
To get an equivalent fraction with a denominator of 18a, we’ll have to multiply numerator and denominator of 2/9 by 2a.
\[ \begin{aligned} \dfrac{2}{9} = \dfrac{2 \cdot 2a}{9 \cdot 2a} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by } 2a.} \\ = \dfrac{4a}{18a} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Therefore, 2/9 equals 4a/(18a), or equivalently, (4a)/(18a).
Express 3/8 as an equivalent fraction having denominator 24a.
- Answer
-
\[ \dfrac{9a}{24a}\nonumber \]
Negative Fractions
We have to also deal with fractions that are negative. First, let’s discuss placement of the negative sign.
- Positive divided by negative is negative, so
\[ \dfrac{3}{-5} = - \dfrac{3}{5}.\nonumber \]
- But it is also true that negative divided by positive is negative. Thus,
\[ \dfrac{−3}{5} = \dfrac{−3}{5}.\nonumber \]
These two observations imply that all three of the following fractions are equivalent (the same number):
\[ \dfrac{3}{-5} = - \dfrac{3}{5} = \dfrac{-3}{5}.\nonumber \]
Note that there are three possible placements for the negative sign: (1) the denominator, (2) the fraction bar, or (3) the numerator. Any one of these placements produces an equivalent fraction.
Let a and b be any integers. All three of the following fractions are equivalent (same number):
\[ \dfrac{a}{-b} = - \dfrac{a}{b} = \dfrac{-a}{b}.\nonumber \]
Mathematicians prefer to place the negative sign either in the numerator or on the fraction bar. The use of a negative sign in the denominator is discouraged.
Reduce:
\[ \dfrac{50x^3}{-75x^5}\nonumber \]
to lowest terms.
Solution
Prime factor numerator and denominator and cancel.
\[ \begin{aligned} \dfrac{50x^3}{-75x^5} &= \dfrac{2 \cdot 5 \cdot 5 \cdot x \cdot x \cdot x}{-3 \cdot 5 \cdot 5 \cdot x \cdot x \cdot x \cdot x \cdot x} \\ &= \dfrac{2 \cdot \cancel{5} \cdot \cancel{5} \cdot \cancel{x} \cdot \cancel{x} \cdot \cancel{x}}{-3 \cdot \cancel{5} \cdot \cancel{5} \cdot \cancel{x} \cdot \cancel{x} \cdot \cancel{x} \cdot x \cdot x} \\ &= \dfrac{2}{-3 \cdot x \cdot x} \\ &= \dfrac{2}{-3x^2} \end{aligned}\nonumber \]
However, it is preferred that there be no negative signs in the denominator, so let’s place the negative sign on the fraction bar (the numerator would suit as well). Thus,
\[ \dfrac{50x^3}{-75x^5} = - \dfrac{2}{3x^2}\nonumber \]
We also have the following result.
Let \(a\) and \(b\) be any integers. Then,
\[ \dfrac{-a}{-b} = \dfrac{a}{b}.\nonumber \]
Reduce:
\[ \dfrac{-12xy^2}{-18x^2y}\nonumber \]
Solution
Unlike Example 9, some like to take care of the sign of the answer first.
\[ \dfrac{-12xy^2}{-18x^2y} = \dfrac{12xy^2}{18x^2y}\nonumber \]
Now we can factor numerator and denominator and cancel common factors.
\[ \begin{aligned} &= \dfrac{2 \cdot 2 \cdot 3 \cdot x \cdot y \cdot y}{2 \cdot 3 \cdot 3 \cdot x \cdot x \cdot y} \\ &= \dfrac{ \cancel{2} \cdot 2 \cancel{3} \cdot \cancel{x} \cdot y \cdot \cancel{y}}{ \cancel{2} \cdot \cancel{3} \cdot 3 \cdot \cancel{x} \cdot x \cdot \cancel{y}} &= \dfrac{2y}{3x} \end{aligned}\nonumber \]
Thus,
\[ \dfrac{-12xy^2}{-18x^2y} = \dfrac{2y}{3x}.\nonumber \]
Reduce:
\[ \dfrac{-21a^2b^3}{-56a^3b}\nonumber \]
- Answer
-
\[ \dfrac{3b^2}{8a}\nonumber \]
Exercises
In Exercises 1-12, find the GCD of the given numbers.
1. 72, 8
2. 76, 52
3. 52, 20
4. 56, 96
5. 36, 63
6. 63, 21
7. 72, 44
8. 10, 40
9. 16, 56
10. 54, 66
11. 84, 24
12. 75, 45
In Exercises 13-28, reduce the given fraction to lowest terms.
13. \(\dfrac{22}{98}\)
14. \(\dfrac{28}{56}\)
15. \(\dfrac{93}{15}\)
16. \(\dfrac{90}{39}\)
17. \(\dfrac{69}{21}\)
18. \(\dfrac{74}{62}\)
19. \(\dfrac{74}{12}\)
20. \(\dfrac{66}{10}\)
21. \(\dfrac{66}{57}\)
22. \(\dfrac{34}{30}\)
23. \(\dfrac{33}{99}\)
24. \(\dfrac{20}{58}\)
25. \(\dfrac{69}{24}\)
26. \(\dfrac{18}{96}\)
27. \(\dfrac{46}{44}\)
28. \(\dfrac{92}{24}\)
29. Express 3 as an equivalent fraction having denominator 24. 30. Express 3 as an equivalent fraction having denominator 8. 31. Express \(\dfrac{25}{19}\) as an equivalent fraction having denominator 57. 32. Express \(\dfrac{29}{22}\) as an equivalent fraction having denominator 44. 33. Express 2 as an equivalent fraction having denominator 2. 34. Express 2 as an equivalent fraction having denominator 8. 35. Express \(\dfrac{18}{19}\) as an equivalent fraction having denominator 95. 36. Express \(\dfrac{17}{22}\) as an equivalent fraction having denominator 44. 37. Express \(\dfrac{1}{3}\) as an equivalent fraction having denominator 24. 38. Express \(\dfrac{15}{19}\) as an equivalent fraction having denominator 95. 39. Express 16 as an equivalent fraction having denominator 4. 40. Express 5 as an equivalent fraction having denominator 2.
In Exercises 41-56, reduce the given fraction to lowest terms.
41. \(\dfrac{34}{−86}\)
42. \(\dfrac{−48}{14}\)
43. \(\dfrac{−72}{−92}\)
44. \(\dfrac{27}{−75}\)
45. \(\dfrac{−92}{82}\)
46. \(\dfrac{−44}{−62}\)
47. \(\dfrac{−21}{33}\)
48. \(\dfrac{57}{−99}\)
49. \(\dfrac{22}{−98}\)
50. \(\dfrac{−33}{69}\)
51. \(\dfrac{42}{−88}\)
52. \(\dfrac{−100}{48}\)
53. \(\dfrac{94}{−6}\)
54. \(\dfrac{−36}{−38}\)
55. \(\dfrac{10}{−86}\)
56. \(\dfrac{−100}{−46}\)
57. Express \(\dfrac{3}{2}\) as an equivalent fraction having denominator 62n.
58. Express \(\dfrac{6}{25}\) as an equivalent fraction having denominator 50a.
59. Express \(\dfrac{13}{10}\) as an equivalent fraction having denominator 60m.
60. Express \(\dfrac{1}{16}\) as an equivalent fraction having denominator 80p.
61. Express \(\dfrac{3}{2}\) as an equivalent fraction having denominator 50n.
62. Express \(\dfrac{43}{38}\) as an equivalent fraction having denominator 76a.
63. Express 11 as an equivalent fraction having denominator 4m. 64. Express 13 as an equivalent fraction having denominator 6n.
65. Express 3 as an equivalent fraction having denominator 10m.
66. Express 10 as an equivalent fraction having denominator 8b.
67. Express 6 as an equivalent fraction having denominator 5n.
68. Express 16 as an equivalent fraction having denominator 2y.
In Exercises 69-84, reduce the given fraction to lowest terms.
69. \(\dfrac{82y^5}{−48y}\)
70. \(\dfrac{−40y^5}{−55y}\)
71. \(\dfrac{−77x^5}{44x^4}\)
72. \(\dfrac{−34x^6}{−80x}\)
73. \(\dfrac{−14y^5}{54y^2}\)
74. \(\dfrac{96y^4}{−40y^2}\)
75. \(\dfrac{42x}{81x^3}\)
76. \(\dfrac{26x^2}{32x^6}\)
77. \(\dfrac{−12x^5}{14x^6}\)
78. \(\dfrac{−28y^4}{72y^6}\)
79. \(\dfrac{−74x}{22x^2}\)
80. \(\dfrac{56x^2}{26x^3}\)
81. \(\dfrac{−12y^5}{98y^6}\)
82. \(\dfrac{96x^2}{14x^4}\)
83. \(\dfrac{18x^6}{−54x^2}\)
84. \(\dfrac{32x^6}{62x^2}\)
In Exercises 85-100, reduce the given fraction to lowest terms.
85. \(\dfrac{26y^2x^4}{−62y^6x^2}\)
86. \(\dfrac{6x^2y^3}{40x^3y^2}\)
87. \(\dfrac{−2y^6x^4}{−94y^2x^5}\)
88. \(\dfrac{90y^6x^3}{39y^3x^5}\)
89. \(\dfrac{30y^5x^5}{−26yx^4}\)
90. \( \dfrac{74x^6y^4}{−52xy^3}\)
91. \(\dfrac{36x^3y^2}{−98x^4y^5}\)
92. \(\dfrac{84x^3y}{16x^4y^2}\)
93. \(\dfrac{−8x^6y^3}{54x^3y^5}\)
94. \( \dfrac{70y^5x^2}{16y^4x^5}\)
95. \(\dfrac{34yx^6}{−58y^5x^4}\)
96. \(\dfrac{99y^2x^3}{88y^6x}\)
97. \(\dfrac{−36y^3x^5}{51y^2x}\)
98. \(\dfrac{44y^5x^5}{−88y^4x}\)
99. \(\dfrac{91y^3x^2}{−28y^5x^5}\)
100. \(\dfrac{−76y^2x}{−57y^5x^6}\)
101. Hurricanes. According to the National Atmospheric and Oceanic Administration, in 2008 there were 16 named storms, of which 8 grew into hurricanes and 5 were major.
i) What fraction of named storms grew into hurricanes? Reduce your answer to lowest terms.
ii) What fraction of named storms were major hurricanes? Reduce your answer to lowest terms.
iii) What fraction of hurricanes were major? Reduce your answer to lowest terms.
102. Tigers. Tigers are in critical decline because of human encroachment, the loss of more than nine-tenths of their habitat, and the growing trade in tiger skins and body parts. Associated Press-Times-Standard 01/24/10 Pressure mounts to save the tiger.
i) Write the loss of habitat as a fraction.
ii) Describe in words what the numerator and denominator of this fraction represent.
iii) If the fraction represents the loss of the whole original habitat, how much of the original habitat remains?
Answers
1. 8
3. 4
5. 9
7. 4
9. 8
11. 12
13. \(\dfrac{11}{49}\)
15. \(\dfrac{31}{5}\)
17. \(\dfrac{23}{7}\)
19. \(\dfrac{37}{6}\)
21. \(\dfrac{22}{19}\)
23. \(\dfrac{1}{3}\)
25. \(\dfrac{23}{8}\)
27. \(\dfrac{23}{22}\)
29. \(\dfrac{72}{24}\)
31. \(\dfrac{75}{57}\)
33. \(\dfrac{4}{2}\)
35. \(\dfrac{90}{95}\)
37. \(\dfrac{8}{24}\)
39. \(\dfrac{64}{4}\)
41. \(\dfrac{−17}{43}\)
43. \(\dfrac{18}{23}\)
45. \(\dfrac{−46}{41}\)
47. \(\dfrac{− 7}{11}\)
49. \(\dfrac{−11}{49}\)
51. \(\dfrac{−21}{44}\)
53. \(\dfrac{−47}{3}\)
55. \(\dfrac{− 5}{43}\)
57. \(\dfrac{93 n}{62 n}\)
59. \(\dfrac{78 m}{60 m}\)
61. \(\dfrac{75 n}{50 n}\)
63. \(\dfrac{44 m}{4 m}\)
65. \(\dfrac{30 m}{10 m}\)
67. \(\dfrac{30 n}{5 n}\)
69. \(\dfrac{−41 y^4}{24}\)
71. \(\dfrac{− 7x}{4}\)
73. \(− \dfrac{7 y^3}{27}\)
75. \(\dfrac{14}{27 x^2}\)
77. \(− \dfrac{6}{7x}\)
79. \(− \dfrac{37}{11 x}\)
81. \(− \dfrac{6}{49 y}\)
83. \(− \dfrac{x^4}{3}\)
85. \(− \dfrac{13 x^2}{31 y^4}\)
87. \(\dfrac{y^4}{47 x}\)
89. \(− \dfrac{15 y^4 x}{13}\)
91. \(− \dfrac{18}{49xy^3}\)
93. \(− \dfrac{4 x^3}{27 y^2}\)
95. \(−\dfrac{17 x^2}{29 y^4}\)
97. \(− \dfrac{12yx^4}{17}\)
99. \(− \dfrac{13}{4y^2x^3}\)
101.
i) \(\dfrac{1}{2}\)
ii) \(\dfrac{5}{16}\)
iii) \(\dfrac{5}{8}\)


