2.5: Solving Equations Using the Subtraction and Addition Properties of Equality (Part 1)
- Page ID
- 4979
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Determine whether a number is a solution of an equation
- Model the Subtraction Property of Equality
- Solve equations using the Subtraction Property of Equality
- Solve equations using the Addition Property of Equality
- Translate word phrases to algebraic equations
- Translate to an equation and solve
Before you get started, take this readiness quiz.
- Evaluate \(x + 8\) when \(x = 11\). If you missed this problem, review Example 2..2.1.
- Evaluate \(5x − 3\) when \(x = 9\). If you missed this problem, review Example 2.2.2.
- Translate into algebra: the difference of \(x\) and \(8\). If you missed this problem, review Example 2.2.11.
When some people hear the word algebra, they think of solving equations. The applications of solving equations are limitless and extend to all careers and fields. In this section, we will begin solving equations. We will start by solving basic equations, and then as we proceed through the course we will build up our skills to cover many different forms of equations.
Determine Whether a Number is a Solution of an Equation
Solving an equation is like discovering the answer to a puzzle. An algebraic equation states that two algebraic expressions are equal. To solve an equation is to determine the values of the variable that make the equation a true statement. Any number that makes the equation true is called a solution of the equation. It is the answer to the puzzle!
A solution to an equation is a value of a variable that makes a true statement when substituted into the equation. The process of finding the solution to an equation is called solving the equation.
To find the solution to an equation means to find the value of the variable that makes the equation true. Can you recognize the solution of \(x + 2 = 7\)? If you said \(5\), you’re right! We say \(5\) is a solution to the equation \(x + 2 = 7\) because when we substitute \(5\) for \(x\) the resulting statement is true.
\[\begin{split} x + 2 & = 7 \\ 5 + 2 & \stackrel{?}{=} 7 \\ 7 & = 7 \; \checkmark \end{split} \nonumber \]
Since \(5 + 2 = 7\) is a true statement, we know that \(5\) is indeed a solution to the equation. The symbol \(\stackrel{?}{=}\) asks whether the left side of the equation is equal to the right side. Once we know, we can change to an equal sign (\(=\)) or not-equal sign (\(≠\)).
Step 1. Substitute the number for the variable in the equation.
Step 2. Simplify the expressions on both sides of the equation.
Step 3. Determine whether the resulting equation is true.
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
Determine whether \(x = 5\) is a solution of \(6x − 17 = 16\).
Solution
| \(6x − 17 = 16\) | |
| Substitute \(\textcolor{red}{5}\) for x. | \(6 \cdot \textcolor{red}{5} - 17 \stackrel{?}{=} 16\) |
| Multiply. | \(30 - 17 \stackrel{?}{=} 16\) |
| Subtract | \(13 \neq 16\) |
So \(x = 5\) is not a solution to the equation \(6x − 17 = 16\).
Is \(x = 3\) a solution of \(4x − 7 = 16\)?
- Answer
-
no
Is \(x = 2\) a solution of \(6x − 2 = 10\)?
- Answer
-
yes
Determine whether \(y = 2\) is a solution of \(6y − 4 = 5y − 2\).
Solution
Here, the variable appears on both sides of the equation. We must substitute \(2\) for each \(y\).
| \(6y − 4 = 5y − 2\) | |
| Substitute \(\textcolor{red}{2}\) for y. | \(6(\textcolor{red}{2}) - 4 \stackrel{?}{=} 5(\textcolor{red}{2}) - 2\) |
| Multiply. | \(12 - 4 \stackrel{?}{=} 10 - 2\) |
| Subtract | \(8 = 8 \; \checkmark\) |
Since \(y = 2\) results in a true equation, we know that \(2\) is a solution to the equation \(6y − 4 = 5y − 2\).
Is \(y = 3\) a solution of \(9y − 2 = 8y + 1\)?
- Answer
-
yes
Is \(y = 4\) a solution of \(5y − 3 = 3y + 5\)?
- Answer
-
yes
Model the Subtraction Property of Equality
We will use a model to help you understand how the process of solving an equation is like solving a puzzle. An envelope represents the variable – since its contents are unknown – and each counter represents one.
Suppose a desk has an imaginary line dividing it in half. We place three counters and an envelope on the left side of desk, and eight counters on the right side of the desk as in Figure \(\PageIndex{1}\). Both sides of the desk have the same number of counters, but some counters are hidden in the envelope. Can you tell how many counters are in the envelope?
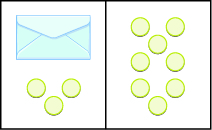
Figure \(\PageIndex{1}\)
What steps are you taking in your mind to figure out how many counters are in the envelope? Perhaps you are thinking “I need to remove the \(3\) counters from the left side to get the envelope by itself. Those \(3\) counters on the left match with \(3\) on the right, so I can take them away from both sides. That leaves five counters on the right, so there must be \(5\) counters in the envelope.” Figure \(\PageIndex{2}\) shows this process.
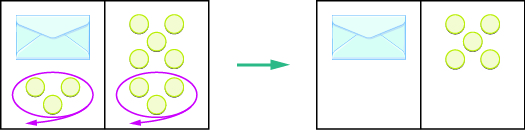
Figure \(\PageIndex{2}\)
What algebraic equation is modeled by this situation? Each side of the desk represents an expression and the center line takes the place of the equal sign. We will call the contents of the envelope \(x\), so the number of counters on the left side of the desk is \(x + 3\). On the right side of the desk are \(8\) counters. We are told that \(x + 3\) is equal to \(8\) so our equation is \(x + 3 = 8\).

Figure \(\PageIndex{3}\)
\(x + 3 = 8\)
Let’s write algebraically the steps we took to discover how many counters were in the envelope.
| \(x + 3 = 8\) | |
| First, we took away three from each side. | \(x + 3 \textcolor{red}{-3} = 8 \textcolor{red}{-3}\) |
| Then we were left with five. | \(x = 5\) |
Now let’s check our solution. We substitute \(5\) for \(x\) in the original equation and see if we get a true statement.
\[\begin{split} x + 3 & = 8 \\ \textcolor{red}{5} + 3 & \stackrel{?}{=} 8 \\ 8 & = 8 \; \checkmark \end{split} \nonumber \]
Our solution is correct. Five counters in the envelope plus three more equals eight
Write an equation modeled by the envelopes and counters, and then solve the equation:
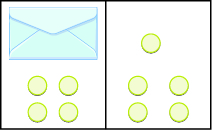
Figure \(\PageIndex{4}\)
Solution
| On the left, write x for the contents of the envelope, add the 4 counters, so we have x + 4. | x + 4 |
| On the right, there are 5 counters. | 5 |
| The two sides are equal. | x + 4 = 5 |
| Solve the equation by subtracting 4 counters from each side. |
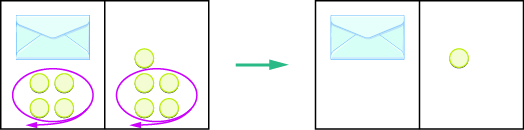
Figure \(\PageIndex{5}\)
We can see that there is one counter in the envelope. This can be shown algebraically as:
\[\begin{split} x + 4 & = 5 \\ x + 4 \textcolor{red}{-4} & = 5 \textcolor{red}{-4} \\ x & = 1 \end{split} \nonumber \]
Substitute \(1\) for \(x\) in the equation to check.
\[\begin{split} x + 4 & = 5 \\ \textcolor{red}{1} + 4 & \stackrel{?}{=} 5 \\ 5 & = 5 \; \checkmark \end{split} \nonumber \]
Since \(x = 1\) makes the statement true, we know that \(1\) is indeed a solution.
Write the equation modeled by the envelopes and counters, and then solve the equation:
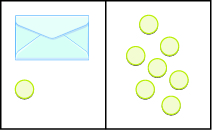
Figure \(\PageIndex{6}\)
- Answer
-
\(x + 1 = 7; x = 6\)
Write the equation modeled by the envelopes and counters, and then solve the equation:
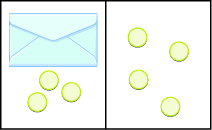
Figure \(\PageIndex{7}\)
- Answer
-
\(x + 3 = 4; x = 1\)
Solve Equations Using the Subtraction Property of Equality
Our puzzle has given us an idea of what we need to do to solve an equation. The goal is to isolate the variable by itself on one side of the equations. In the previous examples, we used the Subtraction Property of Equality, which states that when we subtract the same quantity from both sides of an equation, we still have equality.
For any numbers \(a\), \(b\), and \(c\), if \(a = b\) then \(a − c = b − c\)
Think about twin brothers Andy and Bobby. They are \(17\) years old. How old was Andy \(3\) years ago? He was \(3\) years less than \(17\), so his age was \(17 − 3\), or \(14\). What about Bobby’s age \(3\) years ago? Of course, he was \(14\) also. Their ages are equal now, and subtracting the same quantity from both of them resulted in equal ages \(3\) years ago.
\[\begin{split} a & = b \\ a - 3 & = b - 3 \end{split} \nonumber \]
Step 1. Use the Subtraction Property of Equality to isolate the variable.
Step 2. Simplify the expressions on both sides of the equation.
Step 3. Check the solution.
Solve: \(x + 8 = 17\).
Solution
We will use the Subtraction Property of Equality to isolate \(x\).
| \(x + 8 = 17\) | |
| Subtract 8 from both sides. | \(x + 8 \textcolor{red}{-8} = 17 \textcolor{red}{-8}\) |
| Simplify. | \(x = 9\) |
| Check the solution. | \(\textcolor{red}{9} + 8 = 17\) |
| \(17 = 17 \; \checkmark\) |
Since \(x = 9\) makes \(x + 8 = 17\) a true statement, we know \(9\) is the solution to the equation.
Solve: \(x + 6 = 19\)
- Answer
-
\(x=13\)
Solve: \(x + 9 = 14\)
- Answer
-
\(x=5\)
Solve: \(100 = y + 74\).
Solution
To solve an equation, we must always isolate the variable—it doesn’t matter which side it is on. To isolate y, we will subtract \(74\) from both sides.
| \(100 = y + 74\) | |
| Subtract 74 from both sides. | \(100 \textcolor{red}{-74} = y + 74 \textcolor{red}{-74}\) |
| Simplify. | \(26 = y\) |
| Substitute 26 for y to check | \(100 \stackrel{?}{=} \textcolor{red}{26} + 74\) |
| \(100 = 100 \; \checkmark\) |
Since \(y = 26\) makes \(100 = y + 74\) a true statement, we have found the solution to this equation.
Solve: \(95 = y + 67\)
- Answer
-
\(y=28\)
Solve: \(91 = y + 45\)
- Answer
-
\(y=46\)
Solve Equations Using the Addition Property of Equality
In all the equations we have solved so far, a number was added to the variable on one side of the equation. We used subtraction to “undo” the addition in order to isolate the variable.
But suppose we have an equation with a number subtracted from the variable, such as \(x − 5 = 8\). We want to isolate the variable, so to “undo” the subtraction we will add the number to both sides.
We use the Addition Property of Equality, which says we can add the same number to both sides of the equation without changing the equality. Notice how it mirrors the Subtraction Property of Equality.
For any numbers \(a\), \(b\), and \(c\), if \(a = b\) then \(a + c = b + c\)
Remember the \(17\)-year-old twins, Andy and Bobby? In ten years, Andy’s age will still equal Bobby’s age. They will both be \(27\).
\[\begin{split} a & = b \\ a + 10 & = b + 10 \end{split} \nonumber \]
We can add the same number to both sides and still keep the equality.
Step 1. Use the Addition Property of Equality to isolate the variable.
Step 2. Simplify the expressions on both sides of the equation.
Step 3. Check the solution.
Solve: \(x − 5 = 8\).
Solution
We will use the Addition Property of Equality to isolate the variable.
| \(x − 5 = 8\) | |
| Add 5 to both sides. | \(x − 5 \textcolor{red}{+5} = 8 \textcolor{red}{+5}\) |
| Simplify | \(x = 13\) |
| Now we can check. Let x = \(\textcolor{red}{13}\). | \(\textcolor{red}{13} - 5 \stackrel{?}{=} 8\) |
| \(8 = 8 \; \checkmark\) |
Solve: \(x − 9 = 13\)
- Answer
-
\(x=22\)
Solve: \(y − 1 = 3\)
- Answer
-
\(y=4\)
Solve: \(27 = a − 16\).
Solution
We will add \(16\) to each side to isolate the variable.
| \(27 = a − 16\) | |
| Add 16 to each side. | \(27 \textcolor{red}{+16} = a − 16 \textcolor{red}{+16}\) |
| Simplify. | \(43 = a\) |
| Now we can check. Let a = \(\textcolor{red}{43}\). | \(27 \stackrel{?}{=} \textcolor{red}{43} - 16\) |
| \(27 = 27 \; \checkmark\) |
The solution to \(27 = a − 16\) is \(a = 43\).
Solve: \(19 = a − 18\)
- Answer
-
\(a=37\)
Solve: \(27 = n − 14\)
- Answer
-
\(n=41\)
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


