2.8: Find Multiples and Factors (Part 2)
- Page ID
- 5957
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify Prime and Composite Numbers
Some numbers, like \(72\), have many factors. Other numbers, such as \(7\), have only two factors: \(1\) and the number. A number with only two factors is called a prime number. A number with more than two factors is called a composite number. The number \(1\) is neither prime nor composite. It has only one factor, itself.
A prime number is a counting number greater than \(1\) whose only factors are \(1\) and itself.
A composite number is a counting number that is not prime.
Figure \(\PageIndex{5}\) lists the counting numbers from \(2\) through \(20\) along with their factors. The highlighted numbers are prime, since each has only two factors.
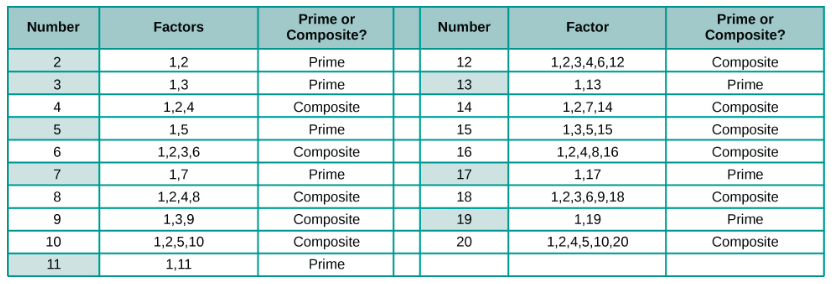
Figure \(\PageIndex{5}\): Factors of the counting numbers from 2 through 20, with prime numbers highlighted
The prime numbers less than \(20\) are \(2\), \(3\), \(5\), \(7\), \(11\), \(13\), \(17\), and \(19\). There are many larger prime numbers too. In order to determine whether a number is prime or composite, we need to see if the number has any factors other than \(1\) and itself. To do this, we can test each of the smaller prime numbers in order to see if it is a factor of the number. If none of the prime numbers are factors, then that number is also prime.
- Step 1. Test each of the primes, in order, to see if it is a factor of the number.
- Step 2. Start with \(2\) and stop when the quotient is smaller than the divisor or when a prime factor is found.
- Step 3. If the number has a prime factor, then it is a composite number. If it has no prime factors, then the number is prime.
Identify each number as prime or composite:
- \(83\)
- \(77\)
Solution
- Test each prime, in order, to see if it is a factor of \(83\), starting with \(2\), as shown. We will stop when the quotient is smaller than the divisor.
| Prime | Test | Factor of 83? |
|---|---|---|
| 2 | Last digit of 83 is not 0, 2, 4, 6, or 8. | No. |
| 3 | 8 + 3 = 11, and 11 is not divisible by 3. | No. |
| 5 | The last digit of 83 is not 5 or 0. | No. |
| 7 | 83 ÷ 7 = 11.857…. | No. |
| 11 | 83 ÷ 11 = 7.545… | No. |
We can stop when we get to \(11\) because the quotient (\(7.545…\)) is less than the divisor. We did not find any prime numbers that are factors of \(83\), so we know \(83\) is prime.
- Test each prime, in order, to see if it is a factor of \(77\).
| Prime | Test | Factor of 77? |
|---|---|---|
| 2 | Last digit is not 0, 2, 4, 6, or 8. | No. |
| 3 | 7 + 7 = 14, and 14 is not divisible by 3. | No. |
| 5 | The last digit is not 5 or 0. | No. |
| 7 | 77 ÷ 7 = 11 | Yes. |
Since \(77\) is divisible by \(7\), we know it is not a prime number. It is composite.
Identify the number as prime or composite: \(91\)
- Answer
-
composite
Identify the number as prime or composite: \(137\)
- Answer
-
prime
Access Additional Online Resources
Key Concepts
| Divisibility Tests | |
|---|---|
| A number is divisible by | |
| 2 | if the last digit is 0, 2, 4, 6, or 8 |
| 3 | if the sum of the digits is divisible by 3 |
| 5 | if the last digit is 5 or 0 |
| 6 | if divisible by both 2 and 3 |
| 10 | if the last digit is 0 |
- Factors If \(a\cdot b = m\), then \(a\) and \(b\) are factors of \(m\), and \(m\) is the product of \(a\) and \(b\).
- Find all the factors of a counting number.
- Divide the number by each of the counting numbers, in order, until the quotient is smaller than the divisor.
- If the quotient is a counting number, the divisor and quotient are a pair of factors.
- If the quotient is not a counting number, the divisor is not a factor.
- List all the factor pairs.
- Write all the factors in order from smallest to largest.
- Divide the number by each of the counting numbers, in order, until the quotient is smaller than the divisor.
- Determine if a number is prime.
- Test each of the primes, in order, to see if it is a factor of the number.
- Start with \(2\) and stop when the quotient is smaller than the divisor or when a prime factor is found.
- If the number has a prime factor, then it is a composite number. If it has no prime factors, then the number is prime.
Glossary
- multiple of a number
-
A number is a multiple of \(n\) if it is the product of a counting number and \(n\)
- divisibility
-
If a number \(m\) is a multiple of \(n\), then we say that \(m\) is divisible by \(n\).
- prime number
-
A prime number is a counting number greater than \(1\) whose only factors are \(1\) and itself.
- composite number
-
A composite number is a counting number that is not prime.
Practice Makes Perfect
Identify Multiples of Numbers
In the following exercises, list all the multiples less than 50 for the given number.
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 12
Use Common Divisibility Tests
In the following exercises, use the divisibility tests to determine whether each number is divisible by 2, 3, 4, 5, 6, and 10.
- 84
- 96
- 75
- 78
- 168
- 264
- 900
- 800
- 896
- 942
- 375
- 750
- 350
- 550
- 1430
- 1080
- 22,335
- 39,075
Find All the Factors of a Number
In the following exercises, find all the factors of the given number.
- 36
- 42
- 60
- 48
- 144
- 200
- 588
- 576
Identify Prime and Composite Numbers
In the following exercises, determine if the given number is prime or composite.
- 43
- 67
- 39
- 53
- 71
- 119
- 481
- 221
- 209
- 359
- 667
- 1771
Everyday Math
- Banking Frank’s grandmother gave him $100 at his high school graduation. Instead of spending it, Frank opened a bank account. Every week, he added $15 to the account. The table shows how much money Frank had put in the account by the end of each week. Complete the table by filling in the blanks.
| Weeks after graduation | Total number of dollars Frank put in the account | Simplified Total |
|---|---|---|
| 0 | 100 | 100 |
| 1 | 100 + 15 | 115 |
| 2 | 100 + 15 • 2 | 130 |
| 3 | 100 + 15 • 3 | |
| 4 | 100 + 15 • [] | |
| 5 | 100 + [] | |
| 6 | ||
| 20 | ||
| x |
- Banking In March, Gina opened a Christmas club savings account at her bank. She deposited $75 to open the account. Every week, she added $20 to the account. The table shows how much money Gina had put in the account by the end of each week. Complete the table by filling in the blanks.
| Weeks after opening the account | Total number of dollars Gina put in the account | Simplified Total |
|---|---|---|
| 0 | 75 | 75 |
| 1 | 75 + 20 | 95 |
| 2 | 75 + 20 • 2 | 115 |
| 3 | 75 + 20 • 3 | |
| 4 | 75 + 20 • [] | |
| 5 | 75 + [] | |
| 6 | ||
| 20 | ||
| x |
Writing Exercises
- If a number is divisible by 2 and by 3, why is it also divisible by 6?
- What is the difference between prime numbers and composite numbers?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


