3.E: Integers (Exercises)
- Page ID
- 6044
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)3.1 - Introduction to Integers
Locate Positive and Negative Numbers on the Number Line
In the following exercises, locate and label the integer on the number line.
- 5
- −5
- −3
- 3
- −8
- −7
Order Positive and Negative Numbers
In the following exercises, order each of the following pairs of numbers, using < or >.
- 4__8
- −6__3
- −5__−10
- −9__−4
- 2__−7
- −3__1
Find Opposites
In the following exercises, find the opposite of each number.
- 6
- −2
- −4
- 3
In the following exercises, simplify.
- (a) −(8) (b) −(−8)
- (a) −(9) (b) −(−9)
In the following exercises, evaluate.
- −x, when (a) x = 32 (b) x = −32
- −n, when (a) n = 20 (b) n = −20
Simplify Absolute Values
In the following exercises, simplify.
- |−21|
- |−42|
- |36|
- −|15|
- |0|
- −|−75|
In the following exercises, evaluate.
- |x| when x = −14
- −|r| when r = 27
- −|−y| when y = 33
- |−n| when n = −4
In the following exercises, fill in <, >, or = for each of the following pairs of numbers.
- −|−4|__4
- −2__|−2|
- −|−6|__−6
- −|−9|__|−9|
In the following exercises, simplify.
- −(−55) and − |−55|
- −(−48) and − |−48|
- |12 − 5|
- |9 + 7|
- 6|−9|
- |14−8| − |−2|
- |9 − 3| − |5 − 12|
- 5 + 4|15 − 3|
Translate Phrases to Expressions with Integers
In the following exercises, translate each of the following phrases into expressions with positive or negative numbers.
- the opposite of 16
- the opposite of −8
- negative 3
- 19 minus negative 12
- a temperature of 10 below zero
- an elevation of 85 feet below sea level
3.2 - Add Integers
Model Addition of Integers
In the following exercises, model the following to find the sum.
- 3 + 7
- −2 + 6
- 5 + (−4)
- −3 + (−6)
Simplify Expressions with Integers
In the following exercises, simplify each expression.
- 14 + 82
- −33 + (−67)
- −75 + 25
- 54 + (−28)
- 11 + (−15) + 3
- −19 + (−42) + 12
- −3 + 6(−1 + 5)
- 10 + 4(−3 + 7)
Evaluate Variable Expressions with Integers
In the following exercises, evaluate each expression.
- n + 4 when (a) n = −1 (b) n = −20
- x + (−9) when (a) x = 3 (b) x = −3
- (x + y)3 when x = −4, y = 1
- (u + v)2 when u = −4, v = 11
Translate Word Phrases to Algebraic Expressions
In the following exercises, translate each phrase into an algebraic expression and then simplify.
- the sum of −8 and 2
- 4 more than −12
- 10 more than the sum of −5 and −6
- the sum of 3 and −5, increased by 18
Add Integers in Applications
In the following exercises, solve.
- Temperature On Monday, the high temperature in Denver was −4 degrees. Tuesday’s high temperature was 20 degrees more. What was the high temperature on Tuesday?
- Credit Frida owed $75 on her credit card. Then she charged $21 more. What was her new balance?
3.3 - Subtract Integers
Model Subtraction of Integers
In the following exercises, model the following.
- 6 − 1
- −4 − (−3)
- 2 − (−5)
- −1 − 4
Simplify Expressions with Integers
In the following exercises, simplify each expression.
- 24 − 16
- 19 − (−9)
- −31 − 7
- −40 − (−11)
- −52 − (−17) − 23
- 25 − (−3 − 9)
- (1 − 7) − (3 − 8)
- 32 − 72
Evaluate Variable Expressions with Integers
In the following exercises, evaluate each expression.
- x − 7 when (a) x = 5 (b) x = −4
- 10 − y when (a) y = 15 (b) y = −16
- 2n2 − n + 5 when n = −4
- −15 − 3u2 when u = −5
Translate Phrases to Algebraic Expressions
In the following exercises, translate each phrase into an algebraic expression and then simplify.
- the difference of −12 and 5
- subtract 23 from −50
Subtract Integers in Applications
In the following exercises, solve the given applications.
- Temperature One morning the temperature in Bangor, Maine was 18 degrees. By afternoon, it had dropped 20 degrees. What was the afternoon temperature?
- Temperature On January 4, the high temperature in Laredo, Texas was 78 degrees, and the high in Houlton, Maine was −28 degrees. What was the difference in temperature of Laredo and Houlton?
3.4 - Multiply and Divide Integers
Multiply Integers
In the following exercises, multiply.
- −9 • 4
- 5(−7)
- (−11)(−11)
- −1 • 6
Divide Integers
In the following exercises, divide.
- 56 ÷ (−8)
- −120 ÷ (−6)
- −96 ÷ 12
- 96 ÷ (−16)
- 45 ÷ (−1)
- −162 ÷ (−1)
Simplify Expressions with Integers
In the following exercises, simplify each expression.
- 5(−9) − 3(−12)
- (−2)5
- −34
- (−3)(4)(−5)(−6)
- 42 − 4(6 − 9)
- (8 − 15)(9 − 3)
- −2(−18) ÷ 9
- 45 ÷ (−3) − 12
Evaluate Variable Expressions with Integers
In the following exercises, evaluate each expression.
- 7x − 3 when x = −9
- 16 − 2n when n = −8
- 5a + 8b when a = −2, b = −6
- x2 + 5x + 4 when x = −3
Translate Word Phrases to Algebraic Expressions
In the following exercises, translate to an algebraic expression and simplify if possible.
- the product of −12 and 6
- the quotient of 3 and the sum of −7 and s
3.5 - Solve Equations using Integers; The Division Property of Equality
Determine Whether a Number is a Solution of an Equation
In the following exercises, determine whether each number is a solution of the given equation.
- 5x − 10 = −35
- x = −9
- x = −5
- x = 5
- 8u + 24 = −32
- u = −7
- u = −1
- u = 7
Using the Addition and Subtraction Properties of Equality
In the following exercises, solve.
- a + 14 = 2
- b − 9 = −15
- c + (−10) = −17
- d − (−6) = −26
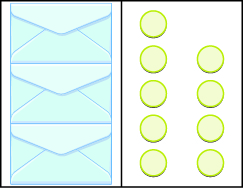
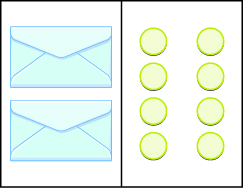
Model the Division Property of Equality
In the following exercises, write the equation modeled by the envelopes and counters. Then solve it.
Solve Equations Using the Division Property of Equality
In the following exercises, solve each equation using the division property of equality and check the solution.
- 8p = 72
- −12q = 48
- −16r = −64
- −5s = −100
Translate to an Equation and Solve.
In the following exercises, translate and solve.
- The product of −6 and y is −42
- The difference of z and −13 is −18.
- Four more than m is −48.
- The product of −21 and n is 63.
Everyday Math
- Describe how you have used two topics from this chapter in your life outside of your math class during the past month.
PRACTICE TEST
- Locate and label 0, 2, −4, and −1 on a number line.
In the following exercises, compare the numbers, using < or > or =.
- (a) −6__3 (b) −1__−4
- (a) −5__|−5| (b) −|−2|__−2
In the following exercises, find the opposite of each number.
- (a) −7 (b) 8
In the following exercises, simplify.
- −(−22)
- |4 − 9|
- −8 + 6
- −15 + (−12)
- −7 − (−3)
- 10 − (5 − 6)
- −3 • 8
- −6(−9)
- 70 ÷ (−7)
- (−2)3
- −42
- 16−3(5−7)
- |21 − 6| − |−8|
In the following exercises, evaluate.
- 35 − a when a = −4
- (−2r)2 when r = 3
- 3m − 2n when m = 6, n = −8
- −|−y| when y = 17
In the following exercises, translate each phrase into an algebraic expression and then simplify, if possible.
- the difference of −7 and −4
- the quotient of 25 and the sum of m and n.
In the following exercises, solve.
- Early one morning, the temperature in Syracuse was −8°F. By noon, it had risen 12°. What was the temperature at noon?
- Collette owed $128 on her credit card. Then she charged $65. What was her new balance?
In the following exercises, solve.
- n + 6 = 5
- p − 11 = −4
- −9r = −54
In the following exercises, translate and solve.
- The product of 15 and x is 75.
- Eight less than y is −32.