4.E: Fractions (Exercises)

Last updated
Save as PDF

Page ID: 6074

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

4.1 - Visualize Fractions

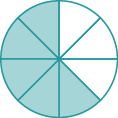
In the following exercises, name the fraction of each figure that is shaded.

$A circle is shown. It is divided into 8 equal pieces. 5 pieces are shaded.$
$A square is shown. It is divided into 9 equal pieces. 5 pieces are shaded.$

In the following exercises, name the improper fractions. Then write each improper fraction as a mixed number.

$Two squares are shown. Both are divided into four equal pieces. The square on the left has all 4 pieces shaded. The square on the right has one piece shaded.$
$Two circles are shown. Both are divided into two equal pieces. The circle on the left has both pieces shaded. The circle on the right has one piece shaded.$

In the following exercises, convert the improper fraction to a mixed number.

$\dfrac{58}{15}$
$\dfrac{63}{11}$

In the following exercises, convert the mixed number to an improper fraction.

$12 \dfrac{1}{4}$
$9 \dfrac{4}{5}$
Find three fractions equivalent to $\dfrac{2}{5}$. Show your work, using figures or algebra.
Find three fractions equivalent to $− \dfrac{4}{3}$. Show your work, using figures or algebra.

In the following exercises, locate the numbers on a number line.

$\dfrac{5}{8}, \dfrac{4}{3}, 3 \dfrac{3}{4}$, 4
$\dfrac{1}{4}, − \dfrac{1}{4}, 1 \dfrac{1}{3}, −1 \dfrac{1}{3}, \dfrac{7}{2}, − \dfrac{7}{2}$

In the following exercises, order each pair of numbers, using < or >.

−1___$− \dfrac{2}{5}$
$−2 \dfrac{1}{2}$___−3

4.2 - Multiply and Divide Fractions

In the following exercises, simplify.

$− \dfrac{63}{84}$
$− \dfrac{90}{120}$
$− \dfrac{14a}{14b}$
$− \dfrac{8x}{8y}$

In the following exercises, multiply.

$\dfrac{2}{5} \cdot \dfrac{8}{13}$
$− \dfrac{1}{3} \cdot \dfrac{12}{7}$
$\dfrac{2}{9} \cdot \left(− \dfrac{45}{32}\right)$
6m $\cdot \dfrac{4}{11}$
$− \dfrac{1}{4}$ (−32)
$3 \dfrac{1}{5} \cdot 1 \dfrac{7}{8}$

In the following exercises, find the reciprocal.

$\dfrac{2}{9}$
$\dfrac{15}{4}$
3
$− \dfrac{1}{4}$
Fill in the chart.

	Opposite	Absolute Value	Reciprocal
$- \dfrac{5}{13}$
$\dfrac{3}{10}$
$\dfrac{9}{4}$
-12

In the following exercises, divide.

$\dfrac{2}{3} \div \dfrac{1}{6}$
$\left(− \dfrac{3x}{5}\right) \div \left(− \dfrac{2y}{3}\right)$
$\dfrac{4}{5} \div$ 3
8 $\div 2 \dfrac{2}{3}$
$8 \dfrac{2}{3} \div 1 \dfrac{1}{12}$

4.3 - Multiply and Divide Mixed Numbers and Complex Fractions

In the following exercises, perform the indicated operation.

$3 \dfrac{1}{5} \cdot 1 \dfrac{7}{8}$
$−5 \dfrac{7}{12} \cdot 4 \dfrac{4}{11}$
8 $\div 2 \dfrac{2}{3}$
$8 \dfrac{2}{3} \div 1 \dfrac{1}{12}$

In the following exercises, translate the English phrase into an algebraic expression.

the quotient of 8 and y
the quotient of V and the difference of h and 6

In the following exercises, simplify the complex fraction.

$\dfrac{\dfrac{5}{8}}{\dfrac{4}{5}}$
$\dfrac{\dfrac{8}{9}}{−4}$
$\dfrac{\dfrac{n}{4}}{\dfrac{3}{8}}$
$\dfrac{−1 \dfrac{5}{6}}{− \dfrac{1}{12}}$

In the following exercises, simplify.

$\dfrac{5 + 16}{5}$
$\dfrac{8 \cdot 4 − 5^{2}}{3 \cdot 12}$
$\dfrac{8 \cdot 7 + 5(8 − 10)}{9 \cdot 3 − 6 \cdot 4}$

4.4 - Add and Subtract Fractions with Common Denominators

In the following exercises, add.

$\dfrac{3}{8} + \dfrac{2}{8}$
$\dfrac{4}{5} + \dfrac{1}{5}$
$\dfrac{2}{5} + \dfrac{1}{5}$
$\dfrac{15}{32} + \dfrac{9}{32}$
$\dfrac{x}{10} + \dfrac{7}{10}$

In the following exercises, subtract.

$\dfrac{8}{11} − \dfrac{6}{11}$
$\dfrac{11}{12} − \dfrac{5}{12}$
$\dfrac{4}{5} − \dfrac{y}{5}$
$− \dfrac{31}{30} − \dfrac{7}{30}$
$\dfrac{3}{2} − \left(\dfrac{3}{2}\right)$
$\dfrac{11}{15} − \dfrac{5}{15} − \left(− \dfrac{2}{15}\right)$

4.5 - Add and Subtract Fractions with Different Denominators

In the following exercises, find the least common denominator.

$\dfrac{1}{3}$ and $\dfrac{1}{12}$
$\dfrac{1}{3}$ and $\dfrac{4}{5}$
$\dfrac{8}{15}$ and $\dfrac{11}{20}$
$\dfrac{3}{4}, \dfrac{1}{6}$, and $\dfrac{5}{10}$

In the following exercises, change to equivalent fractions using the given LCD.

$\dfrac{1}{3}$ and $\dfrac{1}{5}$, LCD = 15
$\dfrac{3}{8}$ and $\dfrac{5}{6}$, LCD = 24
$− \dfrac{9}{16}$ and $\dfrac{5}{12}$, LCD = 48
$\dfrac{1}{3}, \dfrac{3}{4}$ and $\dfrac{4}{5}$, LCD = 60

In the following exercises, perform the indicated operations and simplify.

$\dfrac{1}{5} + \dfrac{2}{3}$
$\dfrac{11}{12} − \dfrac{2}{3}$
$− \dfrac{9}{10} − \dfrac{3}{4}$
$− \dfrac{11}{36} − \dfrac{11}{20}$
$− \dfrac{22}{25} + \dfrac{9}{40}$
$\dfrac{y}{10} − \dfrac{1}{3}$
$\dfrac{2}{5} + \left(− \dfrac{5}{9}\right)$
$\dfrac{4}{11} \div \dfrac{2}{7d}$
$\dfrac{2}{5} + \left(− \dfrac{3n}{8}\right) \left(− \dfrac{2}{9n}\right)$
$\dfrac{\left(\dfrac{2}{3}\right)^{2}}{\left(\dfrac{5}{8}\right)^{2}}$
$\left(\dfrac{11}{12} + \dfrac{3}{8}\right) \div \left(\dfrac{5}{6} − \dfrac{1}{10}\right)$

In the following exercises, evaluate.

y − $\dfrac{4}{5}$ when (a) y = $− \dfrac{4}{5}$ (b) y = $\dfrac{1}{4}$
6mn² when m = $\dfrac{3}{4}$ and n = $− \dfrac{1}{3}$

4.6 - Add and Subtract Mixed Numbers

In the following exercises, perform the indicated operation.

$4 \dfrac{1}{3} + 9 \dfrac{1}{3}$
$6 \dfrac{2}{5} + 7 \dfrac{3}{5}$
$5 \dfrac{8}{11} + 2 \dfrac{4}{11}$
$3 \dfrac{5}{8} + 3 \dfrac{7}{8}$
$9 \dfrac{13}{20} − 4 \dfrac{11}{20}$
$2 \dfrac{3}{10} − 1 \dfrac{9}{10}$
$2 \dfrac{11}{12} − 1 \dfrac{7}{12}$
$8 \dfrac{6}{11} − 2 \dfrac{9}{11}$

4.7 - Solve Equations with Fractions

In the following exercises, determine whether the each number is a solution of the given equation.

x − $\dfrac{1}{2}$ = $\dfrac{1}{6}$:
1. x = 1
2. x = $\dfrac{2}{3}$
3. x = $− \dfrac{1}{3}$
y + $\dfrac{3}{5}$ = $\dfrac{5}{9}$:
1. y = $\dfrac{1}{2}$
2. y = $\dfrac{52}{45}$
3. y = $− \dfrac{2}{45}$

In the following exercises, solve the equation.

n + $\dfrac{9}{11}$ = $\dfrac{4}{11}$
x − $\dfrac{1}{6}$ = $\dfrac{7}{6}$
h − $\left(- \dfrac{7}{8}\right)$ = $− \dfrac{2}{5}$
$\dfrac{x}{5}$ = −10
−z = 23

In the following exercises, translate and solve.

The sum of two-thirds and n is $− \dfrac{3}{5}$.
The difference of q and one-tenth is $\dfrac{1}{2}$.
The quotient of p and −4 is −8.
Three-eighths of y is 24.

PRACTICE TEST

Convert the improper fraction to a mixed number.

$\dfrac{19}{5}$

Convert the mixed number to an improper fraction.

$3 \dfrac{2}{7}$

Locate the numbers on a number line.

$\dfrac{1}{2}, 1 \dfrac{2}{3}, −2 \dfrac{3}{4}$, and $\dfrac{9}{4}$

In the following exercises, simplify.

$\dfrac{5}{20}$
$\dfrac{18r}{27s}$
$\dfrac{1}{3} \cdot \dfrac{3}{4}$
$\dfrac{3}{5} \cdot$ 15
−36u$\left(− \dfrac{4}{9}\right)$
$−5 \dfrac{7}{12} \cdot 4 \dfrac{4}{11}$
$− \dfrac{5}{6} \div \dfrac{5}{12}$
$\dfrac{7}{11} \div \left(− \dfrac{7}{11}\right)$
$\dfrac{9a}{10} \div \dfrac{15a}{8}$
$−6 \dfrac{2}{5} \div$ 4
$\left(−15 \dfrac{5}{6}\right) \div \left(−3 \dfrac{1}{6}\right)$
$\dfrac{−6}{\dfrac{6}{11}}$
$\dfrac{\dfrac{p}{2}}{\dfrac{q}{5}}$
$\dfrac{− \dfrac{4}{15}}{−2 \dfrac{2}{3}}$
$\dfrac{9^{2} − 4^{2}}{9 − 4}$
$\dfrac{2}{d} + \dfrac{9}{d}$
$− \dfrac{3}{13} + \left(− \dfrac{4}{13}\right)$
$− \dfrac{22}{25} + \dfrac{9}{40}$
$\dfrac{2}{5} + \left(− \dfrac{7}{5}\right)$
$− \dfrac{3}{10} + \left(- \dfrac{5}{8}\right)$
$− \dfrac{3}{4} \div \dfrac{x}{3}$
$\dfrac{2^{3} − 2^{2}}{\left(\dfrac{3}{4}\right)^{2}}$
$\dfrac{\dfrac{5}{14} + \dfrac{1}{8}}{\dfrac{9}{56}}$

Evaluate.

x + $\dfrac{1}{3}$ when (a) x = $\dfrac{2}{3}$ (b) x = $− \dfrac{5}{6}$

In the following exercises, solve the equation.

y + $\dfrac{3}{5}$ = $\dfrac{7}{5}$
a − $\dfrac{3}{10}$ = $− \dfrac{9}{10}$
f + $\left(− \dfrac{2}{3}\right)$ = $\dfrac{5}{12}$
$\dfrac{m}{−2}$ = −16
$− \dfrac{2}{3}$c = 18
Translate and solve: The quotient of p and −4 is −8. Solve for p.

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."

Search

Text Color

Text Size

Margin Size

Font Type