5.12: Simplify and Use Square Roots (Part 1)
- Page ID
- 6456
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Simplify expressions with square roots
- Estimate square roots
- Approximate square roots
- Simplify variable expressions with square roots
- Use square roots in applications
Before you get started, take this readiness quiz.
- Simplify: (−9)2. If you missed this problem, review Example 3.7.6.
- Round 3.846 to the nearest hundredth. If you missed this problem, review Example 5.2.9.
- Evaluate 12d for d = 80. If you missed this problem, review Example 2.3.2.
Simplify Expressions with Square Roots
To start this section, we need to review some important vocabulary and notation. Remember that when a number n is multiplied by itself, we can write this as n2, which we read aloud as “n squared.” For example, 82 is read as “8 squared.” We call 64 the square of 8 because 82 = 64. Similarly, 121 is the square of 11, because 112 = 121.
If n2 = m, then m is the square of n.
Modeling Squares
Do you know why we use the word square? If we construct a square with three tiles on each side, the total number of tiles would be nine.
This is why we say that the square of three is nine.
\[3^{2} = 9\]
The number 9 is called a perfect square because it is the square of a whole number.
The chart shows the squares of the counting numbers 1 through 15. You can refer to it to help you identify the perfect squares.

A perfect square is the square of a whole number.
What happens when you square a negative number?
\[\begin{split} (-8)^{2} & = (-8) (-8) \\ & = 64 \end{split}\]
When we multiply two negative numbers, the product is always positive. So, the square of a negative number is always positive. The chart shows the squares of the negative integers from −1 to −15.

Did you notice that these squares are the same as the squares of the positive numbers?
Square Roots
Sometimes we will need to look at the relationship between numbers and their squares in reverse. Because 102 = 100, we say 100 is the square of 10. We can also say that 10 is a square root of 100.
A number whose square is m is called a square root of m. If n2 = m, then n is a square root of m.
Notice (−10)2 = 100 also, so −10 is also a square root of 100. Therefore, both 10 and −10 are square roots of 100. So, every positive number has two square roots: one positive and one negative.
What if we only want the positive square root of a positive number? The radical sign, \(\sqrt{\quad}\), stands for the positive square root. The positive square root is also called the principal square root.
\(\sqrt{m}\) is read as “the square root of m.” If m = n2, then m = n for n ≥ 0.
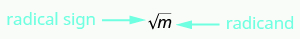
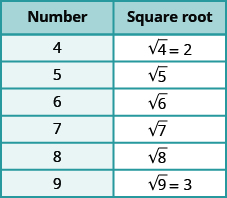
We can also use the radical sign for the square root of zero. Because 02 = 0, \(\sqrt{0}\) = 0. Notice that zero has only one square root. The chart shows the square roots of the first 15 perfect square numbers.

Simplify: (a) \(\sqrt{25}\) (b) \(\sqrt{121}\).
Solution
(a) \(\sqrt{25}\)
| Since 52 = 25 | 5 |
(b) \(\sqrt{121}\)
| Since 112 = 121 | 11 |
Simplify: (a) \(\sqrt{36}\) (b) \(\sqrt{169}\).
- Answer a
-
6
- Answer b
-
13
Simplify: (a) \(\sqrt{16}\) (b) \(\sqrt{196}\).
- Answer a
-
4
- Answer b
-
14
Every positive number has two square roots and the radical sign indicates the positive one. We write \(\sqrt{100}\) = 10. If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example, \(− \sqrt{100}\) = −10.
Simplify. (a) \(- \sqrt{9}\) (b) \(- \sqrt{144}\).
Solution
(a) \(- \sqrt{9}\)
| The negative is in front of the radical sign. | -3 |
(b) \(- \sqrt{144}\)
| The negative is in front of the radical sign. | -12 |
Simplify: (a) \(- \sqrt{4}\) (b) \(- \sqrt{225}\).
- Answer a
-
-2
- Answer b
-
-15
Simplify: (a) \(- \sqrt{81}\) (b) \(- \sqrt{64}\).
- Answer a
-
-9
- Answer b
-
-8
Square Root of a Negative Number
Can we simplify \(\sqrt{−25}\)? Is there a number whose square is −25?
\[(\;)^{2} = -25?\]
None of the numbers that we have dealt with so far have a square that is −25. Why? Any positive number squared is positive, and any negative number squared is also positive. In the next chapter we will see that all the numbers we work with are called the real numbers. So we say there is no real number equal to \(\sqrt{−25}\). If we are asked to find the square root of any negative number, we say that the solution is not a real number.
Simplify: (a) \(\sqrt{−169}\) (b) \(− \sqrt{121}\).
Solution
(a) There is no real number whose square is −169. Therefore, \(\sqrt{−169}\) is not a real number.
(b) The negative is in front of the radical sign, so we find the opposite of the square root of 121.
| The negative is in front of the radical. | -11 |
Simplify: (a) \(\sqrt{-196}\) (b) \(- \sqrt{81}\).
- Answer a
-
not a real number
- Answer b
-
-9
Simplify: (a) \(- \sqrt{49}\) (b) \(\sqrt{-121}\).
- Answer a
-
-7
- Answer b
-
not a real number
Square Roots and the Order of Operations
When using the order of operations to simplify an expression that has square roots, we treat the radical sign as a grouping symbol. We simplify any expressions under the radical sign before performing other operations.
Simplify: (a) \(\sqrt{25} + \sqrt{144}\) (b) \(\sqrt{25 + 144}\).
Solution
(a)
| Use the order of operations. | $$\sqrt{25} + \sqrt{144}$$ |
| Simplify each radical. | 5 + 12 |
| Add. | 17 |
(b)
| Use the order of operations. | $$\sqrt{25 + 144}$$ |
| Add under the radical sign. | $$\sqrt{169}$$ |
| Simplify. | 13 |
Simplify: (a) \(\sqrt{9} + \sqrt{16}\) (b) \(\sqrt{9 + 16}\).
- Answer a
-
7
- Answer b
-
5
Simplify: (a) \(\sqrt{64 + 225}\) (b) \(\sqrt{64} + \sqrt{225}\).
- Answer a
-
17
- Answer b
-
23
Notice the different answers in parts (a) and (b) of Example \(\PageIndex{4}\). It is important to follow the order of operations correctly. In (a), we took each square root first and then added them. In (b), we added under the radical sign first and then found the square root.
Estimate Square Roots
So far we have only worked with square roots of perfect squares. The square roots of other numbers are not whole numbers.
We might conclude that the square roots of numbers between 4 and 9 will be between 2 and 3, and they will not be whole numbers. Based on the pattern in the table above, we could say that \(\sqrt{5}\) is between 2 and 3. Using inequality symbols, we write
\[2 < \sqrt{5} < 3\]
Estimate \(\sqrt{60}\) between two consecutive whole numbers.
Solution
Think of the perfect squares closest to 60. Make a small table of these perfect squares and their squares roots.

| Locate 60 between two consecutive perfect squares. | 49 < 60 < 64 |
| \(\sqrt{60}\) is between their square roots. | $$7 < \sqrt{60} < 8$$ |
Estimate \(\sqrt{38}\) between two consecutive whole numbers.
- Answer
-
\(6 < \sqrt{38} < 7 \)
Estimate \(\sqrt{84}\) between two consecutive whole numbers.
- Answer
-
\(9 < \sqrt{84} < 10 \)
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


