6.2: Solve General Applications of Percent
- Page ID
- 5027
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Translate and solve basic percent equations
- Solve applications of percent
- Find percent increase and percent decrease
Before you get started, take this readiness quiz.
- Translate and solve: \(\dfrac{3}{4}\) of x is 24. If you missed this problem, review Example 4.13.11.
- Simplify: (4.5)(2.38). If you missed this problem, review Example 5.3.5.
- Solve: 3.5 = 0.7n. If you missed this problem, review Example 5.7.4.
Translate and Solve Basic Percent Equations
We will solve percent equations by using the methods we used to solve equations with fractions or decimals. In the past, you may have solved percent problems by setting them up as proportions. That was the best method available when you did not have the tools of algebra. Now as a prealgebra student, you can translate word sentences into algebraic equations, and then solve the equations.
We'll look at a common application of percent—tips to a server at a restaurant—to see how to set up a basic percent application.
When Aolani and her friends ate dinner at a restaurant, the bill came to $80. They wanted to leave a 20% tip. What amount would the tip be? To solve this, we want to find what amount is 20% of $80. The $80 is called the base. The amount of the tip would be 0.20(80), or $16 See Figure \(\PageIndex{1}\). To find the amount of the tip, we multiplied the percent by the base.

Figure \(\PageIndex{1}\) - A 20% tip for an $80 restaurant bill comes out to $16.
In the next examples, we will find the amount. We must be sure to change the given percent to a decimal when we translate the words into an equation.
What number is 35% of 90?
Solution
| Translate into algebra. Let n = the number. | 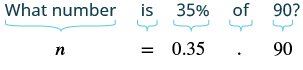 |
| Multiply. | n = 31.5 |
31.5 is 35% of 90
What number is 45% of 80?
- Answer
-
36
What number is 55% of 60?
- Answer
- 33
125% of 28 is what number?
Solution
| Translate into algebra. Let a = the number. | 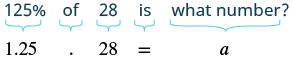 |
| Multiply. | 35 = a |
125% of 28 is 35
Remember that a percent over 100 is a number greater than 1. We found that 125% of 28 is 35, which is greater than 28.
150% of 78 is what number?
- Answer
- 117
175% of 72 is what number?
- Answer
- 126
In the next examples, we are asked to find the base.
Translate and solve: 36 is 75% of what number?
Solution
| Translate. Let b = the number. | 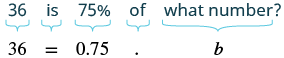 |
| Divide both sides by 0.75. | $$\dfrac{36}{0.75} = \dfrac{0.75b}{0.75}$$ |
| Simplify. | 48 = b |
36 is 75% of 48
17 is 25% of what number?
- Answer
- 68
40 is 62.5% of what number?
- Answer
- 64
6.5% of what number is $1.17?
Solution
| Translate. Let b = the number. | 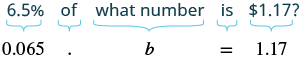 |
| Divide both sides by 0.065. | $$\dfrac{0.065n}{0.065} = \dfrac{1.17}{0.065}$$ |
| Simplify. | n = 18 |
6.5% of $18 is $1.17.
7.5% of what number is $1.95?
- Answer
- $26
8.5% of what number is $3.06?
- Answer
- $36
In the next examples, we will solve for the percent.
What percent of 36 is 9?
Solution
| Translate into algebra. Let p = the percent. |  |
| Divide by 36. | $$\dfrac{36p}{36} = \dfrac{9}{36}$$ |
| Simplify. | $$p = \dfrac{1}{4}$$ |
| Convert to decimal form. | p = 0.25 |
| Convert to percent. | p = 25% |
25% of 36 is 9.
What percent of 76 is 57?
- Answer
- 75%
What percent of 120 is 96?
- Answer
- 80%
144 is what percent of 96?
Solution
| Translate into algebra. Let p = the percent. | 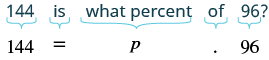 |
| Divide by 96. | $$\dfrac{144}{96} = \dfrac{96p}{96}$$ |
| Simplify. | 1.5 = p |
| Convert to percent. | 150% = p |
144 is 150% of 96.
110 is what percent of 88?
- Answer
- 125%
126 is what percent of 72?
- Answer
- 175%
Solve Applications of Percent
Many applications of percent occur in our daily lives, such as tips, sales tax, discount, and interest. To solve these applications we'll translate to a basic percent equation, just like those we solved in the previous examples in this section. Once you translate the sentence into a percent equation, you know how to solve it.
We will update the strategy we used in our earlier applications to include equations now. Notice that we will translate a sentence into an equation.
- Step 1. Identify what you are asked to find and choose a variable to represent it.
- Step 2. Write a sentence that gives the information to find it.
- Step 3. Translate the sentence into an equation.
- Step 4. Solve the equation using good algebra techniques.
- Step 5. Check the answer in the problem and make sure it makes sense.
- Step 6. Write a complete sentence that answers the question.
Now that we have the strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we'll solve involve everyday situations, you can rely on your own experience.
Dezohn and his girlfriend enjoyed a dinner at a restaurant, and the bill was $68.50. They want to leave an 18% tip. If the tip will be 18% of the total bill, how much should the tip be?
Solution
| What are you asked to find? | the amount of the tip |
| Choose a variable to represent it. | Let t = amount of tip. |
| Write a sentence that give the information to find it. | The tip is 18% of the total bill. |
| Translate the sentence into an equation. | 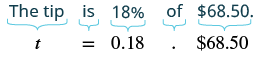 |
| Multiply. | t = 12.33 |
| Check. Is this answer reasonable? | If we approximate the bill to $70 and the percent to 20%, we would have a tip of $14. So a tip of $12.33 seems reasonable. |
| Write a complete sentence that answers the question. | The couple should leave a tip of $12.33. |
Cierra and her sister enjoyed a special dinner in a restaurant, and the bill was $81.50. If she wants to leave 18% of the total bill as her tip, how much should she leave?
- Answer
- $14.67
Kimngoc had lunch at her favorite restaurant. She wants to leave 15% of the total bill as her tip. If her bill was $14.40, how much will she leave for the tip?
- Answer
- $2.16
The label on Masao's breakfast cereal said that one serving of cereal provides 85 milligrams (mg) of potassium, which is 2% of the recommended daily amount. What is the total recommended daily amount of potassium?
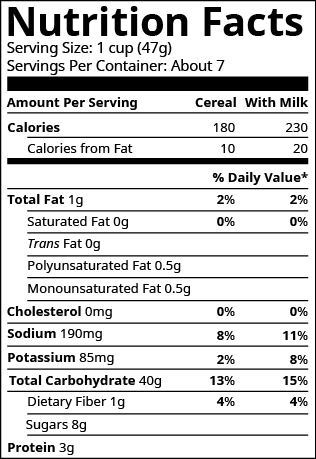
Solution
| What are you asked to find? | the total amount of potassium recommended |
| Choose a variable to represent it. | Let a = total amount of potassium. |
| Write a sentence that gives the information to find it. | 85 mg is 2% of the total amount. |
| Translate the sentence into an equation. |  |
| Divide both sides by 0.02. | $$\dfrac{85}{0.02} = \dfrac{0.02a}{0.02}$$ |
| Simplify. | 4,250 =a |
| Check: Is this answer reasonable? | Yes. 2% is a small percent and 85 is a small part of 4,250. |
| Write a complete sentence that answers the question. | The amount of potassium that is recommended is 4250 mg. |
One serving of wheat square cereal has 7 grams of fiber, which is 29% of the recommended daily amount. What is the total recommended daily amount of fiber?
- Answer
- 24.1 grams
One serving of rice cereal has 190 mg of sodium, which is 8% of the recommended daily amount. What is the total recommended daily amount of sodium?
- Answer
- 2,375 mg
Mitzi received some gourmet brownies as a gift. The wrapper said each brownie was 480 calories, and had 240 calories of fat. What percent of the total calories in each brownie comes from fat?
Solution
| What are you asked to find? | the percent of the total calories from fat |
| Choose a variable to represent it. | Let p = percent from fat. |
| Write a sentence that gives the information to find it. | What percent of 480 is 240? |
| Translate the sentence into an equation. |  |
| Divide both sides by 480. | $$\dfrac{p \cdot 480}{480} = \dfrac{240}{480}$$ |
| Simplify. | p = 0.5 |
| Convert to percent form. | p = 50% |
| Check. Is this answer reasonable? | Yes. 240 is half of 480, so 50% makes sense. |
| Write a complete sentence that answers the question. | Of the total calories in each brownie, 50% is fat. |
Veronica is planning to make muffins from a mix. The package says each muffin will be 230 calories and 60 calories will be from fat. What percent of the total calories is from fat? (Round to the nearest whole percent.)
- Answer
- 26%
The brownie mix Ricardo plans to use says that each brownie will be 190 calories, and 70 calories are from fat. What percent of the total calories are from fat?
- Answer
- 37%
Find Percent Increase and Percent Decrease
People in the media often talk about how much an amount has increased or decreased over a certain period of time. They usually express this increase or decrease as a percent.
To find the percent increase, first we find the amount of increase, which is the difference between the new amount and the original amount. Then we find what percent the amount of increase is of the original amount.
Step 1. Find the amount of increase.
- increase = new amount − original amount
Step 2. Find the percent increase as a percent of the original amount.
In 2011, the California governor proposed raising community college fees from $26 per unit to $36 per unit. Find the percent increase. (Round to the nearest tenth of a percent.)
Solution
| What are you asked to find? | the percent increase |
| Choose a variable to represent it. | Let p = percent. |
| Find the amount of increase. |  |
| Find the percent increase. | The increase is what percent of the original amount? |
| Translate to an equation. | 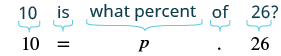 |
| Divide both sides by 26. | $$\dfrac{10}{26} = \dfrac{26p}{26}$$ |
| Round to the nearest thousandth. | 0.384 = p |
| Convert to percent form. | 38.4% = p |
| Write a complete sentence. | The new fees represent a 38.4% increase over the old fees. |
In 2011, the IRS increased the deductible mileage cost to 55.5 cents from 51 cents. Find the percent increase. (Round to the nearest tenth of a percent.)
- Answer
- 8.8%
In 1995, the standard bus fare in Chicago was $1.50. In 2008, the standard bus fare was $2.25. Find the percent increase. (Round to the nearest tenth of a percent.)
- Answer
- 50%
Finding the percent decrease is very similar to finding the percent increase, but now the amount of decrease is the difference between the original amount and the final amount. Then we find what percent the amount of decrease is of the original amount.
Step 1. Find the amount of decrease.
- decrease = original amount − new amount
Step 2. Find the percent decrease as a percent of the original amount.
The average price of a gallon of gas in one city in June 2014 was $3.71. The average price in that city in July was $3.64. Find the percent decrease.
Solution
The average price of a gallon of gas in one city in June 2014 was $3.71. The average price in that city in July was $3.64. Find the percent decrease.
| What are you asked to find? | the percent decrease |
| Choose a variable to represent it. | Let p = percent. |
| Find the amount of decrease. |  |
| Find the percent of decrease. | The decrease is what percent of the original amount? |
| Translate to an equation. | 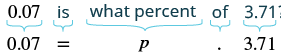 |
| Divide both sides by 3.71. | $$\dfrac{0.07}{3.71} = \dfrac{3.71p}{3.71}$$ |
| Round to the nearest thousandth. | 0.019 = p |
| Convert to percent form. | 1.9% = p |
| Write a complete sentence. | The price of gas decreased 1.9%. |
The population of one city was about 672,000 in 2010. The population of the city is projected to be about 630,000 in 2020. Find the percent decrease. (Round to the nearest tenth of a percent.)
- Answer
- 6.3%
Last year Sheila's salary was $42,000. Because of furlough days, this year her salary was $37,800. Find the percent decrease. (Round to the nearest tenth of a percent.)
- Answer
- 10%
Practice Makes Perfect
Translate and Solve Basic Percent Equations
In the following exercises, translate and solve.
- What number is 45% of 120?
- What number is 65% of 100?
- What number is 24% of 112?
- What number is 36% of 124?
- 250% of 65 is what number?
- 150% of 90 is what number?
- 800% of 2,250 is what number?
- 600% of 1,740 is what number?
- 28 is 25% of what number?
- 36 is 25% of what number?
- 81 is 75% of what number?
- 93 is 75% of what number?
- 8.2% of what number is $2.87?
- 6.4% of what number is $2.88?
- 11.5% of what number is $108.10?
- 12.3% of what number is $92.25?
- What percent of 260 is 78?
- What percent of 215 is 86?
- What percent of 1,500 is 540?
- What percent of 1,800 is 846?
- 30 is what percent of 20?
- 50 is what percent of 40?
- 840 is what percent of 480?
- 790 is what percent of 395?
Solve Applications of Percents
In the following exercises, solve the applications of percents.
- Geneva treated her parents to dinner at their favorite restaurant. The bill was $74.25. She wants to leave 16% of the total bill as a tip. How much should the tip be?
- When Hiro and his co-workers had lunch at a restaurant the bill was $90.50. They want to leave 18% of the total bill as a tip. How much should the tip be?
- Trong has 12% of each paycheck automatically deposited to his savings account. His last paycheck was $2,165. How much money was deposited to Trong's savings account?
- Cherise deposits 8% of each paycheck into her retirement account. Her last paycheck was $1,485. How much did Cherise deposit into her retirement account?
- One serving of oatmeal has 8 grams of fiber, which is 33% of the recommended daily amount. What is the total recommended daily amount of fiber?
- One serving of trail mix has 67 grams of carbohydrates, which is 22% of the recommended daily amount. What is the total recommended daily amount of carbohydrates?
- A bacon cheeseburger at a popular fast food restaurant contains 2,070 milligrams (mg) of sodium, which is 86% of the recommended daily amount. What is the total recommended daily amount of sodium?
- A grilled chicken salad at a popular fast food restaurant contains 650 milligrams (mg) of sodium, which is 27% of the recommended daily amount. What is the total recommended daily amount of sodium?
- The nutrition fact sheet at a fast food restaurant says the fish sandwich has 380 calories, and 171 calories are from fat. What percent of the total calories is from fat?
- The nutrition fact sheet at a fast food restaurant says a small portion of chicken nuggets has 190 calories, and 114 calories are from fat. What percent of the total calories is from fat?
- Emma gets paid $3,000 per month. She pays $750 a month for rent. What percent of her monthly pay goes to rent?
- Dimple gets paid $3,200 per month. She pays $960 a month for rent. What percent of her monthly pay goes to rent?
Find Percent Increase and Percent Decrease
In the following exercises, find the percent increase or percent decrease.
- Tamanika got a raise in her hourly pay, from $15.50 to $17.55. Find the percent increase.
- Ayodele got a raise in her hourly pay, from $24.50 to $25.48. Find the percent increase.
- Annual student fees at the University of California rose from about $4,000 in 2000 to about $9,000 in 2014. Find the percent increase.
- The price of a share of one stock rose from $12.50 to $50. Find the percent increase.
- According to Time magazine (7/19/2011) annual global seafood consumption rose from 22 pounds per person in 1960 to 38 pounds per person today. Find the percent increase. (Round to the nearest tenth of a percent.)
- In one month, the median home price in the Northeast rose from $225,400 to $241,500. Find the percent increase. (Round to the nearest tenth of a percent.)
- A grocery store reduced the price of a loaf of bread from $2.80 to $2.73. Find the percent decrease.
- The price of a share of one stock fell from $8.75 to $8.54. Find the percent decrease.
- Hernando's salary was $49,500 last year. This year his salary was cut to $44,055. Find the percent decrease.
- From 2000 to 2010, the population of Detroit fell from about 951,000 to about 714,000. Find the percent decrease. (Round to the nearest tenth of a percent.)
- In one month, the median home price in the West fell from $203,400 to $192,300. Find the percent decrease. (Round to the nearest tenth of a percent.)
- Sales of video games and consoles fell from $1,150 million to $1,030 million in one year. Find the percent decrease. (Round to the nearest tenth of a percent.)
Everyday Math
- Tipping At the campus coffee cart, a medium coffee costs $1.65. MaryAnne brings $2.00 with her when she buys a cup of coffee and leaves the change as a tip. What percent tip does she leave?
- Late Fees Alison was late paying her credit card bill of $249. She was charged a 5% late fee. What was the amount of the late fee?
Writing Exercises
- Without solving the problem “44 is 80% of what number”, think about what the solution might be. Should it be a number that is greater than 44 or less than 44? Explain your reasoning.
- Without solving the problem “What is 20% of 300?” think about what the solution might be. Should it be a number that is greater than 300 or less than 300? Explain your reasoning.
- After returning from vacation, Alex said he should have packed 50% fewer shorts and 200% more shirts. Explain what Alex meant.
- Because of road construction in one city, commuters were advised to plan their Monday morning commute to take 150% of their usual commuting time. Explain what this means.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) After reviewing this checklist, what will you do to become confident for all objectives?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


