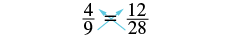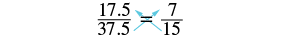6.5: Solve Proportions and their Applications (Part 1)
- Page ID
- 5030
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use the definition of proportion
- Solve proportions
- Solve applications using proportions
- Write percent equations as proportions
- Translate and solve percent proportions
Before you get started, take this readiness quiz.
- Simplify: \(\dfrac{\dfrac{1}{3}}{4}\). If you missed this problem, review Example 4.5.8.
- Solve: \(\dfrac{x}{4}\) = 20. If you missed this problem, review Example 4.12.5.
- Write as a rate: Sale rode his bike 24 miles in 2 hours. If you missed this problem, review Example 5.10.6.
Use the Definition of Proportion
In the section on Ratios and Rates we saw some ways they are used in our daily lives. When two ratios or rates are equal, the equation relating them is called a proportion.
A proportion is an equation of the form \(\dfrac{a}{b} = \dfrac{c}{d}\), where b ≠ 0, d ≠ 0.
The proportion states two ratios or rates are equal. The proportion is read “a is to b, as c is to d”.
The equation \(\dfrac{1}{2} = \dfrac{4}{8}\) is a proportion because the two fractions are equal. The proportion \(\dfrac{1}{2} = \dfrac{4}{8}\) is read “1 is to 2 as 4 is to 8”.
If we compare quantities with units, we have to be sure we are comparing them in the right order. For example, in the proportion \(\dfrac{20\; students}{1\; teacher} = \dfrac{60\; students}{3\; teachers}\) we compare the number of students to the number of teachers. We put students in the numerators and teachers in the denominators.
Write each sentence as a proportion: (a) 3 is to 7 as 15 is to 35. (b) 5 hits in 8 at bats is the same as 30 hits in 48 at-bats. (c) $1.50 for 6 ounces is equivalent to $2.25 for 9 ounces.
Solution
(a) 3 is to 7 as 15 is to 35
| Write as a proportion. | $$\dfrac{3}{7} = \dfrac{15}{35}$$ |
(b) 5 hits in 8 at bats is the same as 30 hits in 48 at-bats
| Write each fraction to compare hits to at-bats. | $$\dfrac{hits}{at-bats} = \dfrac{hits}{at-bats}$$ |
| Write as a proportion. | $$\dfrac{5}{8} = \dfrac{30}{48}$$ |
(c) $1.50 for 6 ounces is equivalent to $2.25 for 9 ounces
| Write each fraction to compare dollars to ounces. | $$\dfrac{\$}{ounces} = \dfrac{\$}{ounces}$$ |
| Write as a proportion. | $$\dfrac{1.50}{6} = \dfrac{2.25}{9}$$ |
Write each sentence as a proportion: (a) 5 is to 9 as 20 is to 36. (b) 7 hits in 11 at-bats is the same as 28 hits in 44 at-bats. (c) $2.50 for 8 ounces is equivalent to $3.75 for 12 ounces.
- Answer a
-
\(\frac{5}{9} = \frac{20}{36}\)
- Answer b
-
\(\frac{7}{11} = \frac{28}{44}\)
- Answer c
-
\(\frac{2.50}{8} = \frac{3.75}{12}\)
Write each sentence as a proportion: (a) 6 is to 7 as 36 is to 42. (b) 8 adults for 36 children is the same as 12 adults for 54 children. (c) $3.75 for 6 ounces is equivalent to $2.50 for 4 ounces.
- Answer a
-
\(\frac{6}{7} = \frac{36}{42}\)
- Answer b
-
\(\frac{8}{36} = \frac{12}{54}\)
- Answer c
-
\(\frac{3.75}{6} = \frac{2.50}{4}\)
Look at the proportions \(\dfrac{1}{2} = \dfrac{4}{8}\) and \(\dfrac{2}{3} = \dfrac{6}{9}\). From our work with equivalent fractions we know these equations are true. But how do we know if an equation is a proportion with equivalent fractions if it contains fractions with larger numbers? To determine if a proportion is true, we find the cross products of each proportion. To find the cross products, we multiply each denominator with the opposite numerator (diagonally across the equal sign). The results are called a cross products because of the cross formed. The cross products of a proportion are equal.

For any proportion of the form \(\dfrac{a}{b} = \dfrac{c}{d}\), where b ≠ 0, d ≠ 0, its cross products are equal.
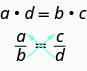
Cross products can be used to test whether a proportion is true. To test whether an equation makes a proportion, we find the cross products. If they are the equal, we have a proportion.
Determine whether each equation is a proportion: (a) \(\dfrac{4}{9} = \dfrac{12}{28}\) (b) \(\dfrac{17.5}{37.5} = \dfrac{7}{15}\)
Solution
To determine if the equation is a proportion, we find the cross products. If they are equal, the equation is a proportion.
(a) \(\dfrac{4}{9} = \dfrac{12}{28}\)
| Find the cross products. |
\[28 \cdot 4 = 112 \qquad 9 \cdot 12 = 108\] |
Since the cross products are not equal, 28 · 4 ≠ 9 · 12, the equation is not a proportion.
(b) \(\dfrac{17.5}{37.5} = \dfrac{7}{15}\)
| Find the cross products. |
\[15 \cdot 17.5 = 262.5 \qquad 37.5 \cdot 7 = 262.5\] |
Since the cross products are equal, 15 • 17.5 = 37.5 • 7, the equation is a proportion.
Determine whether each equation is a proportion: (a) \(\dfrac{7}{9} = \dfrac{54}{72}\) (b) \(\dfrac{24.5}{45.5} = \dfrac{7}{13}\)
- Answer a
-
no
- Answer b
-
yes
Determine whether each equation is a proportion: (a) \(\dfrac{8}{9} = \dfrac{56}{73}\) (b) \(\dfrac{28.5}{52.5} = \dfrac{8}{15}\)
- Answer a
-
no
- Answer b
-
no
Solve Proportions
To solve a proportion containing a variable, we remember that the proportion is an equation. All of the techniques we have used so far to solve equations still apply. In the next example, we will solve a proportion by multiplying by the Least Common Denominator (LCD) using the Multiplication Property of Equality.
Solve: \(\dfrac{x}{63} =\dfrac{4}{7}\).
Solution
| To isolate x, multiply both sides by the LCD, 63. | $$\textcolor{red}{63} \left(\dfrac{x}{63}\right) = \textcolor{red}{63} \left(\dfrac{4}{7}\right)$$ |
| Simplify. | $$x = \dfrac{9 \cdot \cancel{7} \cdot 4}{\cancel{7}}$$ |
| Divide the common factors. | $$x = 36$$ |
Check: To check our answer, we substitute into the original proportion.
| Substitute x = \(\textcolor{red}{36}\) | $$\dfrac{\textcolor{red}{36}}{63} \stackrel{?}{=} \dfrac{4}{7}$$ |
| Show common factors. | $$\dfrac{4 \cdot 9}{7 \cdot 9} \stackrel{?}{=} \dfrac{4}{7}$$ |
| Simplify. | $$\dfrac{4}{7} = \dfrac{4}{7} \; \checkmark$$ |
Solve the proportion: \(\dfrac{n}{84} = \dfrac{11}{12}\).
- Answer
-
77
Solve the proportion: \(\dfrac{y}{96} = \dfrac{13}{12}\).
- Answer
-
104
When the variable is in a denominator, we’ll use the fact that the cross products of a proportion are equal to solve the proportions.
We can find the cross products of the proportion and then set them equal. Then we solve the resulting equation using our familiar techniques.
Solve: \(\dfrac{144}{a} =\dfrac{9}{4}\).
Solution
Notice that the variable is in the denominator, so we will solve by finding the cross products and setting them equal.
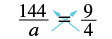
| Find the cross products and set them equal. | 4 • 144 = a • 9 |
| Simplify. | 576 = 9a |
| Divide both sides by 9. | $$\dfrac{576}{9} = \dfrac{9a}{9}$$ |
| Simplify. | $$64 = a$$ |
Check your answer.
| Substitute a = \(\textcolor{red}{64}\) | $$\dfrac{144}{\textcolor{red}{64}} \stackrel{?}{=} \dfrac{9}{4}$$ |
| Show common factors. | $$\dfrac{9 \cdot 16}{4 \cdot 16} \stackrel{?}{=} \dfrac{9}{4}$$ |
| Simplify. | $$\dfrac{9}{4} = \dfrac{9}{4} \; \checkmark$$ |
Another method to solve this would be to multiply both sides by the LCD, 4a. Try it and verify that you get the same solution.
Solve the proportion: \(\dfrac{91}{b} = \dfrac{7}{5}\).
- Answer
-
65
Solve the proportion: \(\dfrac{39}{c} = \dfrac{13}{8}\).
- Answer
-
24
Solve: \(\dfrac{52}{91} = \dfrac{-4}{y}\)
Solution
| Find the cross products and set them equal. | 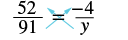 |
| y • 52 = 91(-4) | |
| Simplify. | 52y = -364 |
| Divide both sides by 52. | $$\dfrac{52y}{52} = \dfrac{-364}{52}$$ |
| Simplify. | $$y = -7$$ |
Check:
| Substitute y = \(\textcolor{red}{-7}\) | $$\dfrac{52}{91} \stackrel{?}{=} \dfrac{-4}{\textcolor{red}{-7}}$$ |
| Show common factors. | $$\dfrac{13 \cdot 4}{13 \cdot 7} \stackrel{?}{=} \dfrac{-4}{\textcolor{red}{-7}}$$ |
| Simplify. | $$\dfrac{4}{7} = \dfrac{4}{7} \; \checkmark$$ |
Solve the proportion: \(\dfrac{84}{98} = \dfrac{-6}{x}\).
- Answer
-
-7
Solve the proportion: \(\dfrac{-7}{y} = \dfrac{105}{135}\).
- Answer
-
-9
Solve Applications Using Proportions
The strategy for solving applications that we have used earlier in this chapter, also works for proportions, since proportions are equations. When we set up the proportion, we must make sure the units are correct—the units in the numerators match and the units in the denominators match.
When pediatricians prescribe acetaminophen to children, they prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of the child’s weight. If Zoe weighs 80 pounds, how many milliliters of acetaminophen will her doctor prescribe?
Solution
| Identify what you are asked to find. | How many ml of acetaminophen the doctor will prescribe? |
| Choose a variable to represent it. | Let a = ml of acetaminophen. |
| Write a sentence that gives the information to find it. | If 5 ml is prescribed for every 25 pounds, how much will be prescribed for 80 pounds? |
| Translate into a proportion. | $$\dfrac{ml}{pounds} = \dfrac{ml}{pounds} \tag{6.5.24}$$ |
| Substitute given values—be careful of the units. | $$\dfrac{5}{25} = \dfrac{a}{80} \tag{6.5.25}$$ |
| Multiply both sides by 80. | $$80 \cdot \dfrac{5}{25} = 80 \cdot \dfrac{a}{80} \tag{6.5.26}$$ |
| Multiply and show common factors. | $$\dfrac{16 \cdot 5 \cdot 5}{5 \cdot 5} = \dfrac{80a}{80} \tag{6.5.27}$$ |
| Simplify. | $$16 = a \tag{6.5.28}$$ |
| Check if the answer is reasonable. | Yes. Since 80 is about 3 times 25, the medicine should be about 3 times 5. |
| Write a complete sentence. | The pediatrician would prescribe 16 ml of acetaminophen to Zoe. |
You could also solve this proportion by setting the cross products equal.
Pediatricians prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Emilia, who weighs 60 pounds?
- Answer
-
12 ml
For every 1 kilogram (kg) of a child’s weight, pediatricians prescribe 15 milligrams (mg) of a fever reducer. If Isabella weighs 12 kg, how many milligrams of the fever reducer will the pediatrician prescribe?
- Answer
-
180 mg
One brand of microwave popcorn has 120 calories per serving. A whole bag of this popcorn has 3.5 servings. How many calories are in a whole bag of this microwave popcorn?
Solution
| Identify what you are asked to find. | How many calories are in a whole bag of microwave popcorn? |
| Choose a variable to represent it. | Let c = number of calories. |
| Write a sentence that gives the information to find it. | If there are 120 calories per serving, how many calories are in a whole bag with 3.5 servings? |
| Translate into a proportion. | $$\dfrac{calories}{serving} = \dfrac{calories}{serving} \tag{6.5.29}$$ |
| Substitute given values. | $$\dfrac{120}{1} = \dfrac{c}{3.5} \tag{6.5.30}$$ |
| Multiply both sides by 3.5. | $$(3.5) \left(\dfrac{120}{1}\right) = (3.5) \left(\dfrac{c}{3.5}\right) \tag{6.5.31}$$ |
| Multiply. | $$420 = c \tag{6.5.32}$$ |
| Check if the answer is reasonable. | Yes. Since 3.5 is between 3 and 4, the total calories should be between 360 (3 • 120) and 480 (4 • 120). |
| Write a complete sentence. | The whole bag of microwave popcorn has 420 calories. |
Marissa loves the Caramel Macchiato at the coffee shop. The 16 oz. medium size has 240 calories. How many calories will she get if she drinks the large 20 oz. size?
- Answer
-
300
Yaneli loves Starburst candies, but wants to keep her snacks to 100 calories. If the candies have 160 calories for 8 pieces, how many pieces can she have in her snack?
- Answer
-
5
Josiah went to Mexico for spring break and changed $325 dollars into Mexican pesos. At that time, the exchange rate had $1 U.S. is equal to 12.54 Mexican pesos. How many Mexican pesos did he get for his trip?
Solution
| Identify what you are asked to find. | How many Mexican pesos did Josiah get? |
| Choose a variable to represent it. | Let p = number of pesos. |
| Write a sentence that gives the information to find it. | If $1 U.S. is equal to 12.54 Mexican pesos, then $325 is how many pesos? |
| Translate into a proportion. | $$\dfrac{\$}{pesos} = \dfrac{\$}{pesos} \tag{6.5.33}$$ |
| Substitute given values. | $$\dfrac{1}{12.54} = \dfrac{325}{p} \tag{6.5.34}$$ |
| The variable is in the denominator, so find the cross products and set them equal. | $$p \cdot 1 = 12.54 (325) \tag{6.5.35}$$ |
| Simplify. | $$c = 4,075.5 \tag{6.5.36}$$ |
| Check if the answer is reasonable. | Yes, $100 would be $1,254 pesos. $325 is a little more than 3 times this amount. |
| Write a complete sentence. | Josiah has 4075.5 pesos for his spring break trip. |
Yurianna is going to Europe and wants to change $800 dollars into Euros. At the current exchange rate, $1 US is equal to 0.738 Euro. How many Euros will she have for her trip?
- Answer
-
590 Euros
Corey and Nicole are traveling to Japan and need to exchange $600 into Japanese yen. If each dollar is 94.1 yen, how many yen will they get?
- Answer
-
56,460 yen
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."