11.R: Sequences, Probability and Counting Theory (Review)
( \newcommand{\kernel}{\mathrm{null}\,}\)
11.1 Sequences and Their Notations
1) Write the first four terms of the sequence defined by the recursive formula a1=2,an=an−1+n.
- Answer
-
2,4,7,11
2) Evaluate 6!(5−3)!3!.
3) Write the first four terms of the sequence defined by the explicit formula an=10n+3.
- Answer
-
13,103,1003,10003
4) Write the first four terms of the sequence defined by the explicit formula an=n!n(n+1)!.
11.2 Arithmetic Sequences
1) Is the sequence 47,4721,8221,397,… arithmetic? If so, find the common difference.
- Answer
-
The sequence is arithmetic. The common difference is d=53.
2) Is the sequence 2,4,8,16,… arithmetic? If so, find the common difference.
3) An arithmetic sequence has the first term a1=18 and common difference d=8. What are the first five terms?
- Answer
-
18,10,2,−6,−14
4) An arithmetic sequence has terms a3=11.7 and a8=−14.6. What is the first term?
5) Write a recursive formula for the arithmetic sequence −20,−10,0,10,…
- Answer
-
a1=−20,an=an−1+10
6) Write a recursive formula for the arithmetic sequence 0,−12,−1,−32,…, and then find the 31st term.
7) Write an explicit formula for the arithmetic sequence 78,2924,3724,158,…
- Answer
-
an=13n+1324
8) How many terms are in the finite arithmetic sequence 12,20,28,…,172?
11.3 Geometric Sequences
1) Find the common ratio for the geometric sequence 2.5,5,10,20,…
- Answer
-
r=2
2) Is the sequence 4,16,28,40,… geometric? If so find the common ratio. If not, explain why.
3) A geometric sequence has terms a7=16,384 and a9=262,144. What are the first five terms?
- Answer
-
4,16,64,256,1024
4) A geometric sequence has the first term a1=−3 and common ratio r=12. What is the 8th term?
5) What are the first five terms of the geometric sequence a1=3,an=4⋅an−1?
- Answer
-
3,12,48,192,768
6) Write a recursive formula for the geometric sequence 1,13,19,127,…
7) Write an explicit formula for the geometric sequence −15,−115,−145,−1135,…
- Answer
-
an=−15⋅(13)n−1
8) How many terms are in the finite geometric sequence −5,−53,−59,…,−559,049?
11.4 Series and Their Notations
1) Use summation notation to write the sum of terms 12m+5 from m=0 to m=5.
- Answer
-
5∑m=0(12m+5)
2) Use summation notation to write the sum that results from adding the number 13 twenty times.
3) Use the formula for the sum of the first n terms of an arithmetic series to find the sum of the first eleven terms of the arithmetic series 2.5,4,5.5,…
- Answer
-
S11=110
4) A ladder has 15 tapered rungs, the lengths of which increase by a common difference. The first rung is 5 inches long, and the last rung is 20 inches long. What is the sum of the lengths of the rungs?
5) Use the formula for the sum of the first n terms of a geometric series to find S9 for the series 12,6,3,32,…
- Answer
-
S9≈23.95
6) The fees for the first three years of a hunting club membership are given in the Table below. If fees continue to rise at the same rate, how much will the total cost be for the first ten years of membership?
| Year | Membership Fees |
|---|---|
| 1 | $1500 |
| 2 | $1950 |
| 3 | $2535 |
7) Find the sum of the infinite geometric series ∑∞k=145⋅(−13)k−1.
- Answer
-
S=1354
8) A ball has a bounce-back ratio of 35 the height of the previous bounce. Write a series representing the total distance traveled by the ball, assuming it was initially dropped from a height of 5 feet. What is the total distance? (Hint: the total distance the ball travels on each bounce is the sum of the heights of the rise and the fall.)
9) Alejandro deposits $80 of his monthly earnings into an annuity that earns 6.25% annual interest, compounded monthly. How much money will he have saved after 5 years?
- Answer
-
$5,617.61
10) The twins Sarah and Scott both opened retirement accounts on their 21st birthday. Sarah deposits $4,800.00 each year, earning 5.5% annual interest, compounded monthly. Scott deposits $3,600.00 each year, earning 8.5% annual interest, compounded monthly. Which twin will earn the most interest by the time they are 55 years old? How much more?
11.5 Counting Principles
1) How many ways are there to choose a number from the set {−10,−6,4,10,12,18,24,32} that is divisible by either 4 or 6?
- Answer
-
6
2) In a group of 20 musicians, 12 play piano, 7 play trumpet, and 2 play both piano and trumpet. How many musicians play either piano or trumpet?
3) How many ways are there to construct a 4-digit code if numbers can be repeated?
- Answer
-
104=10,000
4) A palette of water color paints has 3 shades of green, 3 shades of blue, 2 shades of red, 2 shades of yellow, and 1 shade of black. How many ways are there to choose one shade of each color?
5) Calculate P(18,4).
- Answer
-
P(18,4)=73,440
6) In a group of 5 freshman, 10 sophomores, 3 juniors, and 2 seniors, how many ways can a president, vice president, and treasurer be elected?
7) Calculate C(15,6).
- Answer
-
C(15,6)=5005
8) A coffee shop has 7 Guatemalan roasts, 4 Cuban roasts, and 10 Costa Rican roasts. How many ways can the shop choose 2 Guatemalan, 2 Cuban, and 3 Costa Rican roasts for a coffee tasting event?
9) How many subsets does the set {1,3,5,…,99} have?
- Answer
-
250=1.13×1015
10) A day spa charges a basic day rate that includes use of a sauna, pool, and showers. For an extra charge, guests can choose from the following additional services: massage, body scrub, manicure, pedicure, facial, and straight-razor shave. How many ways are there to order additional services at the day spa?
11) How many distinct ways can the word DEADWOOD be arranged?
- Answer
-
8!3!2!=3360
12) How many distinct rearrangements of the letters of the word DEADWOOD are there if the arrangement must begin and end with the letter D?
11.6 Binomial Theorem
1) Evaluate the binomial coefficient (238).
- Answer
-
490,314
2) Use the Binomial Theorem to expand (3x+12y)6.
3) Use the Binomial Theorem to write the first three terms of (2a+b)17.
- Answer
-
131,072a17+1,114,112a16b+4,456,448a15b2
4) Find the fourth term of (3a2−2b)11 without fully expanding the binomial.
11.7 Probability
For the exercises 1-7, assume two die are rolled.
1) Construct a table showing the sample space.
- Answer
-
1 2 3 4 5 6 1 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 2 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 3 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 4 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 5 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 6 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6
2) What is the probability that a roll includes a 2?
3) What is the probability of rolling a pair?
- Answer
-
16
4) What is the probability that a roll includes a 2 or results in a pair?
5) What is the probability that a roll doesn’t include a 2 or result in a pair?
- Answer
-
59
6) What is the probability of rolling a 5 or a 6?
7) What is the probability that a roll includes neither a 5 nor a 6?
- Answer
-
49
For the exercises 8-11, use the following data: An elementary school survey found that 350 of the 500 students preferred soda to milk. Suppose 8 children from the school are attending a birthday party. (Show calculations and round to the nearest tenth of a percent.)
8) What is the percent chance that all the children attending the party prefer soda?
9) What is the percent chance that at least one of the children attending the party prefers milk?
- Answer
-
1−C(350,8)C(500,8)≈94.4%
10) What is the percent chance that exactly 3 of the children attending the party prefer soda?
11) What is the percent chance that exactly 3 of the children attending the party prefer milk?
- Answer
-
C(150,3)C(350,5)C(500,8)≈25.6%
Practice Test
1) Write the first four terms of the sequence defined by the recursive formula a=−14,an=2+an−12
- Answer
-
−14,−6,−2,0
2) Write the first four terms of the sequence defined by the explicit formula an=n2−n−1n!.
3) Is the sequence 0.3,1.2,2.1,3,… arithmetic? If so find the common difference.
- Answer
-
The sequence is arithmetic. The common difference is d=0.9.
4) An arithmetic sequence has the first term a1=−4 and common difference d=−43. What is the 6th term?
5) Write a recursive formula for the arithmetic sequence −2,−72,−5,−132,… and then find the 22nd term.
- Answer
-
a1=−2,an=an−1−32;a22=−672
6) Write an explicit formula for the arithmetic sequence 15.6,15,14.4,13.8,… and then find the 32nd term.
7) Is the sequence −2,−1,−12,−14,… geometric? If so find the common ratio. If not, explain why.
- Answer
-
The sequence is geometric. The common ratio is r=12.
8) What is the 11th term of the geometric sequence −1.5,−3,−6,−12,…?
9) Write a recursive formula for the geometric sequence 1,−12,14,−18,…
- Answer
-
a1=1,an=−12⋅an−1
10) Write an explicit formula for the geometric sequence 4,−43,49,−427,…
11) Use summation notation to write the sum of terms 3k2−56k from k=−3 to k=15.
- Answer
-
15∑k=−3(3k2−56k)
12) A community baseball stadium has 10 seats in the first row, 13 seats in the second row, 16 seats in the third row, and so on. There are 56 rows in all. What is the seating capacity of the stadium?
13) Use the formula for the sum of the first n terms of a geometric series to find 7∑k=1−0.2⋅(−5)k−1
- Answer
-
S7=−2604.2
14) Find the sum of the infinite geometric series ∞∑k=113⋅(−15)k−1
15) Rachael deposits $3,600 into a retirement fund each year. The fund earns 7.5% annual interest, compounded monthly. If she opened her account when she was 20 years old, how much will she have by the time she’s 55? How much of that amount was interest earned?
- Answer
-
Total in account: $140,355.75 Interest earned: $14,355.75
16) In a competition of 50 professional ballroom dancers, 22 compete in the fox-trot competition, 18 compete in the tango competition, and 6 compete in both the fox-trot and tango competitions. How many dancers compete in the fox-trot or tango competitions?
17) A buyer of a new sedan can custom order the car by choosing from 5 different exterior colors, 3 different interior colors, 2 sound systems, 3 motor designs, and either manual or automatic transmission. How many choices does the buyer have?
- Answer
-
5×3×2×3×2=180
18) To allocate annual bonuses, a manager must choose his top four employees and rank them first to fourth. In how many ways can he create the “Top-Four” list out of the 32 employees?
19) A rock group needs to choose 3 songs to play at the annual Battle of the Bands. How many ways can they choose their set if have 15 songs to pick from?
- Answer
-
C(15,3)=455
20) A self-serve frozen yogurt shop has 8 candy toppings and 4 fruit toppings to choose from. How many ways are there to top a frozen yogurt?
21) How many distinct ways can the word EVANESCENCE be arranged if the anagram must end with the letter E?
- Answer
-
10!2!3!2!=151,200
22) Use the Binomial Theorem to expand (32x−12y)5.
23) Find the seventh term of (x2−12)13 without fully expanding the binomial.
- Answer
-
429x1416
For the exercises 24-28, use the spinner in the Figure below.
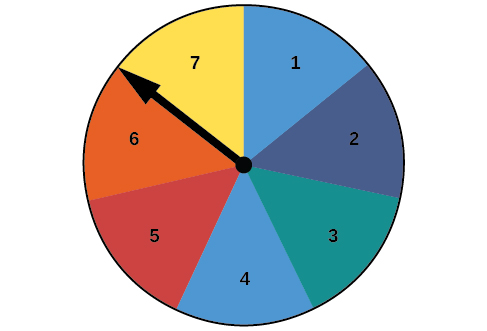
24) Construct a probability model showing each possible outcome and its associated probability. (Use the first letter for colors.)
25) What is the probability of landing on an odd number?
- Answer
-
47
26) What is the probability of landing on blue?
27) What is the probability of landing on blue or an odd number?
- Answer
-
57
28) What is the probability of landing on anything other than blue or an odd number?
29) A bowl of candy holds 16 peppermint, 14 butterscotch, and 10 strawberry flavored candies. Suppose a person grabs a handful of 7 candies. What is the percent chance that exactly 3 are butterscotch? (Show calculations and round to the nearest tenth of a percent.)
- Answer
-
C(14,3)C(26,4)C(40,7)≈29.2%
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


