1.2: Domain and Range
( \newcommand{\kernel}{\mathrm{null}\,}\)
One of our main goals in mathematics is to model the real world with mathematical functions. In doing so, it is important to keep in mind the limitations of those models we create.
This table shows a relationship between circumference and height of a tree as it grows.
| Circumference, c | 1.7 | 2.5 | 5.5 | 8.2 | 13.7 |
| Height, h | 24.5 | 31 | 45.2 | 54.6 | 92.1 |
While there is a strong relationship between the two, it would certainly be ridiculous to talk about a tree with a circumference of -3 feet, or a height of 3000 feet. When we identify limitations on the inputs and outputs of a function, we are determining the domain and range of the function.
Definitions: Domain and Range
- Domain: The set of possible input values to a function
- Range: The set of possible output values of a function
Example 1.2.1
Using the tree table above, determine a reasonable domain and range.
Solution
We could combine the data provided with our own experiences and reason to approximate the domain and range of the function h=f(c). For the domain, possible values for the input circumference c, it doesn’t make sense to have negative values, so c>0. We could make an educated guess at a maximum reasonable value, or look up that the maximum circumference measured is about 119 feet. With this information, we would say a reasonable domain is 0<c≤119 feet.
Similarly for the range, it doesn’t make sense to have negative heights, and the maximum height of a tree could be looked up to be 379 feet, so a reasonable range is 0<h≤379 feet.
Example 1.2.2
When sending a letter through the United States Postal Service, the price depends upon the weight of the letter (https://pe.usps.com/text/dmm300/Notice123.htm, retrieved August 6, 2018), as shown in the table below. Determine the domain and range.
|
Weight not Over |
Price |
|---|---|
|
1 ounce |
$0.50 |
|
2 ounces |
$0.71 |
|
3 ounces |
$0.92 |
|
3.5 ounces |
$1.13 |
Suppose we notate Weight by w and Price by p, and set up a function named P, where Price, p is a function of Weight, w.p=P(w).
Since acceptable weights are 3.5 ounces or less, and negative weights don’t make sense, the domain would be 0<w≤3.5. Technically 0 could be included in the domain, but logically it would mean we are mailing nothing, so it doesn’t hurt to leave it out.
Since possible prices are from a limited set of values, we can only define the range of this function by listing the possible values. The range is p = $0.50, $0.71, $0.92, or $1.13.
Try it now
The population of a small town in the year 1960 was 100 people. Since then the population has grown to 1400 people reported during the 2010 census. Choose descriptive variables for your input and output and use interval notation to write the domain and range.
- Answer
-
Domain; y= years [1960, 2010]
Range, p= population, [100, 1400]
Notation
In the previous examples, we used inequalities to describe the domain and range of the functions. This is one way to describe intervals of input and output values, but is not the only way. Let us take a moment to discuss notation for domain and range.
Using inequalities, such as 0<c≤163, 0<w≤3.5, and 0<h≤379 imply that we are interested in all values between the low and high values, including the high values in these examples.
However, occasionally we are interested in a specific list of numbers like the range for the price to send letters, p = $0.44, $0.61, $0.78, or $0.95. These numbers represent a set of specific values: {0.44, 0.61, 0.78, 0.95}
Representing values as a set, or giving instructions on how a set is built, leads us to another type of notation to describe the domain and range.
Suppose we want to describe the values for a variable x that are 10 or greater, but less than 30. In inequalities, we would write 10≤x<30.
When describing domains and ranges, we sometimes extend this into set-builder notation, which would look like this: {x | 10≤x<30}. The curly brackets {} are read as “the set of”, and the vertical bar is read as “such that”, so altogether we would read {x | 10≤x<30} as “the set of x-values such that 10 is less than or equal to x and x is less than 30.”
When describing ranges in set-builder notation, we could similarly write something like {f(x) | 0<f(x)<30}, or if the output had its own variable, we could use it. So for our tree height example above, we could write for the range {h | 0<h≤379}. In set-builder notation, if a domain or range is not limited, we could write {t | t is a real number}, or {t | t∈R}, read as “the set of t-values such that t is an element of the set of real numbers.
A more compact alternative to set-builder notation is interval notation, in which intervals of values are referred to by the starting and ending values. Curved parentheses are used for “strictly less than,” and square brackets are used for “less than or equal to.” Since infinity is not a number, we can’t include it in the interval, so we always use curved parentheses with ∞ and - ∞. The table below will help you see how inequalities correspond to set-builder notation and interval notation:
| Inequality | Set Builder Notation | Interval notation |
|---|---|---|
| 5<h≤10 | {h | 5<h≤10} | (5, 10] |
| 5≤h<10 | {h | 5≤h<10} | [5, 10) |
| 5<h<10 | {h | 5<h<10} | (5, 10) |
| h<10 | {h | h<10} | (−∞,10) |
| h≥10 | {h | h≥10} | [10,∞) |
| all real numbers | {h | h∈R} | (−∞,∞) |
To combine two intervals together, using inequalities or set-builder notation we can use the word “or”. In interval notation, we use the union symbol, ∪, to combine two unconnected intervals together.
Example 1.2.3
Describe the intervals of values shown on the line graph below using set builder and interval notations.

To describe the values, x, that lie in the intervals shown above we would say, “x is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.”
- As an inequality it is: 1≤x≤3orx>5
- In set builder notation: {x|1≤x≤3orx>5}
- In interval notation: [1,3]∪(5,∞)
Remember when writing or reading interval notation:
Using a square bracket [ means the start value is included in the set
Using a parenthesis ( means the start value is not included in the set
Try it now
Given the following interval, write its meaning in words, set builder notation, and interval notation.

- Answer
-
a. Values that are less than or equal to -2, or values that are greater than or equal to -1 and less than 3
b. {x | x≤−2 or −1≤x<3}
c. (−∞,−2]∪[−1,3)
Domain and Range from Graphs
We can also talk about domain and range based on graphs. Since domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the graph. Remember that input values are almost always shown along the horizontal axis of the graph. Likewise, since range is the set of possible output values, the range of a graph we can see from the possible values along the vertical axis of the graph.
Be careful – if the graph continues beyond the window on which we can see the graph, the domain and range might be larger than the values we can see.
Example 1.2.4
Determine the domain and range of the graph below.
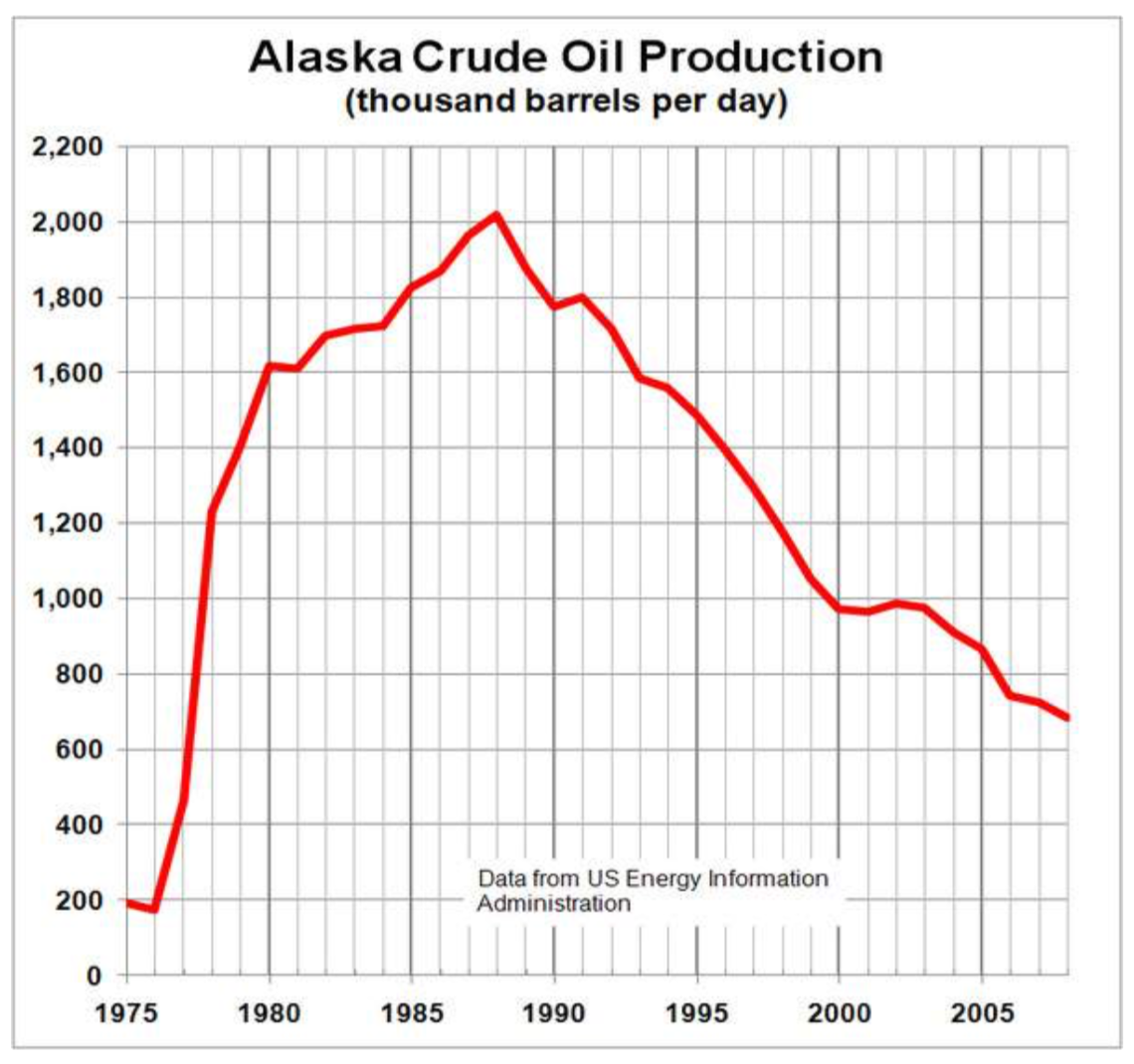
Solution
In the graph above (http://commons.wikimedia.org/wiki/Fi...Production.PNG, CC-BY-SA, July 19, 2010), the input quantity along the horizontal axis appears to be “year”, which we could notate with the variable y. The output is “thousands of barrels of oil per day”, which we might notate with the variable b, for barrels. The graph would likely continue to the left and right beyond what is shown, but based on the portion of the graph that is shown to us, we can determine the domain is 1975≤y≤2008, and the range is approximately 180≤b≤2010.
In interval notation, the domain would be [1975, 2008] and the range would be about [180, 2010]. For the range, we have to approximate the smallest and largest outputs since they don’t fall exactly on the grid lines.
Remember that, as in the previous example, x and y are not always the input and output variables. Using descriptive variables is an important tool to remembering the context of the problem.
Try it now
Given the graph below write the domain and range in interval notation
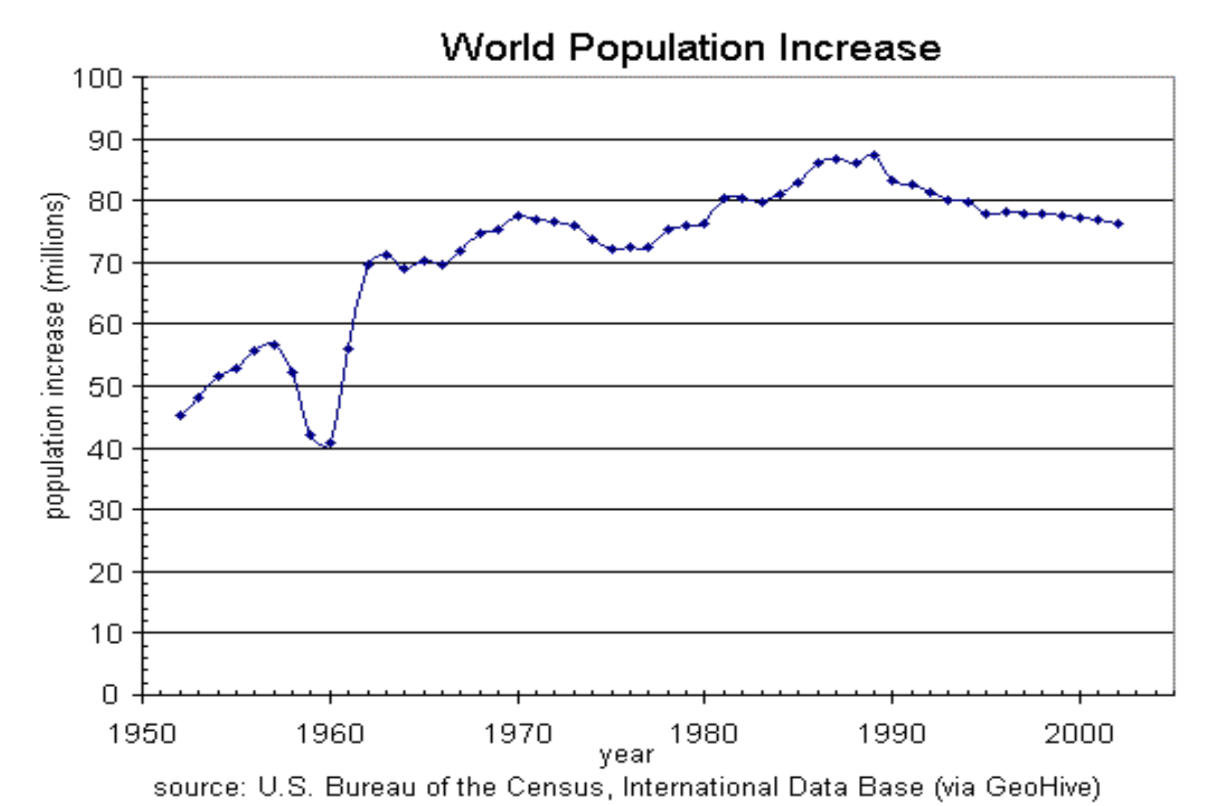
- Answer
-
Domain; y= years, [1952, 2002]; Range, p= population in millions, [40, 88]
Domains and Ranges of the Toolkit Functions
We will now return to our set of toolkit functions to note the domain and range of each.
Constant Function: f(x)=c
- The domain here is not restricted; x can be anything. When this is the case we say the domain is all real numbers. The outputs are limited to the constant value of the function.
- Domain: (−∞,∞)
- Range: [c]
- Since there is only one output value, we list it by itself in square brackets.
Identity Function: f(x)=x
- Domain: (−∞,∞)
- Range: (−∞,∞)
Quadratic Function: f(x)=x2
- Domain: (−∞,∞)
- Range: [0,∞)
- Multiplying a negative or positive number by itself can only yield a positive output.
Cubic Function: f(x)=x3
- Domain: (−∞,∞)
- Range: (−∞,∞)
Reciprocal: f(x)=1x
- Domain: (−∞,0)∪(0,∞)
- Range: (−∞,0)∪(0,∞)
- We cannot divide by 0 so we must exclude 0 from the domain.
- One divide by any value can never be 0, so the range will not include 0.
Reciprocal Squared: f(x)=1x2
- Domain: (−∞,0)∪(0,∞)
- Range: (0,∞)
- We cannot divide by 0 so we must exclude 0 from the domain.
Cube Root: f(x)=3√x
- Domain: (−∞,∞)
- Range: (−∞,∞)
Square Root: f(x)=2√x, commonly just written as, f(x)=√x
- Domain: [0,∞)
- Range: [0,∞)
- When dealing with the set of real numbers we cannot take the square root of a negative number so the domain is limited to 0 or greater.
Absolute Value Function: f(x)=|x|
- Domain: (−∞,∞)
- Range: [0,∞)
- Since absolute value is defined as a distance from 0, the output can only be greater than or equal to 0.
Example 1.2.5
Find the domain of each function:
- f(x)=2√x+4
- g(x)=36−3x
Solution
a) Since we cannot take the square root of a negative number, we need the inside of the square root to be non-negative.
x+4≥0 when x≥−4.
The domain of f(x) is [−4,∞).
b) We cannot divide by zero, so we need the denominator to be non-zero.
6−3x=0 when x = 2, so we must exclude 2 from the domain.
The domain of g(x) is (−∞,2)∪(2,∞).
Piecewise Functions
In the toolkit functions we introduced the absolute value function f(x)=|x|.
With a domain of all real numbers and a range of values greater than or equal to 0, the absolute value can be defined as the magnitude or modulus of a number, a real number value regardless of sign, the size of the number, or the distance from 0 on the number line. All of these definitions require the output to be greater than or equal to 0.
If we input 0, or a positive value the output is unchanged
f(x)=x if x≥0
If we input a negative value the sign must change from negative to positive.
f(x)=−x if x<0, since multiplying a negative value by -1 makes it positive.
Since this requires two different processes or pieces, the absolute value function is often called the most basic piecewise defined function.
Definition: Piecewise Function
A piecewise function is a function in which the formula used depends upon the domain the input lies in. We notate this idea like:
f(x)={formula 1 if domain to use formula 1formula 2 if domain to use formula 2formula 3 if domain to use formula 3
Example 1.2.6
A museum charges $5 per person for a guided tour with a group of 1 to 9 people, or a fixed $50 fee for 10 or more people in the group. Set up a function relating the number of people, n, to the cost, C.
Solution
To set up this function, two different formulas would be needed. C = 5n would work for n values under 10, and C = 50 would work for values of n ten or greater. Notating this:
C(n)={5nif0<n<1050ifn≥10
Example 1.2.7
A cell phone company uses the function below to determine the cost, C, in dollars for g gigabytes of data transfer.
C(g)={25if0<g<225+10(g−2)ifg≥2
Find the cost of using 1.5 gigabytes of data, and the cost of using 4 gigabytes of data.
Solution
To find the cost of using 1.5 gigabytes of data, C(1.5), we first look to see which piece of domain our input falls in. Since 1.5 is less than 2, we use the first formula, giving C(1.5) = $25.
The find the cost of using 4 gigabytes of data, C(4), we see that our input of 4 is greater than 2, so we’ll use the second formula. C(4) = 25 + 10(4 - 2) = $45.
Example 1.2.8
Sketch a graph of the function f(x)={x2ifx≤13if1<x≤26−xifx>2
Solution
The first two component functions are from our library of Toolkit functions, so we know their shapes. We can imagine graphing each function, then limiting the graph to the indicated domain. At the endpoints of the domain, we put open circles to indicate where the endpoint is not included, due to a strictly-less-than inequality, and a closed circle where the endpoint is included, due to a less-than-or-equal-to inequality.
For the third function, you should recognize this as a linear equation from your previous coursework. If you remember how to graph a line using slope and intercept, you can do that. Otherwise, we could calculate a couple values, plot points, and connect them with a line.
- At x=2, f(2)=6−2=4. We place an open circle here.
- At x=3, f(3)=6−3=3. Connect these points with a line.
Now that we have each piece individually, we combine them onto the same graph:
Try It Now
At Pierce College during the 2009-2010 school year tuition rates for in-state residents were $89.50 per credit for the first 10 credits, $33 per credit for credits 11-18, and for over 18 credits the rate is $73 per credit (www.pierce.ctc.edu/dist/tuit...ition_rate.pdf, retrieved August 6, 2010). Write a piecewise defined function for the total tuition, T, at Pierce College during 2009-2010 as a function of the number of credits taken, c. Be sure to consider a reasonable domain and range
- Answer
-
T(c)={89.5cifc≤10895+33(c−10)if10<c≤181159+73(c−18)ifc>18 Tuition, T, as a function of credits, c.
Reasonable domain should be whole numbers 0 to (answers may vary), e.g. [0, 23]
Reasonable range should be $0 – (answers may vary), e.g. [0,1524]
Important Topics of this Section
- Definition of domain
- Definition of range
- Inequalities
- Interval notation
- Set builder notation
- Domain and Range from graphs
- Domain and Range of toolkit functions
- Piecewise defined functions


