2.2: Introduction to functions
- Page ID
- 48955
We now formally introduce the notion of a function. A first example was provided by a straight line such as, for example, \(y=5x+4\). Note, that for each given \(x\) we obtain an induced \(y\). (For example, for \(x=3\), we obtain \(y=5\cdot 3+4=19\).)
A function \(f\) consists of two sets, a set \(D\) of inputs called the domain and a set \(C\) of possible outputs called the codomain, and an assignment that assigns to each input \(x\) exactly one output \(y\).
A function \(f\) with domain \(D\) and codomain \(C\) is denoted by
\[f:D\to C \nonumber \]
If \(x\) is in the domain \(D\) (an input), then we denote by \(f(x)=y\) the output that is assigned by \(f\) to \(x\).
Sometimes it is of interest to know the set of all elements in the codomain that actually occur as an output. This set is a subset of the codomain and is called the range. We have:
The range \(R\) of a function \(f\) is a subset of the codomain given by \(R=\{f(x) \,|\, x\text{ in the domain of }f\}\). That is, the range is the set of all outputs.
Some authors use a slightly different convention by calling the range what we called the codomain above.
Since we will be dealing with many functions it is convenient to name various functions (usually with letters \(f, g, h\), etc). Often we will implicitly assume that a domain and codomain are given without specifying these explicitly. If the range can be determined and the codomain is not given explicitly, then we take the codomain to be the range. If the range can not easily be determined and the codomain is not explicitly given, then the codomain should be taken to be a ‘simple’ set which clearly contains the range.
There are several ways to represent a particular function (all of which may not apply to a specific function): via a table of values (listing the input-output pairs), via a formula (with the domain and range explicitly or implicitly given), via a graph (representing input-output pairs on a coordinate plane), or in words, just to name a few. We have seen examples of the first three of these in previous sections. Our discussion in this section goes into greater detail.
Define the assignment \(f\) by the following table:
\[\begin{array}{|c||c|c|c|c|c|c|}
\hline x & 2 & 5 & -3 & 0 & 7 & 4 \\
\hline \hline y & 6 & 8 & 6 & 4 & -1 & 8 \\
\hline
\end{array} \nonumber \]
Solution
The assignment \(f\) assigns to the input \(2\) the output \(6\), which is also written as
\[f(2)=6 \nonumber \]
Similarly, \(f\) assigns to \(5\) the number \(8\), in short \(f(5)=8\), etc:
\[f(5)=8,\quad f(-3)=6,\quad f(0)=4,\quad f(7)=-1,\quad f(4)=8 \nonumber \]
The domain \(D\) is the set of all inputs. The domain is therefore
\[D=\{-3,0,2,4,5,7\}\nonumber \]
The range \(R\) is the set of all outputs. The range is therefore
\[R=\{-1,4,6,8\}\nonumber \]
The assignment \(f\) is indeed a function since each element of the domain gets assigned exactly one element in the range. Note that for an input number that is not in the domain, \(f\) does not assign an output to it. For example,
\[f(1)=\text{undefined}\nonumber \]
Note also that \(f(5)=8\) and \(f(4)=8\), so that \(f\) assigns to the inputs \(5\) and \(4\) the same output \(8\). Similarly, \(f\) also assigns the same output to the inputs \(2\) and \(-3\). Therefore we see that:
- A function may assign the same output to two different inputs!
Consider the assignment \(f\) that is given by the following table.
\[\begin{array}{|c||c|c|c|c|c|c|}
\hline x & 2 & 5 & -3 & 0 & 5 & 4 \\
\hline \hline y & 6 & 8 & 6 & 4 & -1 & 8 \\
\hline
\end{array} \nonumber \]
This assignment does not define a function! What went wrong?
Solution
Consider the input value \(5\). What does \(f\) assign to the input \(5\)? The third column states that \(f\) assigns to \(5\) the output \(8\), whereas the sixth column states that \(f\) assigns to \(5\) the output \(-1\),
\[f(5)=8, \quad\quad f(5)=-1 \nonumber \]
However, by the definition of a function, to each input we have to assign exactly one output. So, here, to the input \(5\) we have assigned two outputs \(8\) and \(-1\). Therefore, \(f\) is not a function.
- A function cannot assign two outputs to one input!
We repeat the two bullet points from the last two examples, which are crucial for the understanding of a function.
- \(f\left(x_{1}\right)=y\) and \(f\left(x_{2}\right)=y\) with \(x_{1} \neq x_{2}\) is allowed!
- \(f(x)=y_1\) and \(f(x)=y_2\) with \(y_{1} \neq 2_{2}\) is not allowed!
A university creates a mentoring program, which matches each freshman student with a senior student as his or her mentor. Within this program it is guaranteed that each freshman gets precisely one mentor, however two freshmen may receive the same mentor. Does the assignment of freshmen to mentor, or mentor to freshmen describe a function? If so, what is its domain, what is its range?
Solution
Since a senior may mentor several freshman, we cannot take a mentor as an “input,” as he or she would be assigned to several “output” freshmen students. So freshman is not a function of mentor.
On the other hand, we can assign each freshmen to exactly one mentor, which therefore describes a function. The domain (the set of all inputs) is given by the set of all freshmen students. The range (the set of all outputs) is given by the set of all senior students that are mentors. The function assigns each “input” freshmen student to his or her unique “output” mentor.
The rainfall in a city for each of the 12 months is displayed in the following histogram.
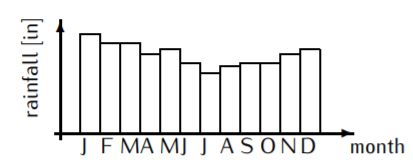
- Is the rainfall a function of the month?
- Is the month a function of the rainfall?
Solution
- Each month has exactly one amount of rainfall associated to it. Therefore, the assignment that associates to a month its rainfall (in inches) is a function.
- If we take a certain rainfall amount as our input data, can we associate a unique month to it? For example, February and March have the same amount of rainfall. Therefore, to one input amount of rainfall we cannot assign a unique month. The month is not a function of the rainfall.
Consider the function \(f\) described below.
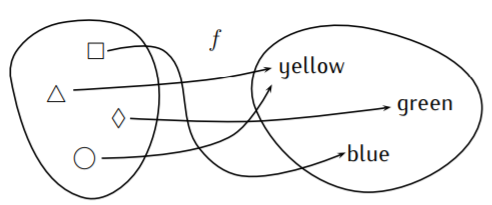
Here, the function \(f\) maps the input symbol \(\Box\) to the output color blue. Other assignments of \(f\) are as follows:
\[\begin{aligned} f(\Box)=\text{blue}, \quad\quad\,\,\, & f(\triangle)=\text{yellow} \\ f(\Diamond)=\text{green}, \quad\quad& f(\bigcirc)=\text{yellow}\end{aligned}\]
What is the Domain and Range of function f?
Solution
The domain is the set of symbols \(D=\{\Box,\triangle, \Diamond, \bigcirc\}\), and the range is the set of colors \(R=\{\)blue\(,\) green\(,\) yellow\(\}\). Notice, in particular, that the inputs \(\triangle\) and \(\bigcirc\) both have the same output yellow, which is certainly allowed for a function.
Consider the function \(y=5x+4\) with domain all real numbers and range all real numbers. Note that for each input \(x\), we obtain an exactly one induced output \(y\). For example, for the input \(x=3\) we get the output \(y=5\cdot 3+4=19\), etc.
Consider the function \(y=x^2\) with domain all real numbers and range non-negative numbers. The function takes a real number as an input and squares it. For example if \(x=-2\) is the input, then \(y=4\) is the output.
For each real number \(x\), denote by \(\lfloor x\rfloor\) the greatest integer that is less or equal to \(x\). We call \(\lfloor x\rfloor\) the floor of \(x\). For example, to calculate \(\lfloor4.37\rfloor\), note that all integers \(4, 3, 2, \dots\) are less or equal to \(4.37\):
\[\dots,-3,-2,-1,0,1,2,3,4\quad\quad \leq \quad 4.37 \nonumber \]
The greatest of these integers is \(4\), so that \(\lfloor 4.37\rfloor=4\). We define the floor function as \(f(x)=\lfloor x\rfloor\). Here are more examples of function values of the floor function.
\[\begin{aligned} && \lfloor 7.3\rfloor=7, \quad\quad\quad\,\, \lfloor \pi\rfloor=3, \quad\quad\quad\,\, \lfloor -4.65\rfloor=-5, \\ && \lfloor 12\rfloor=12, \quad\quad\quad \left\lfloor \frac{-26}{3}\right\rfloor= \lfloor -8.667\rfloor=-9 \end{aligned}\]
The domain of the floor function is the set of all real numbers, that is \(D=\mathbb{R}\). The range is the set of all integers, \(R=\mathbb{Z}\).
Let \(A\) be the area of an isosceles right triangle with base side length \(x\). Express \(A\) as a function of \(x\).
Solution
Being an isosceles right triangle means that two side lengths are \(x\), and the angles are \(45^\circ\), \(45^\circ\), and \(90^\circ\) (or in radian measure \(\dfrac\pi 4\), \(\dfrac\pi 4\), and \(\dfrac\pi 2\)):
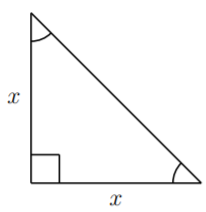
Recall that the area of a triangle is: area = \(\dfrac 1 2\) base \(\cdot\) height. In this case, we have base\(=x\), and height\(=x\), so that the area
\[A = \dfrac 1 2 x \cdot x = \dfrac 1 2 x^2 \nonumber \]
Therefore, the area \(A(x)=\dfrac 1 2 \cdot x^2\).
Consider the equation \(y=x^2+3\). Find the domain and range.
Solution
This equation associates to each input number \(a\) exactly one output number \(b=a^2+3\). Therefore, the equation defines a function. For example:
\[\text{To the input }5 \text{ we assign the output } 5^2+3=25+3=28 \nonumber \]
The domain \(D\) is all real numbers, \(D=\mathbb{R}\). Since \(x^2\) is always \(\geq 0\), we see that \(x^2+3\geq 3\), and vice versa every number \(y\geq 3\) can be written as \(y=x^2+3\). (To see this, note that the input \(x=\sqrt{y-3}\) for \(y\geq 3\) gives the output \(x^2-3=(\sqrt{y-3})^2+3=y-3+3=y\).) Therefore, the range is \(R=[3,\infty)\).
Consider the equation \(x^2+y^2=25\). Does this equation define \(y\) as a function of \(x\)? That is, does this equation assign to each input \(x\) exactly one output \(y\)?
Solution
An input number \(x\) gets assigned to \(y\) with \(x^2+y^2=25\). Solving this for \(y\), we obtain
\[y^2=25-x^2 \quad\implies\quad y=\pm\sqrt{25-x^2} \nonumber \]
Therefore, there are two possible outputs associated to the input \(x(\not=5)\):
\[\text{either }\quad y=+\sqrt{25-x^2} \quad \quad \text{ or } \quad y=-\sqrt{25-x^2} \nonumber \]
For example, the input \(x=0\) has two outputs \(y=5\) and \(y=-5\). However, a function cannot assign two outputs to one input \(x\)! The conclusion is that \(x^2+y^2=25\) does not determine \(y\) as a function!
Note that if \(y=f(x)\) then \(x\) is called the independent variable and \(y\) is called the dependent variable (since it depends on \(x\)). If \(x=g(y)\) then \(y\) is the independent variable and \(x\) is the dependent variable (since it depends on \(y\)).