8.6.1: Parametric Equations (Exercise)
- Page ID
- 22248
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)section 8.6 exercises
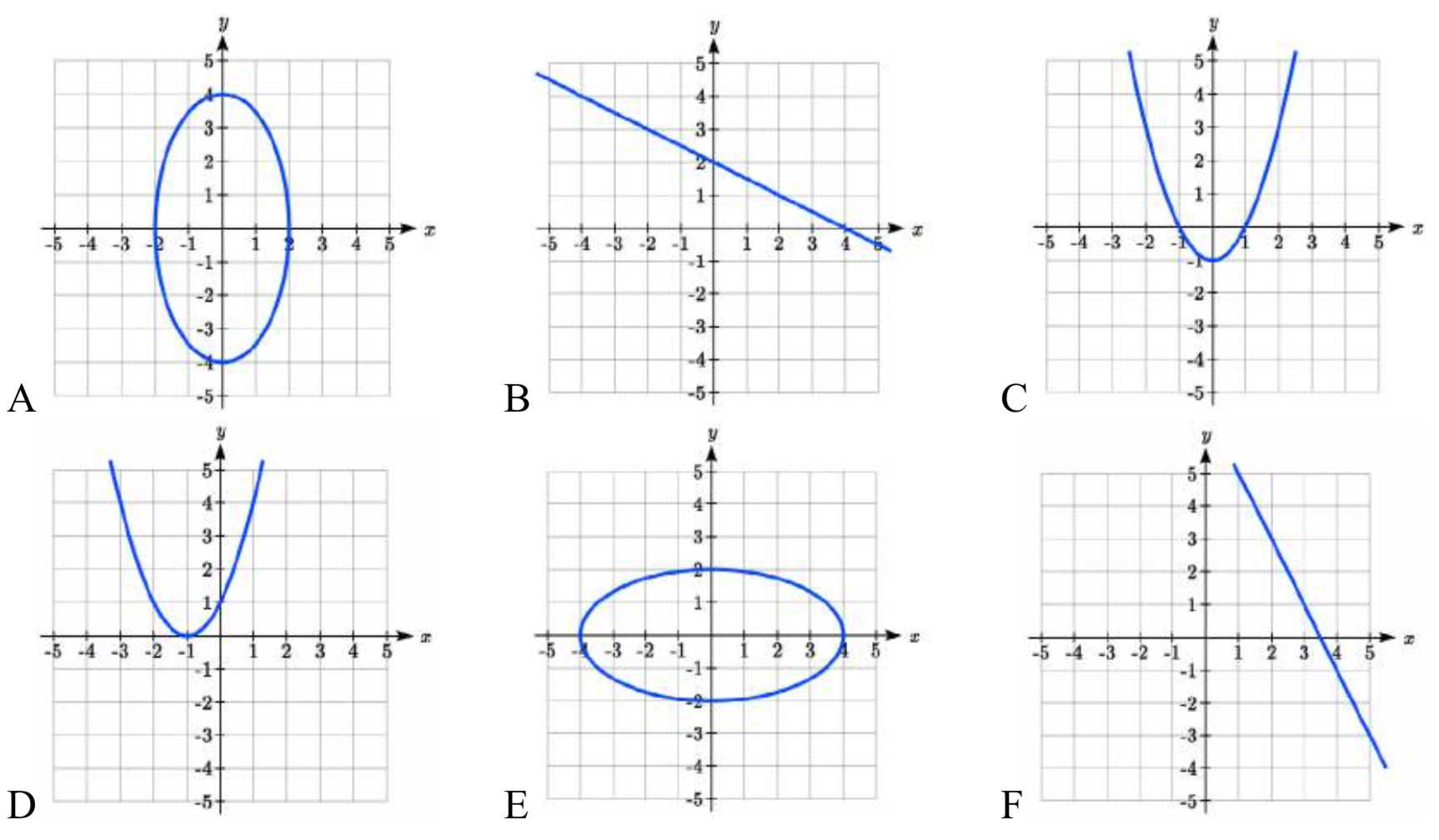
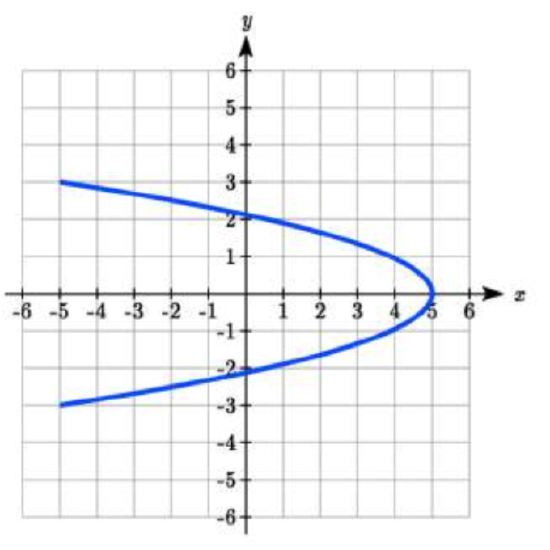
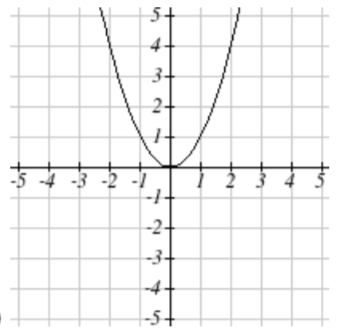
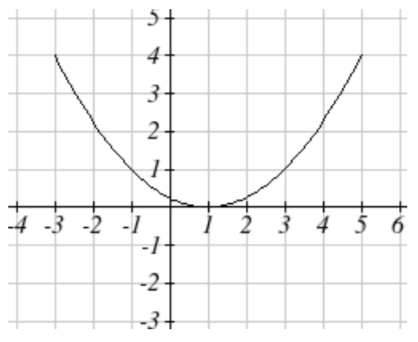
Match each set of equation with one of the graphs below.
1. \(\begin{cases} x(t) = t \\ y(t) = t^2 - 1 \end{cases}\)
2. \(\begin{cases} x(t) = t - 1 \\ y(t) = t^2 \end{cases}\)
3. \(\begin{cases} x(t) = 4\sin(t) \\ y(t) = 2\cos(t) \end{cases}\)
4. \(\begin{cases} x(t) = 2\sin(t) \\ y(t) = 4\cos(t) \end{cases}\)
5. \(\begin{cases} x(t) = 2 + t \\ y(t) = 3 - 2t \end{cases}\)
6. \(\begin{cases} x(t) = -2 - t \\ y(t) = 3 + t \end{cases}\)
From each pair of graphs in the \(t-x\) and \(t-y\) planes shown, sketch a graph in the \(x-y\) plane.
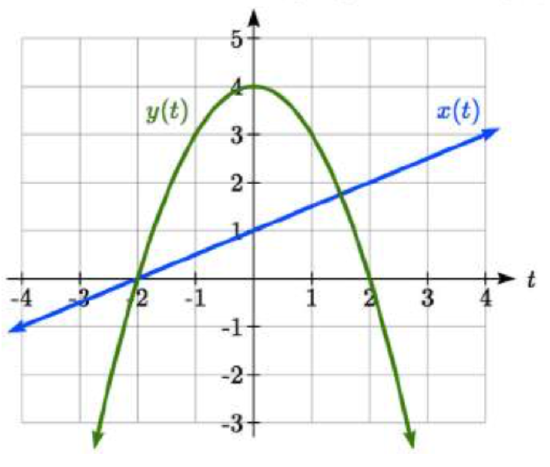
7. 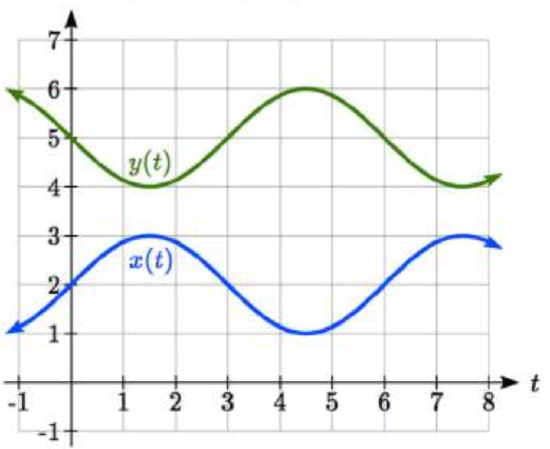 8.
8. 
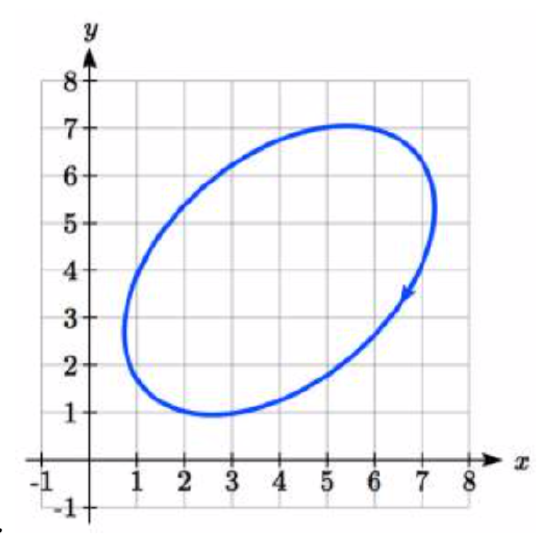
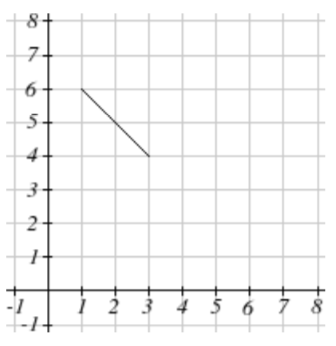
From each graph in the \(x-y\) plane shown, sketch a graph of the parameter functions in the \(t-x\) and \(t-y\) planes.
9. 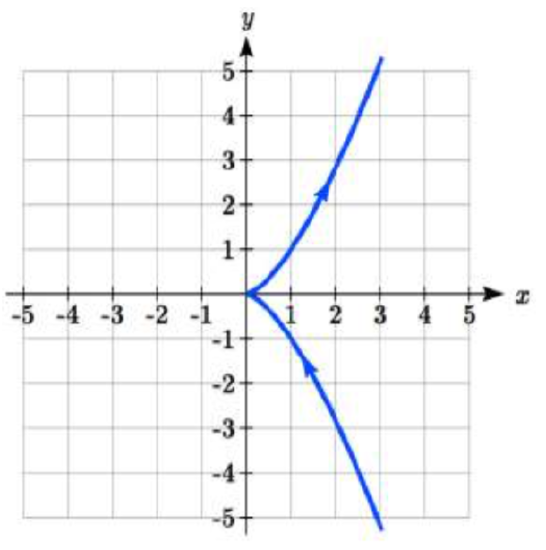 10.
10. 
Sketch the parametric equations for \(-2 \le t \le 2\).
11. \(\begin{cases} x(t) = 1 + 2t \\ y(t) = t^2 \end{cases}\)
12. \(\begin{cases} x(t) = 2t - 2 \\ y(t) = t^3 \end{cases}\)
Eliminate the parameter \(t\) to rewrite the parametric equation as a Cartesian equation
13. \(\begin{cases} x(t) = 5 - t \\ y(t) = 8 - 2t \end{cases}\)
14. \(\begin{cases} x(t) = 1 + 2t \\ y(t) = 10 - t \end{cases}\)
15. \(\begin{cases} x(t) = 2t + 1 \\ y(t) = 3\sqrt{t} \end{cases}\)
16. \(\begin{cases} x(t) = 3t - 1 \\ y(t) = 2t^2 \end{cases}\)
17. \(\begin{cases} x(t) = 2e^t \\ y(t) = 1 - 5t \end{cases}\)
18. \(\begin{cases} x(t) = 4\text{log} (t) \\ y(t) = 3 + 2t \end{cases}\)
19. \(\begin{cases} x(t) = t^3 - t \\ y(t) = 2t \end{cases}\)
20. \(\begin{cases} x(t) = t - t^4 \\ y(t) = t + 2 \end{cases}\)
21. \(\begin{cases} x(t) = e^{2t} \\ y(t) = e^{6t} \end{cases}\)
22. \(\begin{cases} x(t) = t^5 \\ y(t) = t^{10} \end{cases}\)
23. \(\begin{cases} x(t) = 4\cos(t) \\ y(t) = 5\sin(t) \end{cases}\)
24. \(\begin{cases} x(t) = 3\sin(t) \\ y(t) = 6\cos(t) \end{cases}\)
Parameterize (write a parametric equation for) each Cartesian equation
25. \(y(x) = 3x^2 + 3\)
26. \(y(x) = 2\sin(x) + 1\)
27. \(x(y) = 3 \text{log} (y) + y\)
28. \(x(y) = \sqrt{y} + 2y\)
29. \(\dfrac{x^2}{4} + \dfrac{y^2}{9} = 1\)
30. \(\dfrac{x^2}{16} + \dfrac{y^2}{36} = 1\)
Parameterize the graphs shown.
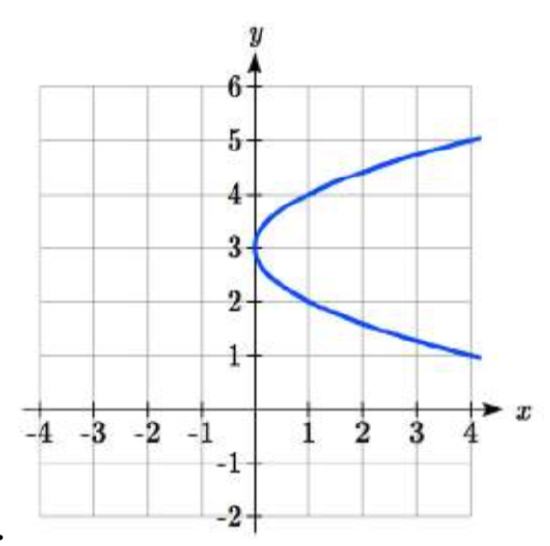
31. 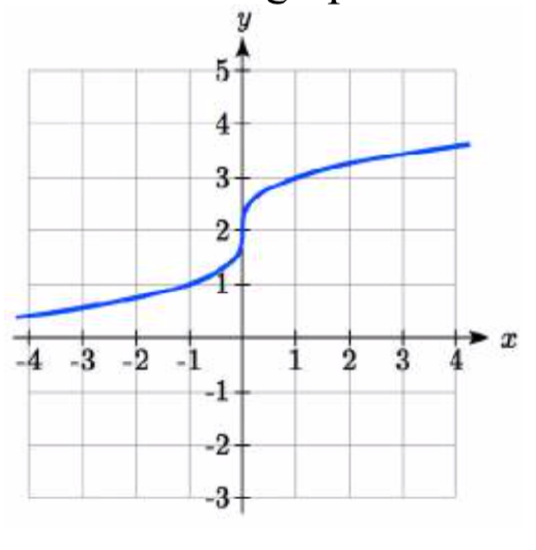 32.
32. 
33. 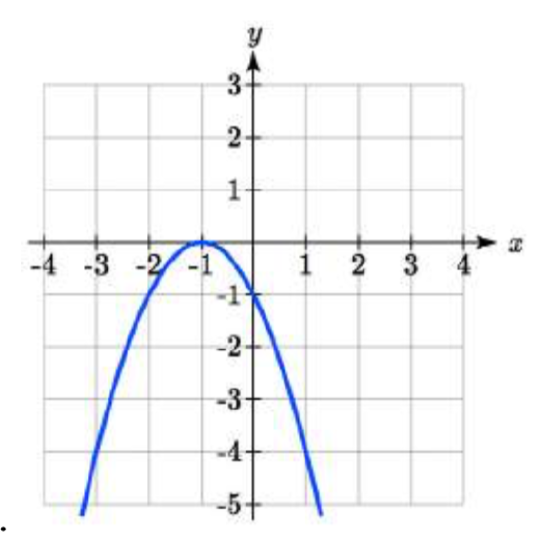 34.
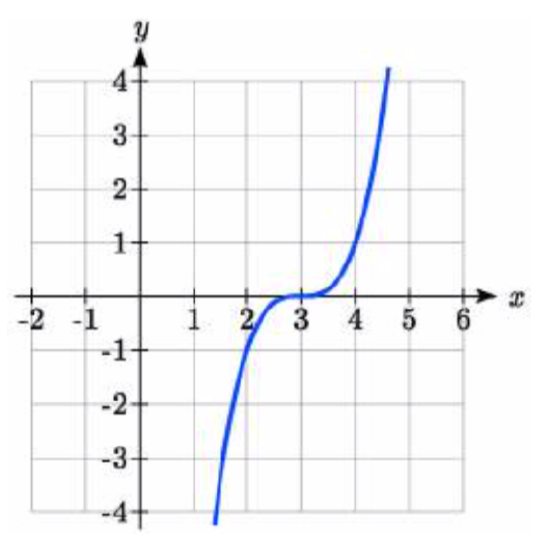
34. 
35. Parameterize the line from (−1,5) to (2,3) so that the line is at (−1,5) at \(t = 0\), and at (2,3) at \(t = 1\).
36. Parameterize the line from (4,1) to (6,−2) so that the line is at (4,1) at \(t = 0\), and at(6,−2) at \(t = 1\).
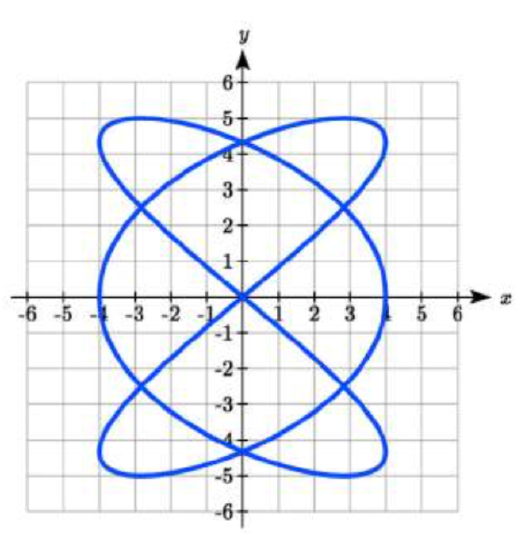
The graphs below are created by parameteric equations of the form \(\left\{\begin{array}{c}{x(t)=a\cos (bt)}\\{y(t)=c\sin (dt)}\end{array}\right.\). Find the values of \(a\), \(b\), \(c\), and \(d\) to achieve each graph.
37. 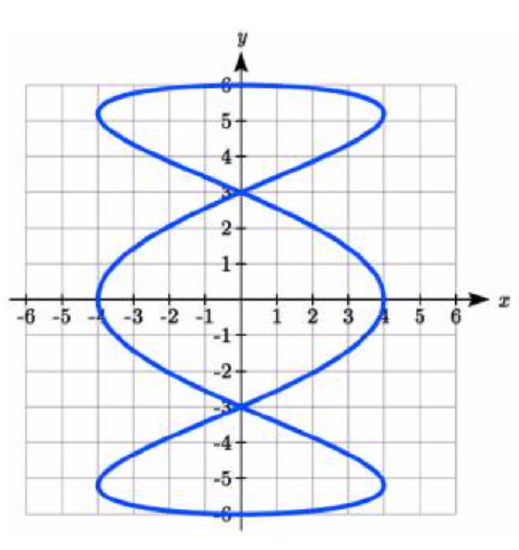 38.
38. 
39. 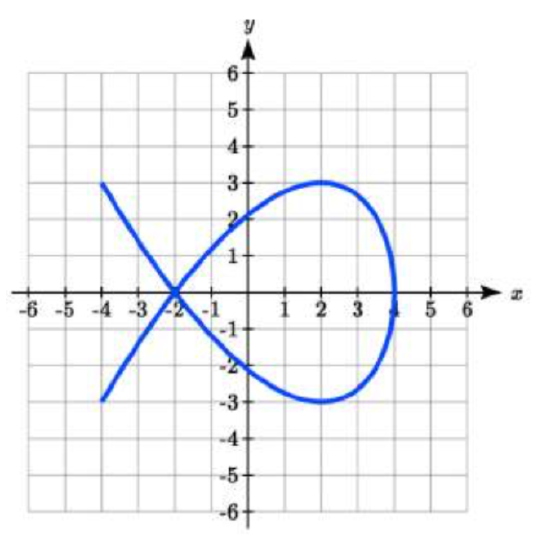 40.
40. 
41. An object is thrown in the air with vertical velocity 20 ft/s and horizontal velocity 15 ft/s. The object’s height can be described by the equation \(y (t) = -16t^2 + 20t\), while the object moves horizontally with constant velocity 15 ft/s. Write parametric equations for the object’s position, then eliminate time to write height as a function of horizontal position.
42. A skateboarder riding on a level surface at a constant speed of 9 ft/s throws a ball in the air, the height of which can be described by the equation \(y (t) = -16t^2 + 10t + 5\). Write parametric equations for the ball’s position, then eliminate time to write height as a function of horizontal position.
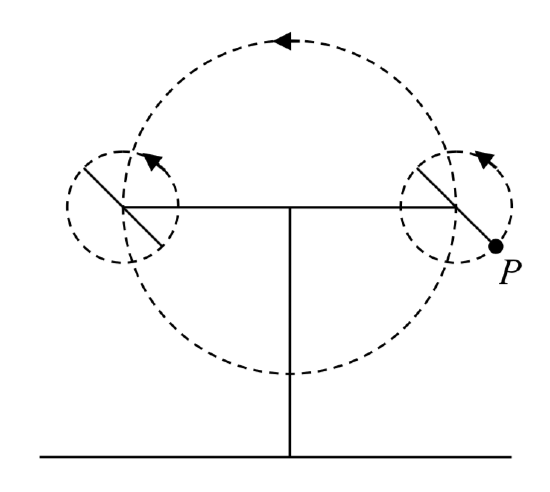
43. A carnival ride has a large rotating arm with diameter 40 feet centered 35 feet off the ground. At each end of the large arm are two smaller rotating arms with diameter 16 feet each. The larger arm rotates once every 5 seconds, while the smaller arms rotate once every 2 seconds. If you board the ride when the point \(P\) is closest to the ground, find parametric equations for your position over time.
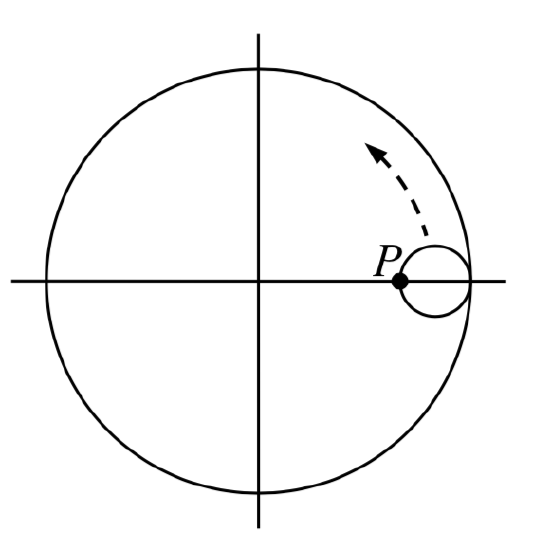
44. A hypocycloid is a shape generated by tracking a fixed point on a small circle as it rolls around the inside of a larger circle. If the smaller circle has radius 1 and the large circle has radius 6, find parametric equations for the position of the point \(P\) as the smaller wheel rolls in the direction indicated.
- Answer
-
1. C
3. E
5. F
7.
9. x(t)
 y(t)
y(t) 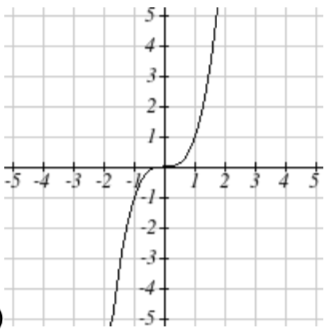
11.
13. \(y = -2 + 2x\)
15. \(y = 3\sqrt{\dfrac{x - 1}{2}}\)
17. \(y = x^3\)
19. \(x = (\dfrac{y}{2})^3 - \dfrac{y}{2}\)
21. \(y = x^3\)
23. \(\dfrac{x}{4})^2 + (\dfrac{y}{5})^2 = 1\)
25. \(\begin{cases} x(t) = t \\ y(t) = 3t^2 + 3 \end{cases}\)
27. \(\begin{cases} x(t) = 3\log(t) + t \\ y(t) = t \end{cases}\)
29. \(\begin{cases} x(t) = 2\cos(t) \\ y(t) = 3\sin(t) \end{cases}\)
31. \(\begin{cases} x(t) = t^3 \\ y(t) = 3t^2 + 3 \end{cases}\)
33. \(\begin{cases} x(t) = t - 1\\ y(t) = -t^2 \end{cases}\)
35. \(\begin{cases} x(t) = -1 + 3t \\ y(t) = 5 - 2t \end{cases}\)
37. \(\begin{cases} x(t) = 4\cos(3t) \\ y(t) = 6\sin(t) \end{cases}\)
39. \(\begin{cases} x(t) = 4\cos(2t) \\ y(t) = 3\sin(3t) \end{cases}\)
41. \(y(x) = -16 (\dfrac{x}{15})^2 + 20(\dfrac{x}{15})\)
43. \(\begin{cases} x(t) = 20\sin(\dfrac{2\pi}{5} t) + 8\sin(\pi t) \\ y(t) = 35 - 20 \cos(\dfrac{2\pi}{5}t) - 8\cos(\pi t) \end{cases}\)


