8.6: Parametric Equations
- Page ID
- 13880
Many shapes, even ones as simple as circles, cannot be represented as an equation where \(y\) is a function of \(x\). Consider, for example, the path a moon follows as it orbits around a planet, which simultaneously rotates around a sun. In some cases, polar equations provide a way to represent such a path. In others, we need a more versatile approach that allows us to represent both the \(x\) and \(y\) coordinates in terms of a third variable, or parameter.
Definition: Parametric Equations
A system of parametric equations is a pair of functions \(x(t)\) and \(y(t)\) in which the \(x\) and \(y\) coordinates are the output, represented in terms of a third input parameter, \(t\).
Example \(\PageIndex{1}\)
Moving at a constant speed, an object moves at a steady rate along a straight path from coordinates (-5, 3) to the coordinates (3, -1) in 4 seconds, where the coordinates are measured in meters. Find parametric equations for the position of the object.
Solution
The \(x\) coordinate of the object starts at -5 meters, and goes to +3 meters, this means the \(x\) direction has changed by 8 meters in 4 seconds, giving us a rate of 2 meters per second. We can now write the \(x\) coordinate as a linear function with respect to time, \(t\), \(x(t) = −5 + 2t\). Similarly, the \(y\) value starts at 3 and goes to -1, giving a change in \(y\) value of 4 meters, meaning the \(y\) values have decreased by 4 meters in 4 seconds, for a rate of -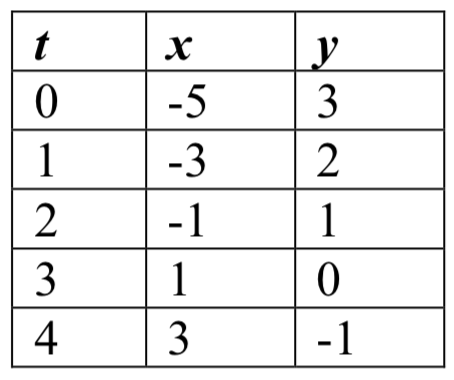 1 meter per nd, giving equation \(y(t)=3−t\). Together, these are the parametric equations for the position of the object:
1 meter per nd, giving equation \(y(t)=3−t\). Together, these are the parametric equations for the position of the object:
\[x(t) = -5 + 2t\nonumber\]
\[y(t) = 3 - t\nonumber\]
Using these equations, we can build a table of \(t\), \(x\), and \(y\) values. Because of the context, we limited ourselves to non-negative \(t\) values for this example, but in general you can use any values.
From this table, we could create three possible graphs: a graph of \(x\) vs. \(t\), which would show the horizontal position over time, a graph of \(y\) vs. \(t\), which would show the vertical position over time, or a graph of \(y\) vs. \(x\), showing the position of the object in the plane.
Position of \(x\) as a function of time Position of \(y\) as a function of time Position of \(y\) relative to \(x\)
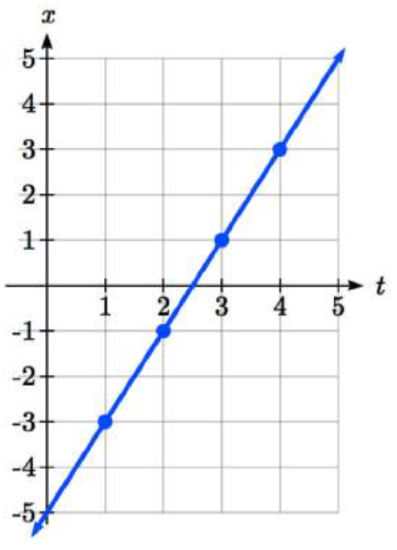
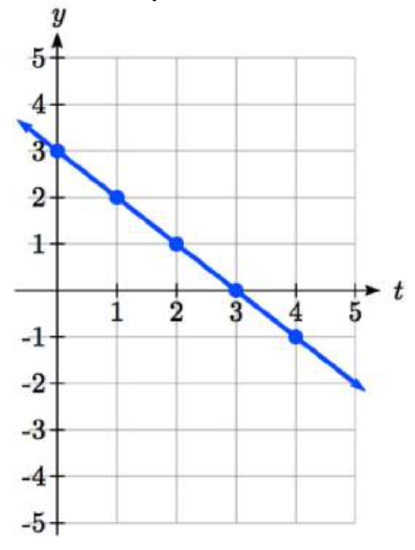
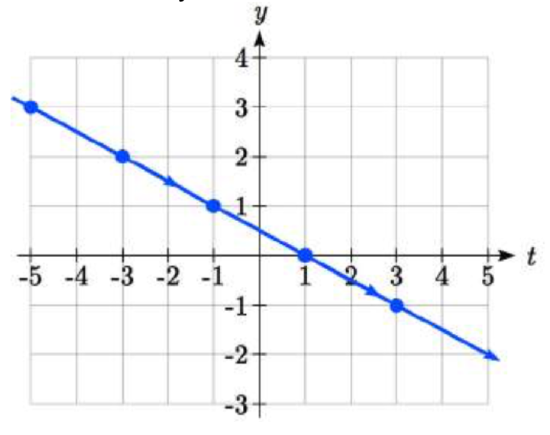
Notice that the parameter \(t\) does not explicitly show up in this third graph. Sometimes, when the parameter \(t\) does represent a quantity like time, we might indicate the direction of movement on the graph using an arrow, as shown above.
There is often no single parametric representation for a curve. In Example 1 we assumed the object was moving at a 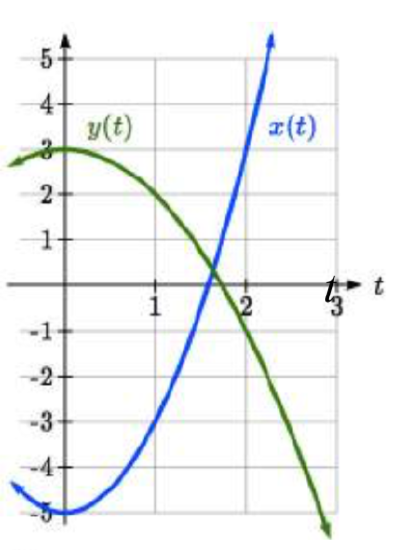 steady rate along a straight line. If we kept the assumption about the path (straight line) but did not assume the speed was constant, we might get a system like:
steady rate along a straight line. If we kept the assumption about the path (straight line) but did not assume the speed was constant, we might get a system like:
\[x(t) = -5 + 2t^2\nonumber\]
\[y(t) = 3 - t^2\nonumber\]
This starts at (-5, 3) when \(t = 0\) and ends up at (3, -1) when \(t = 2\). If we graph the \(x(t)\) and \(y(t)\) function separately, we can see that those are no longer linear, but if we graph \(x\) vs. \(y\) we will see that we still get a straight-line path.
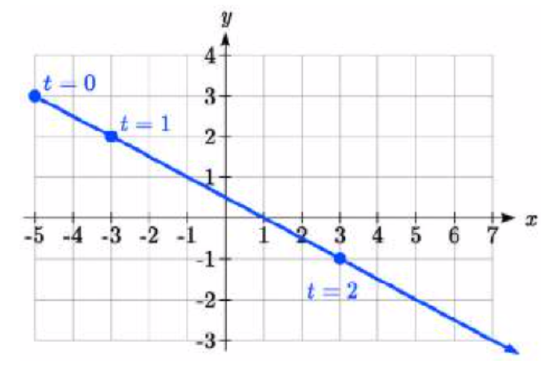
Example \(\PageIndex{2}\)
Sketch a graph of
\[x(t) = t^2 + 1\nonumber\]
\[y(t) = 2 + t\nonumber\]
Solution
We can begin by creating a table of values. From this table, we can plot the (\(x\), \(y\)) points in the plane, sketch in a rough gr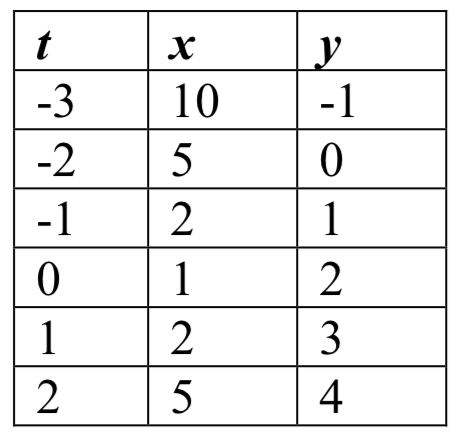 aph of the curve, and indicate the direction of motion with respect to time by using arrows.
aph of the curve, and indicate the direction of motion with respect to time by using arrows.
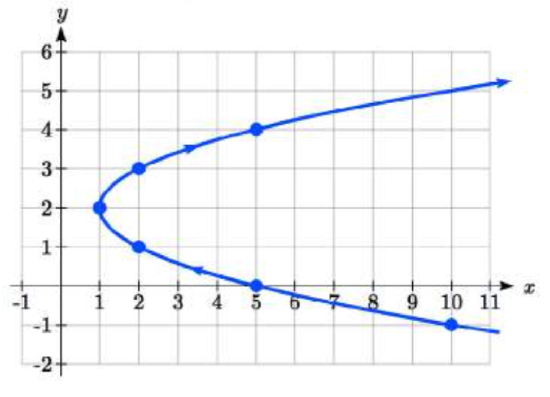
Notice that here the parametric equations describe a shape for which \(y\) is not a function of \(x\). This is an example of why using parametric equations can be useful – since they can represent such a graph as a set of functions. This particular graph also appears to be a parabola where \(x\) is a function of \(y\), which we will soon verify.
Example \(\PageIndex{3}\)
Sketch a graph of
\[x(t) = 3\cos(t)\nonumber\]
\[y(t) = 3\sin(t)\nonumber\]
Solution
These equations should look familiar. Back when we first learned about sine and cosine we found that the coordinates o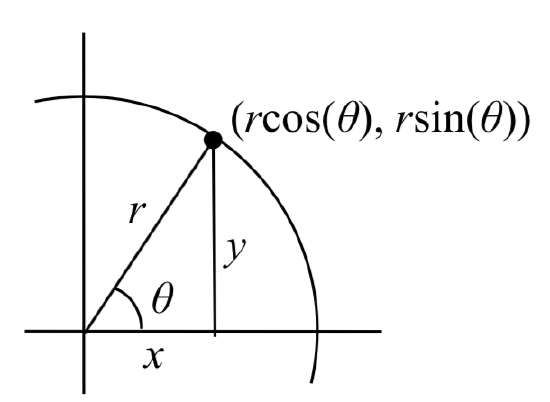 f a point on a circle of radius \(r\) at an angle of \(\theta\) will be \(x = r \cos(\theta), y r \sin(\theta)\). The equations above are in the same form, with \(r =3\), and \(t\) used in place of \(\theta\).
f a point on a circle of radius \(r\) at an angle of \(\theta\) will be \(x = r \cos(\theta), y r \sin(\theta)\). The equations above are in the same form, with \(r =3\), and \(t\) used in place of \(\theta\).
This suggests that for each value of \(t\), these parametric equations give a point on a circle of ra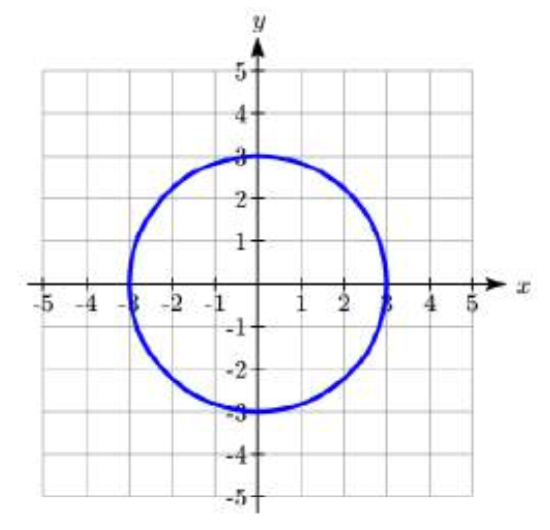 dius 3 at the angle corresponding to \(t\). At \(t = 0\), the graph would be at \(x = 3\cos(0), y = 3\sin(0)\), the point (3,0). Indeed, these equations describe the equation of a circle, drawn counterclockwise.
dius 3 at the angle corresponding to \(t\). At \(t = 0\), the graph would be at \(x = 3\cos(0), y = 3\sin(0)\), the point (3,0). Indeed, these equations describe the equation of a circle, drawn counterclockwise.
Interestingly, these similar parametric equations also describe the circle of radius 3:
\[x(t) = 3\sin(t)\nonumber\]
\[y(t) = 3\cos(t)\nonumber\]
The difference with these equations it the graph would start at \(x = 3\sin(0)\), \(y = 3\cos(0)\), the point (0, 3). As \(t\) increases from 0, the \(x\) value will increase, indicating these equation would draw the graph in a clockwise direction.
While creating a \(t-x-y\) table, plotting points and connecting the dots with a smooth curve usually works to give us a rough idea of what the graph of a system of parametric equations looks like, it's generally easier to use technology to create these tables and (simultaneously) much nicer-looking graphs.
Example \(\PageIndex{4}\)
Sketch a graph of \(\begin{array} {rcl} {x(t)} &= & {2\cos(t)} \\ {y(t)} &= & {3\sin(t)} \end{array}\)
Solution
Notice first that this equation looks very similar to the ones from the previous example, except the coefficients are not equ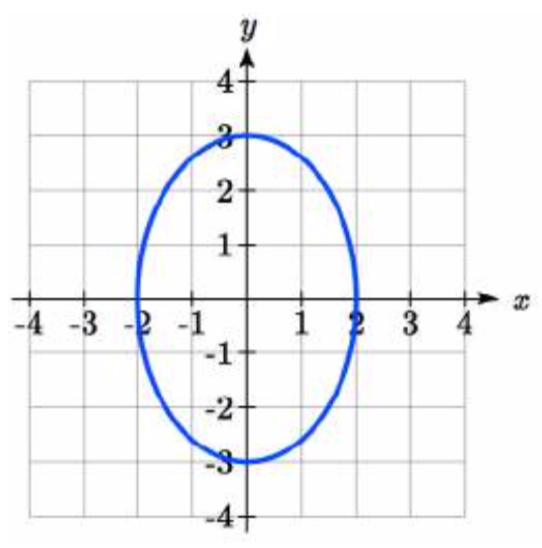 al. You might guess that the pairing of cos and sin will still produce rotation, but now \(x\) will vary from -2 to 2 while \(y\) will vary from -3 to 3, creating an ellipse.
al. You might guess that the pairing of cos and sin will still produce rotation, but now \(x\) will vary from -2 to 2 while \(y\) will vary from -3 to 3, creating an ellipse.
Using technology we can generate a graph of this equation, verifying it is indeed an ellipse.
Similar to graphing polar equations, you must change the MODE on your calculator (or select parametric equations on your graphing technology) before graphing a system of parametric equations. You will know you have successfully entered parametric mode when the equation input has changed to ask for a \(x(t)=\) and \(y(t)=\) pair of equations.
Exercise \(\PageIndex{1}\)
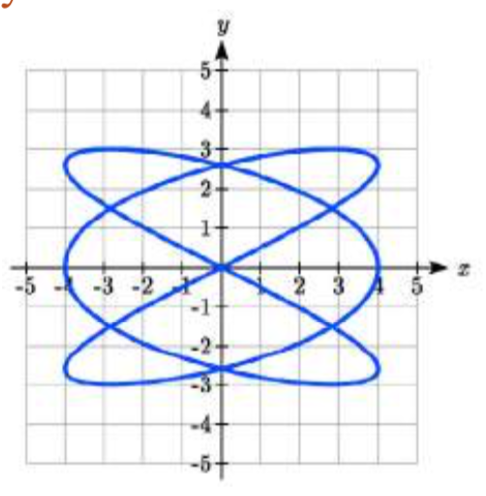
Sketch a graph of \(\begin{array} {rcl} {x(t)} &= & {4\cos(3t)} \\ {y(t)} &= & {3\sin(2t)} \end{array}\). This is an example of a Lissajous figure.
- Answer
-
Example \(\PageIndex{5}\)
The populations of rabbits and wolves on an island over time are given by the graphs below. Use these graphs to sketch a graph in the r-w plane showing the relationship between the number of rabbits and number of wolves.
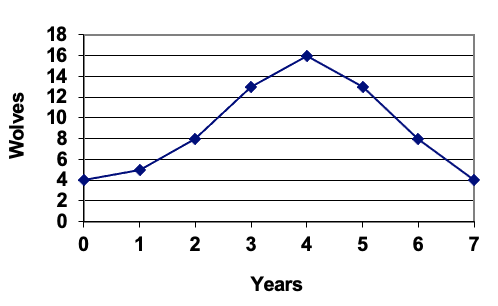
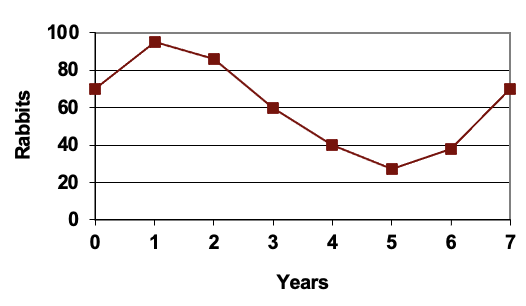
Solution
For each input \(t\), we can determine the number of rabbits, \(r\), and the number of wolves, \(w\), from the respective graphs, and then plot the corresponding point in the \(r-w\) plane.
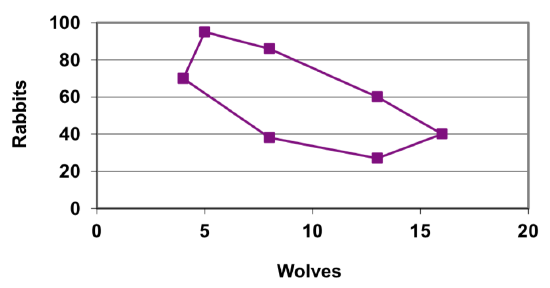
This graph helps reveal the cyclical interaction between the two populations.
Converting from Parametric to Cartesian
In some cases, it is possible to eliminate the parameter \(t\), allowing you to write a pair of parametric equations as a Cartesian equation.
It is easiest to do this if one of the \(x(t)\) or \(y(t)\) functions can easily be solved for \(t\), allowing you to then substitute the remaining expression into the second part.
Example \(\PageIndex{6}\)
Write \(\begin{array} {rcl} {x(t)} &= & {t^2 + 1} \\ {y(t)} &= & {2 + t} \end{array}\) as a Cartesian equation, if possible.
Solution
Here, the equation for \(y\) is linear, so is relatively easy to solve for \(t\). Since the resulting Cartesian equation will likely not be a function, and for convenience, we drop the function notation.
\[y = 2 + t\nonumber\]Solve for \(t\)
\[y - 2 = t\nonumber\]Substitute this for \(t\) in the \(x\) equation
\[x = (y - 2)^2 + 1\nonumber\]
Notice that this is the equation of a parabola with \(x\) as a function of \(y\), with vertex at (1,2), opening to the right. Comparing this with the graph from Example 2, we see (unsurprisingly) that it yields the same graph in the \(x-y\) plane as did the original parametric equations.
Exercise \(\PageIndex{2}\)
Write \(\begin{array} {rcl} {x(t)} &= & {t^3} \\ {y(t)} &= & {t^6} \end{array}\) as a Cartesian equation, if possible.
- Answer
-
\[y = (t^3)^2\text{, so }y = x^2\nonumber\]
Example \(\PageIndex{7}\)
Write \(\begin{array} {x(t)} &= & {\sqrt{t} + 2} \\ {y(t)} &= & {\text{log}(t)} \end{array}\) as a Cartesian equation, if possible.
Solution
We could solve either the first or second equation for \(t\). Solving the first,
\[x = \sqrt{t} + 2\nonumber\]
\[x - 2 = \sqrt{t}\nonumber\]Square both sides
\[(x - 2)^2 = t\nonumber\]Substitute into the \(y\) equation
\[y = \text{log} ((x - 2)^2)\nonumber\]
Since the parametric equation is only defined for \(t > 0\), this Cartesian equation is equivalent to the parametric equation on the corresponding domain. The parametric equations show that when \(t > 0\), \(x > 2\) and \(y > 0\), so the domain of the Cartesian equation should be limited to \(x > 2\).
To ensure that the Cartesian equation is as equivalent as possible to the original parametric equation, we try to avoid using domain-restricted inverse functions, such as the inverse trig functions, when possible. For equations involving trig functions, we often try to find an identity to utilize to avoid the inverse functions.
Example \(\PageIndex{8}\)
Write \(\begin{array} {rcl} {x(t)} &= & {2\cos(t)} \\ {y(t)} &= & {3\sin(t)} \end{array}\) as a Cartesian equation, if possible.
Solution
To rewrite this, we can utilize the Pythagorean identity \(\cos^2(t) + \sin^2(t) = 1\).
\[x = 2\cos(t)\text{ so }\dfrac{x}{2} = \cos(t)\nonumber\]
\[y = 3\sin(t)\text{ so }\dfrac{y}{3} = \sin(t)\nonumber\]
Starting with the Pythagorean identity,
\[\cos^2(t) + \sin^2(t) = 1\nonumber\]Substitute in the expressions from the parametric form
\[(\dfrac{x}{2})^2 + (\dfrac{y}{3})^2 = 1\nonumber\]Simplify
\[\dfrac{x^2}{4} + \dfrac{y^2}{9} = 1\nonumber\]
This is a Cartesian equation for the ellipse we graphed earlier.
Parameterizing Curves
While converting from parametric form to Cartesian can be useful, it is often more useful to parameterize a Cartesian equation – converting it into parametric form.
If the Cartesian equation gives one variable as a function of the other, then parameterization is trivial – the independent variable in the function can simply be defined as \(t\).
Example \(\PageIndex{9}\)
Parameterize the equation \(x = y^3 - 2y\).
Solution
In the equation, \(x\) is expressed as a function of \(y\). By defining \(y = t\) we can then substitute that into the Cartesian equation, yielding \(x = t^3 - 2t\). Together, this produces the parametric form:
\[x(t) = t^3 - 2t\nonumber\]
\[y(t) = t\nonumber\]
Exercise \(\PageIndex{3}\)
Write \(x^2 + y^2 = 3\) in parametric form, if possible.
- Answer
-
\[\begin{array} {rcl} {x(t)} &= & {3\cos(t)} \\ {y(t)} &= & 3\sin(t) \end{array}\nonumber\]
In addition to parameterizing Cartesian equations, we also can parameterize behaviors and movements.
Example \(\PageIndex{10}\)
A robot follows the path shown. Create a table of values for the \(x(t)\) and \(y(t)\) functions, assuming the robot takes one second to make each movement.
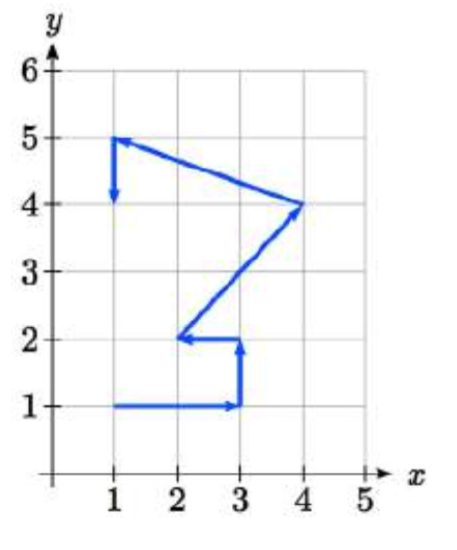
Solution
Since we know the direction of motion, we can introduce consecutive values for \(t\) along the path of the robot. Using these values with the \(x\) and \(y\) coordinates of the robot, we can create the tables. For example, we designate the starting point, at (1, 1), as the position at \(t = 0\), the next point at (3, 1) as the position at \(t = 1\), and so on.

Notice how this also ties back to vectors. The journey of the robot as it moves through the Cartesian plane could also be displayed as vectors and total distance traveled and displacement could be calculated.
Example \(\PageIndex{11}\)
A light is placed on the edge of a bicycle tire as shown and the bicycle starts rolling down the street. Find a parametric equation for the position of the light after the wheel has rotated through an angle of \(\theta\).
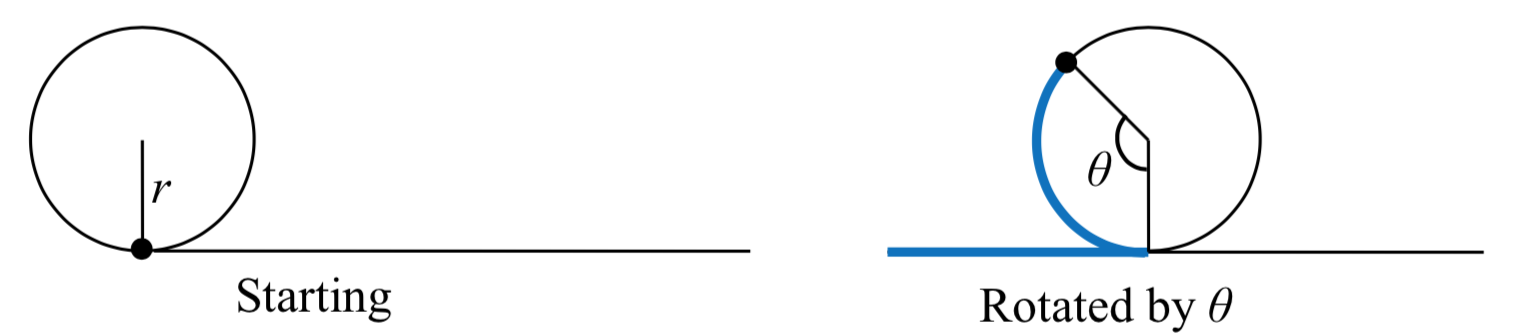
Solution
Relative to the center of the wheel, the position of the light can be found as the coordinates of a point on a circle, but since the \(x\) coordinate begins at 0 and moves in the negative direction, while the \(y\) coordinate starts at the lowest value, the coordinates of the point will be given by:
\[x = -r\sin(\theta)\nonumber\]
\[y = -r\cos(\theta)\nonumber\]
The center of the wheel, meanwhile, is moving horizontally. It remains at a constant height of \(r\), but the horizontal position will move a distance equivalent to the arclength of the circle drawn out by the angle, \(s = r\theta\). The position of the center of the circle is then
\[x = r\theta\nonumber\]
\[y = r\nonumber\]
Combining the position of the center of the wheel with the position of the light on the wheel relative to the center, we get the following parametric equationw, with \(\theta\) as the parameter:
\[x = r\theta - r\sin(\theta) = r(\theta - \sin(\theta))\nonumber\]
\[y = r - r\cos(\theta) = r(1 - \cos(\theta))\nonumber\]
The result graph is called a cycloid.
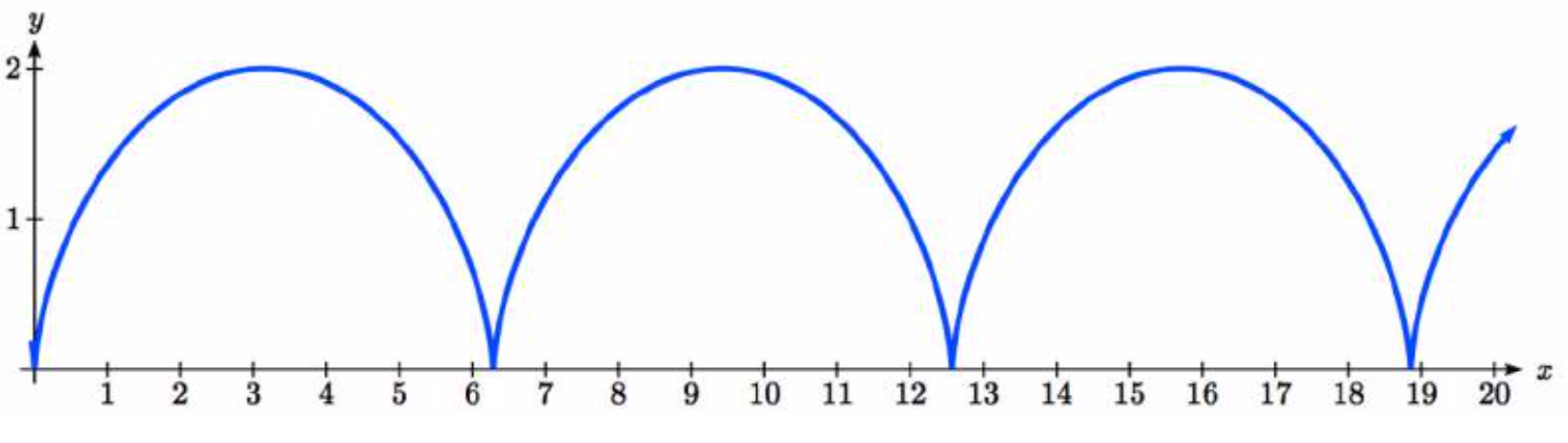
Example \(\PageIndex{12}\)
A moon travels around a planet as shown, orbiting once every 10 days. The planet travels around a sun as shown, orbiting once every 100 days. Find a parametric equation for the position of the moon, relative to the center of the sun, after \(t\) days.
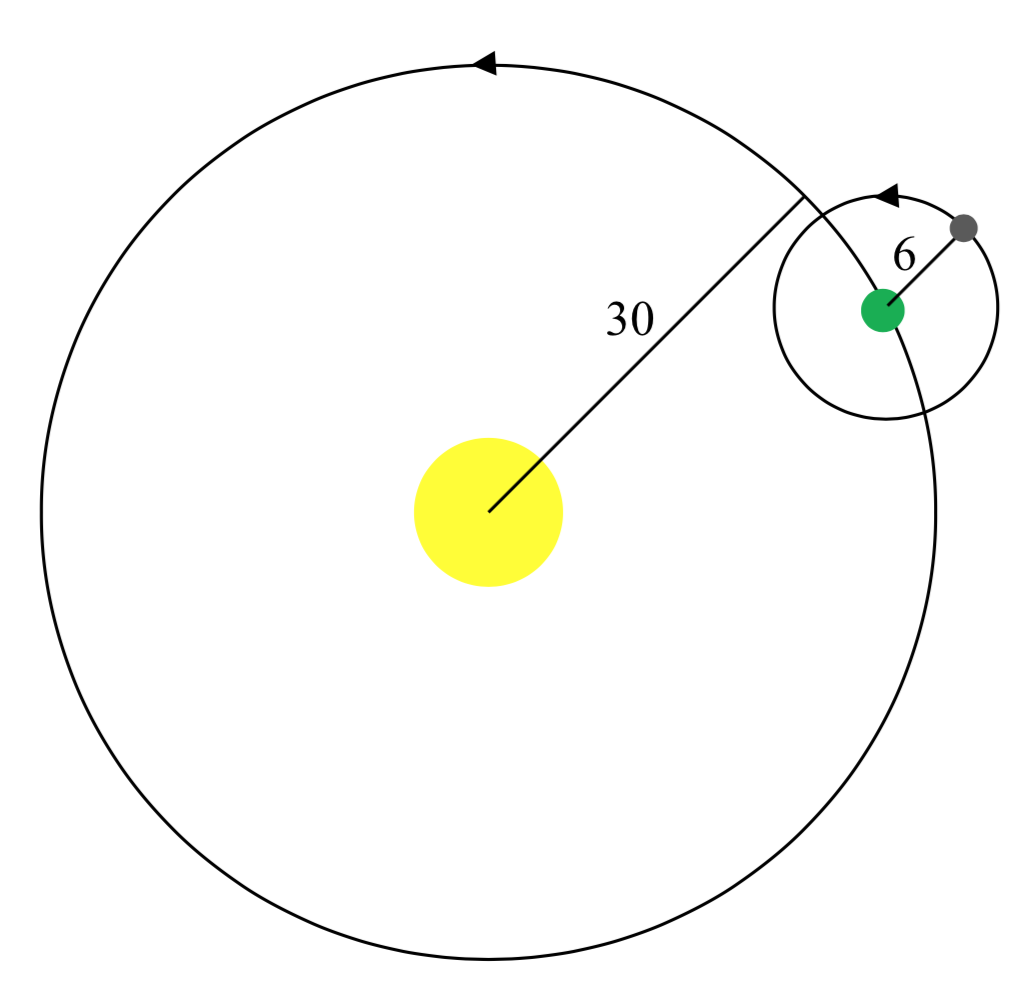
Solution
For this example, we’ll assume the orbits are circular, though in real life they’re actually elliptical.
The coordinates of a point on a circle can always be written in the form
\[x = r\cos(\theta)\nonumber\]
\[y = r\sin(\theta)\nonumber\]
Since the orbit of the moon around the planet has a period of 10 days, the equation for the position of the \(moon\) \(relative\) \(to\) \(the\) \(planet\)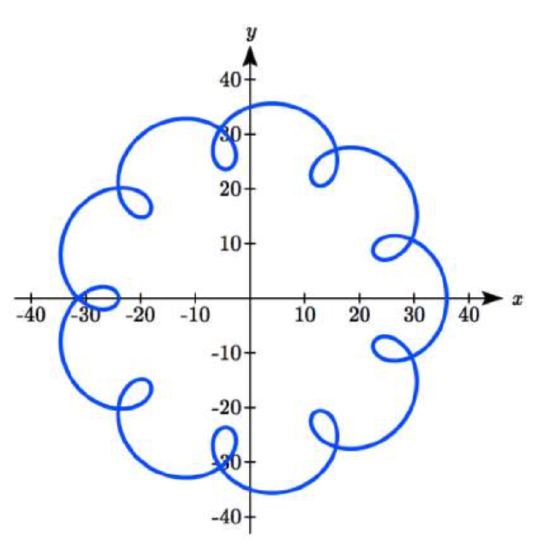 will be
will be
\[x(t) = 6\cos(\dfrac{2\pi}{10}t) = 6\cos(\dfrac{\pi}{5}t)\nonumber\]
\[y(t) = 6\sin(\dfrac{2\pi}{10}t) = 6\sin(\dfrac{\pi}{5}t)\nonumber\]
With a period of 100 days, the equation for the position of the \(planet\) \(relative\) \(to\) \(the\) \(sun\) will be
\[x(t) = 30\cos(\dfrac{2\pi}{100} t) = 30 \cos (\dfrac{\pi}{50} t)\nonumber\]
\[y(t) = 30\sin(\dfrac{2\pi}{100} t) = 30 \sin (\dfrac{\pi}{50} t)\nonumber\]
Combining these together, we can find the position of the \(moon\) \(relative\) \(to\) \(the\) \(sun\) as the sum of the components.
\[x(t) = 6\cos(\dfrac{2\pi}{5} t) = 30 \cos (\dfrac{\pi}{50} t)\nonumber\]
\[y(t) = 6\cos(\dfrac{2\pi}{5} t) = 30 \sin (\dfrac{\pi}{50} t)\nonumber\]
The resulting graph is shown here.
Exercise \(\PageIndex{4}\)
A wheel of radius 4 is rolled around the outside of a circle of radius 7. Find a parametric equation for the position of a point on the boundary of the smaller wheel. This shape is called an epicycloid.
- Answer
-
The center of the small wheel rotates in circle with radius 7 + 4 = 11.
Since the circumference of the small circle is \(8\pi\) and the circumference of the large circle is \(22\pi\), in the time it takes to roll around the large circle, the small circle will have rotated \(\dfrac{22\pi}{8\pi} = \dfrac{11}{4}\) rotations. We use this as the stretch factor. The position of a point on the small circle will be the combination of the position of the center of the small wheel around the center of the large wheel, and the position of the point around the small wheel:
\[x(t) = 11 \cos(t) - 4\cos(\dfrac{11}{4} t)\nonumber\]
\[y(t) = 11\sin(t) - 4\sin(\dfrac{11}{4}t)\nonumber\]
Important Topics of This Section
- Parametric equations
- Graphing \(x(t)\), \(y(t)\) and the corresponding \(x-y\) graph Sketching graphs and building a table of values
- Converting parametric to Cartesian
- Converting Cartesian to parametric (parameterizing curves)


