Skip to main content
Mathematics LibreTexts

8.5.1: Dot Product (Exercise)

  1. Last updated
  2. Save as PDF
  • Page ID
    22246

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    section 8.5 exercises

    Two vectors are described by their magnitude and direction in standard position. Find the dot product of the vectors.

    1. Magnitude: 6, Direction: \(45^{\circ}\); Magnitude: 10, Direction: \(120^{\circ}\)

    2. Magnitude: 8, Direction: \(220^{\circ}\); Magnitude: 7, Direction: \(305^{\circ}\)

    Find the dot product of each pair of vectors.

    3. \(\langle 0, 4 \rangle; \langle -3, 0 \rangle\)

    4. \(\langle 6, 5 \rangle; \langle 3, 7 \rangle\)

    5. \(\langle -2, 1 \rangle; \langle -10, 13 \rangle\)

    6. \(\langle 2, -5 \rangle; \langle 8, -4 \rangle\)

    Find the angle between the vectors

    7. \(\langle 0, 4 \rangle; \langle -3, 0 \rangle\)

    8. \(\langle 6, 5 \rangle; \langle 3, 7 \rangle\)

    9. \(\langle 2, 4 \rangle; \langle 1, -3 \rangle\)

    10. \(\langle -4, 1 \rangle; \langle 8, -2 \rangle\)

    11. \(\langle 4, 2 \rangle; \langle 8, 4 \rangle\)

    12. \(\langle 5, 3 \rangle; \langle -6, 10 \rangle\)

    13. Find a value for \(k\) so that \(\langle 2, 7 \rangle\) and \(\langle k, 4 \rangle\) will be orthogonal.

    14. Find a value for \(k\) so that \(\langle -3, 5 \rangle\) and \(\langle 2, k \rangle\) will be orthogonal.

    15. Find the magnitude of the projection of \(\langle 8, -4 \rangle\) onto \(\langle 1, -3 \rangle\).

    16. Find the magnitude of the projection of \(\langle 2, 7 \rangle\) onto \(\langle 4, 5 \rangle\).

    17. Find the projection of \(\langle -6, 10 \rangle\) onto \(\langle 1, -3 \rangle\).

    18. Find the projection of \(\langle 0, 4 \rangle\) onto \(\langle 3, 7 \rangle\).

    19. A scientist needs to determine the angle of reflection when a laser hits a mirror. The picture shows the vector representing the laser beam, and a vector that is orthogonal to the mirror. Find the acute angle between these, the angle of reflection.

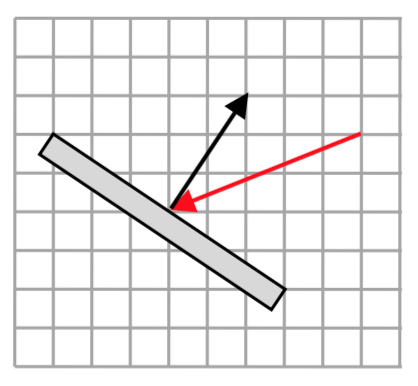
    屏幕快照 2019-07-22 下午3.53.59.png

    20. A triangle has coordinates at \(A\): (1,4), \(B\): (2,7), and \(C\): (4,2). Find the angle at point \(B\).

    21. A boat is trapped behind a log lying parallel to the dock. It only requires 10 pounds of force to pull th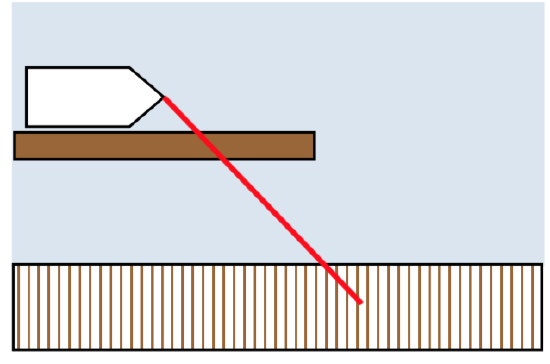屏幕快照 2019-07-22 下午3.55.14.pnge boat directly towards you, but because of the log, you'll have to pull at a \(45^{\circ}\) angle. How much force will you have to pull with? (We're going to assume that the log is very slimy and doesn't contribute any additional resistance.)

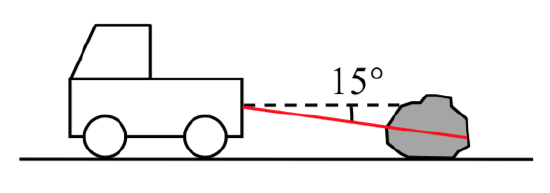
    22. A large boulder needs to be dragged to a new position. If pulled directly horizontally, the boulder would require 400 pounds of pulling force to move. We need to pull the boulder using a rope tied to the back of a large truck, forming a \(15^{\circ}\) angle from the ground. How much force will the truck need to pull with?

    屏幕快照 2019-07-22 下午3.56.36.png

    23. Find the work done against gravity by pushing a 20 pound cart 10 feet up a ramp that is \(10^{\circ}\) above horizontal. Assume there is no friction, so the only force is 20 pounds downwards due to gravity.

    24. Find the work done against gravity by pushing a 30 pound cart 15 feet up a ramp that is \(8^{\circ}\) above horizontal. Assume there is no friction, so the only force is 30 pounds downwards due to gravity.

    25. An object is pulled to the top of a 40 foot ramp that forms a \(10^{\circ}\) angle with the ground. It is pulled by rope exerting a force of 120 pounds at a \(35^{\circ}\) angle relative to the ground. Find the work done.

    26. An object is pulled to the top of a 30 foot ramp that forms a \(20^{\circ}\) angle with the ground. It is pulled by rope exerting a force of 80 pounds at a \(30^{\circ}\) angle relative to the ground. Find the work done.

    Answer

    1. \(6 \cdot 10 \cdot \cos(75^{\circ}) = 15.529\)

    3. (0)(-3) + (4)(0) = 0

    5. (-2)(-10) + (1)(13) = 33\)

    7. \(\cos^{-1} (\dfrac{0}{\sqrt{4}\sqrt{3}}) = 90^{\circ}\)

    9. \(\cos^(-1)(\dfrac{(2)(1) + (4)(-3)}{\sqrt{2^2 + 4^2}\sqrt{1^2 + (-3)^2}}) = 135^{\circ}\)

    11. \(\cos^(-1)(\dfrac{(4)(8) + (2)(4)}{\sqrt{4^2 + 8^2}\sqrt{2^2 + 4^2}}) = 0^{\circ}\)

    13. \((2)(k) + (7)(4) = 0, k = -14\)

    15. \(\dfrac{(8)(1) + (-4)(-3)}{\sqrt{1^2 + (-3)^2}} = 6.325\)

    17. \((\dfrac{(-6)(1) + (10)(-3)}{\sqrt{1^2 + (-3)^2}}^2) \langle 1, -3 \rangle = \langle -3.6, 10.8 \rangle\)

    19. The vectors are \(\langle 2, 3 \rangle\) and \(\langle -5, -2 \rangle\). The acute angle between the vectors is \(34.509^{\circ}\)

    21. 14.142 pounds

    23. \(\langle 10\cos(10^{\circ}), 10\sin(10^{\circ}) \rangle \cdot \langle 0, -20 \rangle\), so 34.7296 ft-lbs

    25. \(40 \cdot 120 \cdot \cos(25^{\circ}) = 4350.277\) ft-lbs

    This page titled 8.5.1: Dot Product (Exercise) is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by David Lippman & Melonie Rasmussen (The OpenTextBookStore) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.