2.4: Fitting Linear Models to Data
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the real world, rarely do things follow trends perfectly. When we expect the trend to behave linearly, or when inspection suggests the trend is behaving linearly, it is often desirable to find an equation to approximate the data. Finding an equation to approximate the data helps us understand the behavior of the data and allows us to use the linear model to make predictions about the data, inside and outside of the data range.
Example 2.4.1
The table below shows the number of cricket chirps in 15 seconds, and the air temperature, in degrees Fahrenheit (Selected data from classic.globe.gov/fsl/scientistsblog/2007/10/. Retrieved Aug 3, 2010). Plot this data, and determine whether the data appears to be linearly related.
| chirps | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| Temp | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
Solution
Plotting this data, it appears there may be a trend, and that the trend appears roughly linear, though certainly not perfectly so.
The simplest way to find an equation to approximate this data is to try to “eyeball” a line that seems to fit the data pretty well, then find an equation for that line based on the slope and intercept.
You can see from the trend in the data that the number of chirps increases as the temperature increases. As you consider a function for this data you should know that you are looking at an increasing function or a function with a positive slope.
flashback
- What descriptive variables would you choose to represent Temperature & Chirps?
- Which variable is the independent variable and which is the dependent variable?
- Based on this data and the graph, what is a reasonable domain & range?
- Based on the data alone, is this function one-to-one, explain?
- Answer
-
1. a. T = Temperature, C = Chirps (answers may vary)
b. Independent (Chirps) , Dependent (Temperature)
c. Reasonable Domain (18.5, 44) , Reasonable Range (52, 80.5) (answers may vary)
d. NO, it is not one-to-one, there are two different output values for 35 chirps.
Example 2.4.2
Using the table of values from the previous example, find a linear function that fits the data by “eyeballing” a line that seems to fit.
Solution
 On a graph, we could try sketching in a line. Note the scale on the axes have been adjusted to start at zero to include the vertical axis and vertical intercept in the graph.
On a graph, we could try sketching in a line. Note the scale on the axes have been adjusted to start at zero to include the vertical axis and vertical intercept in the graph.
Using the starting and ending points of our “hand drawn” line, points (0, 30) and (50, 90), this graph has a slope of m=6050=1.2 and a vertical intercept at 30, giving an equation of
T(c)=30+1.2c
where c is the number of chirps in 15 seconds, and T(c) is the temperature in degrees Fahrenheit.
This linear equation can then be used to approximate the solution to various questions we might ask about the trend. While the data does not perfectly fall on the linear equation, the equation is our best guess as to how the relationship will behave outside of the values we have data for. There is a difference, though, between making predictions inside the domain and range of values we have data for, and outside that domain and range.
Definition: Interpolation and Extrapolation
Interpolation: When we predict a value inside the domain and range of the data
Extrapolation: When we predict a value outside the domain and range of the data
For the Temperature as a function of chirps in our hand drawn model above,
- Interpolation would occur if we used our model to predict temperature when the values for chirps are between 18.5 and 44.
- Extrapolation would occur if we used our model to predict temperature when the values for chirps are less than 18.5 or greater than 44.
Example 2.4.3
- Would predicting the temperature when crickets are chirping 30 times in 15 seconds be interpolation or extrapolation? Make the prediction, and discuss if it is reasonable.
- Would predicting the number of chirps crickets will make at 40 degrees be interpolation or extrapolation? Make the prediction, and discuss if it is reasonable.
Solution
With our cricket data, our number of chirps in the data provided varied from 18.5 to 44. A prediction at 30 chirps per 15 seconds is inside the domain of our data, so would be interpolation. Using our model:
T(3)=30+1.2(30)=66 degrees
Based on the data we have, this value seems reasonable.
The temperature values varied from 52 to 80.5. Predicting the number of chirps at 40 degrees is extrapolation since 40 is outside the range of our data. Using our model:
40=30+1.2c10=1.2cc≈8.33
Our model predicts the crickets would chirp 8.33 times in 15 seconds. While this might be possible, we have no reason to believe our model is valid outside the domain and range. In fact, generally crickets stop chirping altogether below around 50 degrees.
When our model no longer applies after some point, it is sometimes called model breakdown.
Exercise 2.4.1
What temperature would you predict if you counted 20 chirps in 15 seconds?
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.
Fitting Lines with Technology
While eyeballing a line works reasonably well, there are statistical techniques for fitting a line to data that minimize the differences between the line and data values (Technically, the method minimizes the sum of the squared differences in the vertical direction between the line and the data values.). This technique is called least-square regression, and can be computed by many graphing calculators, spreadsheet software like Excel or Google Docs, statistical software, and many web-based calculators(For example, http://www.shodor.org/unchem/math/lls/leastsq.html).
Example 2.4.4
Find the least-squares regression line using the cricket chirp data from above.
Solution
Using the cricket chirp data from earlier, with technology we obtain the equation: 
T(c)=30.281+1.143c
Notice that this line is quite similar to the equation we “eyeballed”, but should fit the data better. Notice also that using this equation would change our prediction for the temperature when hearing 30 chirps in 15 seconds from 66 degrees to:
T(30)=30.281+1.143(30)=64.571≈64.6 degrees
Most calculators and computer software will also provide you with the correlation coefficient, a measure of how closely the line fits the data.
Definition: correlation coefficient
The correlation coefficient is a value, r, between -1 and 1.
r>0 suggests a positive (increasing) relationship
r<0 suggests a negative (decreasing) relationship
The closer the value is to 0, the more scattered the data
The closer the value is to 1 or -1, the less scattered the data is
The correlation coefficient provides an easy way to get some idea of how close to a line the data falls.
We should only compute the correlation coefficient for data that follows a linear pattern; if the data exhibits a non-linear pattern, the correlation coefficient is meaningless. To get a sense for the relationship between the value of r and the graph of the data, here are some large data sets with their correlation coefficients:
Examples of Correlation Coefficient Values
(http://en.Wikipedia.org/wiki/File:Co...n_examples.png)
Example 2.4.5
Calculate the correlation coefficient for our cricket data.
Solution
Because the data appears to follow a linear pattern, we can use technology to calculate r = 0.9509. Since this value is very close to 1, it suggests a strong increasing linear relationship.
Example 2.4.6
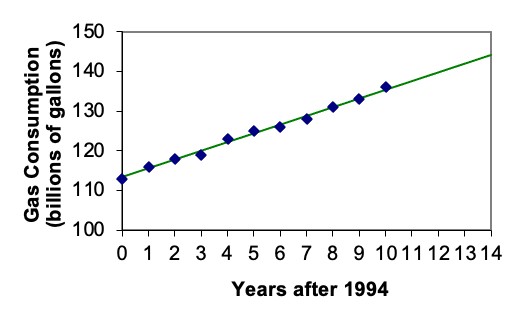
Gasoline consumption in the US has been increasing steadily. Consumption data from 1994 to 2004 is shown below.(www.bts.gov/publications/nati...ble_04_10.html) Determine if the trend is linear, and if so, find a model for the data. Use the model to predict the consumption in 2008.
| Year | '94 | '95 | '96 | '97 | '98 | '99 | '00 | '01 | '02 | '03 | '04 |
| Consumption (billions of gallons) | 113 | 116 | 118 | 119 | 123 | 125 | 126 | 128 | 131 | 133 | 136 |
Solution
To make things simpler, a new input variable is introduced, t, representing years since 1994.
Using technology, the correlation coefficient was calculated to be 0.9965, suggesting a very strong increasing linear trend.
The least-squares regression equation is:
C(t)=113.318+2.209t
Using this to predict consumption in 2008 (t = 14),
C(14)=113.318+2.209(14)=144.244 billions of gallons
The model predicts 144.244 billion gallons of gasoline will be consumed in 2008.
Exercise 2.4.2
Use the model created by technology in example 6 to predict the gas consumption in 2011. Is this an interpolation or an extrapolation?
- Answer
-
1. 54 degrees Fahrenheit
2. 150.871 billion gallons; extrapolation
Important Topics of this Section
- Fitting linear models to data by hand
- Fitting linear models to data using technology
- Interpolation
- Extrapolation
- Correlation coefficient


