2.5: Absolute Value Functions
- Page ID
- 13838
So far in this chapter we have been studying the behavior of linear functions. The Absolute Value Function is a piecewise-defined function made up of two linear functions. The name, Absolute Value Function, should be familiar to you from Section 1.2. In its basic form\(f(x)=\left|x\right|\) it is one of our toolkit functions.
Definition: Absolute Value Function
The absolute value function can be defined as
\[f(x)=\left|x\right|=\left\{\begin{array}{ccc} {x} & {if} & {x\ge 0} \\ {-x} & {if} & {x<0} \end{array}\right.\]
The absolute value function is commonly used to determine the distance between two numbers on the number line. Given two values a and b, then \(\left|a-b\right|\) will give the distance, a positive quantity, between these values, regardless of which value is larger.
Example \(\PageIndex{1}\)
Describe all values, \(x\), within a distance of 4 from the number 5.
Solution
We want the distance between \(x\) and 5 to be less than or equal to 4. The distance can be represented using the absolute value, giving the expression
\[\left|x-5\right|\le 4\nonumber \]
Example \(\PageIndex{2}\)
A 2010 poll reported 78% of Americans believe that people who are gay should be able to serve in the US military, with a reported margin of error of 3% (http://www.pollingreport.com/civil.htm, retrieved August 4, 2010). The margin of error tells us how far off the actual value could be from the survey value (Technically, margin of error usually means that the surveyors are 95% confident that actual value falls within this range.). Express the set of possible values using absolute values.
Solution
Since we want the size of the difference between the actual percentage, \(p\), and the reported percentage to be less than 3%,
\[\left|p-78\right|\le 3\nonumber \]
Exercise \(\PageIndex{1}\)
Students who score within 20 points of 80 will pass the test. Write this as a distance from 80 using the absolute value notation.
- Answer
-
Using the variable p, for passing, \(\left|p-80\right|\le 20\)
Important Features
The most significant feature of the absolute value graphAbsolute Value Functions:Graphing is the corner point where the graph changes direction. When finding the equation for a transformed absolute value function, this point is very helpful for determining the horizontal and vertical shifts.
Example \(\PageIndex{3}\)
Write an equation for the function graphed.
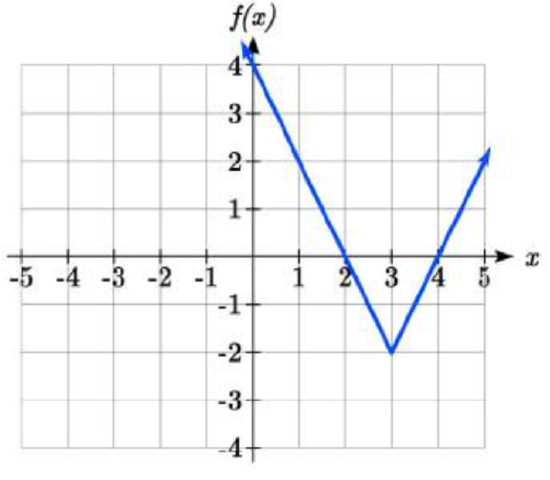
Solution
The basic absolute value function changes direction at the origin, so this graph has been shifted to the right 3 and down 2 from the basic toolkit function.
We might also notice that the graph appears stretched, since the linear portions have slopes of 2 and -2. From this information we could write the write the equation in two ways:
\(f(x)=2\left|x-3\right|-2\), treating the stretch as a vertical stretch
\(f(x)=\left|2(x-3)\right|-2\), treating the stretch as a horizontal compression
Note that these equations are algebraically equivalent – the stretch for an absolute value function can be written interchangeably as a vertical or horizontal stretch/compression.
If you had not been able to determine the stretch based on the slopes of the lines, you can solve for the stretch factor by putting in a known pair of values for x and f(x)
\[f(x)=a\left|x-3\right|-2\nonumber \] Now substituting in the point (1, 2)
\[\begin{array}{l} {2=a\left|1-3\right|-2} \\ {4=2a} \\ {a=2} \end{array}\nonumber \]
Exercise \(\PageIndex{2}\)
Given the description of the transformed absolute value function write the equation. The absolute value function is horizontally shifted left 2 units, is vertically flipped, and vertically shifted up 3 units.
- Answer
-
\[f(x)=-\left|x+2\right|+3\nonumber \]
The graph of an absolute value function will have a vertical intercept when the input is zero. The graph may or may not have horizontal intercepts, depending on how the graph has been shifted and reflected. It is possible for the absolute value function to have zero, one, or two horizontal intercepts.
Zero horizontal intercepts One Two One Two
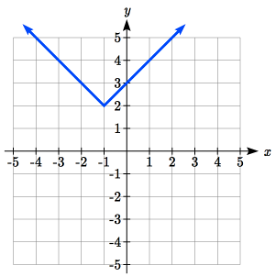
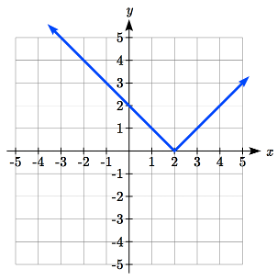
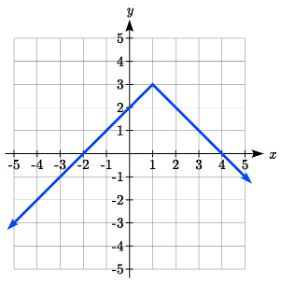
To find the horizontal intercepts, we will need to solve an equation involving an absolute value.
Notice that the absolute value function is not one-to-one, so typically inverses of absolute value functions are not discussed.
Solving Absolute Value Equations
Absolute Value Functions:Solving
To solve an equation like \(8=\left|2x-6\right|\), we can notice that the absolute value will be equal to eight if the quantity inside the absolute value were 8 or -8. This leads to two different equations we can solve independently:
\[2x - 6 = 8\text{ or }2x - 6 = -8\nonumber \]
\[2x = 14\quad 2x = -2\nonumber\]
\[x = 7\quad x = -1\nonumber\]
solutions to absolute value equations
An equation of the form \(\left|A\right|=B\), with \(B\ge 0\), will have solutions when
\[A=B\text{ or }A=-B\nonumber\]
Example \(\PageIndex{4}\)
Find the horizontal intercepts of the graph of \(f(x)=\left|4x+1\right|-7\)
Solution
The horizontal intercepts will occur when \(f(x)=0\). Solving,
\[0=|4x+1|-7\nonumber \] Isolate the absolute value on one side of the equation
\[7=|4x+1|\nonumber \] Now we can break this into two separate equations:
\[7 = 4x + 1\quad -7 = 4x + 1\nonumber\]
\[6 = 4x\text{ or }-8 = 4x\nonumber\]
\[x = \dfrac{6}{4} = \dfrac{3}{2}\quad x = \dfrac{-8}{4} = -2\nonumber\]
The graph has two horizontal intercepts, at \(x=\dfrac{3}{2}\) and \(x = -2\)
Example \(\PageIndex{5}\)
Solve \(1=4\left|x-2\right|+2\)
Solution
Isolating the absolute value on one side the equation,
\[1=4\left|x-2\right|+2\nonumber\]
\[-1=4\left|x-2\right|\nonumber\]
\[-\dfrac{1}{4} =\left|x-2\right|\nonumber\]
At this point, we notice that this equation has no solutions – the absolute value always returns a positive value, so it is impossible for the absolute value to equal a negative value.
Exercise \(\PageIndex{3}\)
Find the horizontal & vertical intercepts for the function\(f(x)=-\left|x+2\right|+3\)
- Answer
-
\(f(0) = 1\), so the vertical intercept is at (0,1).
\(f(x)= 0\) when
\[-\left|x+2\right|+3=0\nonumber \]
\[\left|x+2\right|=3\nonumber \]
\[x+2=3\text{ or }x+2=-3\nonumber\]
\[x = 1\text{ or }x = -5\nonumber \] so the horizontal intercepts are at (-5,0) & (1,0)
Solving Absolute Value Inequalities
Absolute Value Functions:Solving Inequalities
When absolute value inequalities are written to describe a set of values, like the inequality \(\left|x-5\right|\le 4\) we wrote earlier, it is sometimes desirable to express this set of values without the absolute value, either using inequalities, or using interval notation.
We will explore two approaches to solving absolute value inequalities:
- Using the graph
- Using test values
Example \(\PageIndex{6}\)
Solve \(\left|x-5\right|\le 4\)
Solution
With both approaches, we will need to know first where the corresponding equality is true. In this case, we first will find where \(\left|x-5\right|=4\). We do this because the absolute value is a nice friendly function with no breaks, so the only way the function values can switch from being less than 4 to being greater than 4 is by passing through where the values equal 4. Solve \(\left|x-5\right|=4\),
\[\begin{array}{l} {x-5=4} \\ {x=9} \end{array}\text{ or } \begin{array}{l} {x-5=-4} \\ {x=1} \end{array}\nonumber \]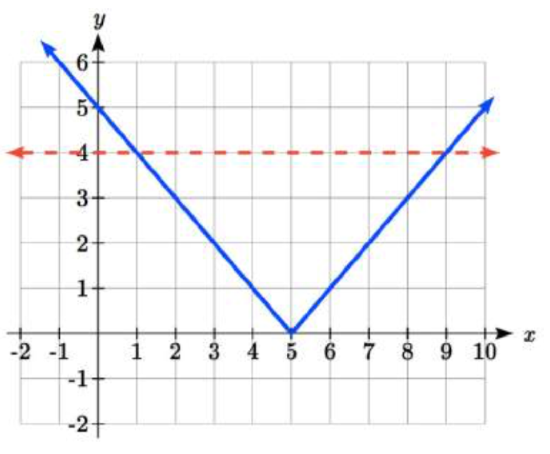
To use a graph, we can sketch the function \(f(x)=\left|x-5\right|\). To help us see where the outputs are 4, the line \(g(x)=4\) could also be sketched.
On the graph, we can see that indeed the output values of the absolute value are equal to 4 at \(x = 1\) and \(x = 9\). Based on the shape of the graph, we can determine the absolute value is less than or equal to 4 between these two points, when \(1 \le x \le 9\). In interval notation, this would be the interval [1,9].
As an alternative to graphing, after determining that the absolute value is equal to 4 at \(x = 1\) and \(x = 9\), we know the graph can only change from being less than 4 to greater than 4 at these values. This divides the number line up into three intervals: \(x < 1\), \(1 < x < 9\), and \(x > 9\). To determine when the function is less than 4, we could pick a value in each interval and see if the output is less than or greater than 4.
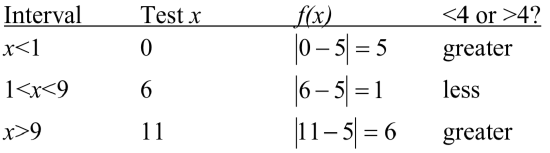
Since \(1 \le x \le 9\) is the only interval in which the output at the test value is less than 4, we can conclude the solution to \(\left|x-5\right| \le 4\) is \(1 \le x \le 9\).
Example \(\PageIndex{7}\)
Given the function \(f(x)=-\dfrac{1}{2} \left|4x-5\right|+3\), determine for what \(x\) values the function values are negative.
Solution
We are trying to determine where \(f(x) < 0\), which is when \(-\dfrac{1}{2} \left|4x-5\right|+3<0\). We begin by isolating the absolute value:
\[-\dfrac{1}{2} \left|4x-5\right|<-3\nonumber\] when we multiply both sides by -2, it reverses the inequality
\[\left|4x-5\right|>6\nonumber \]
Next we solve for the equality \(\left|4x-5\right|=6\)
\[\begin{array}{l} {4x-5=6} \\ {4x=11} \\ {x=\dfrac{11}{4} } \end{array}\text{ or }\begin{array}{l} {4x-5=-6} \\ {4x=-1} \\ {x=\dfrac{-1}{4} } \end{array}\nonumber \]
We can now either pick test values or sketch a graph of the function to determine on which intervals the original function value are negative. Notice that it is not even really important exactly what the graph looks like, as long as we know that it crosses the horizontal axis at \(x=\dfrac{-1}{4}\) and \(x=\dfrac{11}{4}\), and that the graph has been reflected vertically.
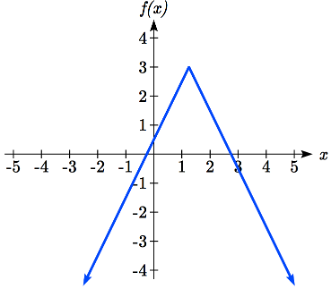
From the graph of the function, we can see the function values are negative to the left of the first horizontal intercept at \(x=\dfrac{-1}{4}\), and negative to the right of the second intercept at \(x=\dfrac{11}{4}\). This gives us the solution to the inequality:
\[x<\dfrac{-1}{4} \quad \text{or}\quad x>\dfrac{11}{4}\nonumber \]
In interval notation, this would be \(\left(-\infty ,\dfrac{-1}{4} \right)\bigcup \left(\dfrac{11}{4} ,\infty \right)\)
Exercise \(\PageIndex{4}\)
Solve\(-2\left|k-4\right|\le -6\)
- Answer
-
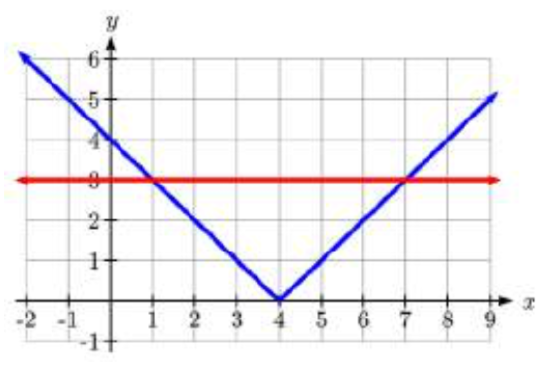 \[-2\left|k-4\right|\le -6\nonumber \]
\[-2\left|k-4\right|\le -6\nonumber \]\[\left|k-4\right|\ge 3\nonumber \]
Solving the equality \(\left|k-4\right|=3\), k – 4 = 3 or k – 4 = –3, so k = 1 or k = 7.Using a graph or test values, we can determine the intervals that satisfy the inequality are \(k\le 1\) or \(k\ge 7\); in interval notation this would be \(\left(-\infty ,1\right]\cup \left[7,\infty \right)\)
Important Topics of this Section
- The properties of the absolute value function
- Solving absolute value equations
- Finding intercepts
- Solving absolute value inequalities


