3.2E: Quadratic Functions (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
section 3.2 exercise
Write an equation for the quadratic function graphed.
1. 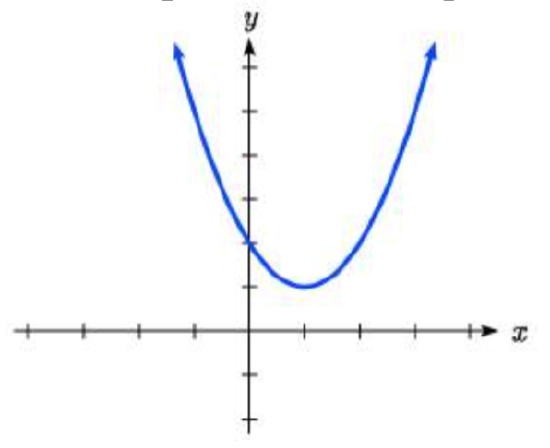 2.
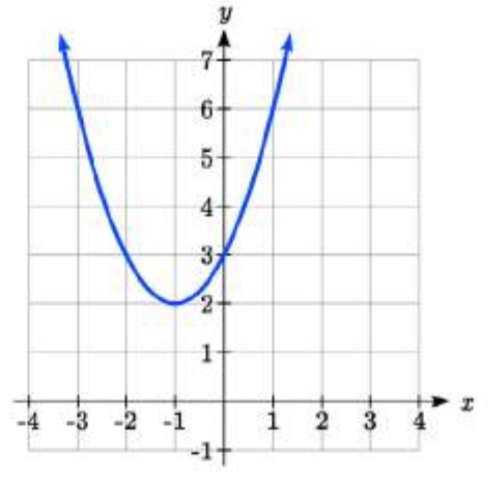
2. 
3. 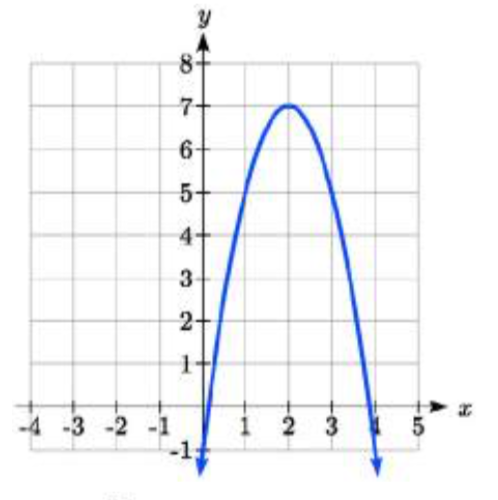 4.
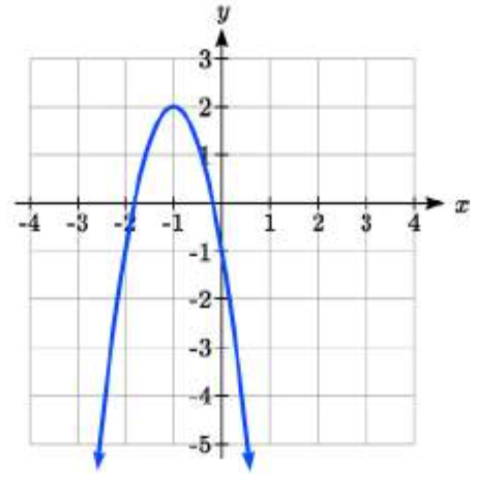
4. 
5. 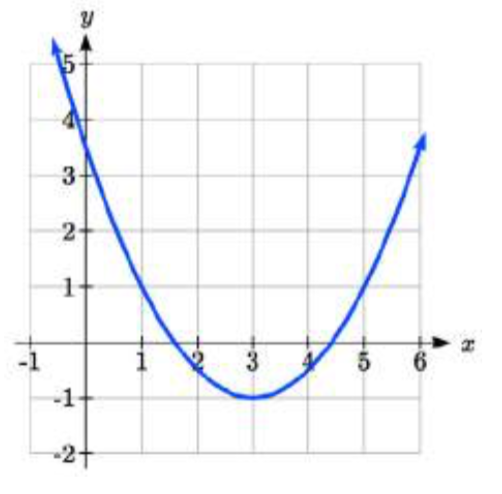 6.
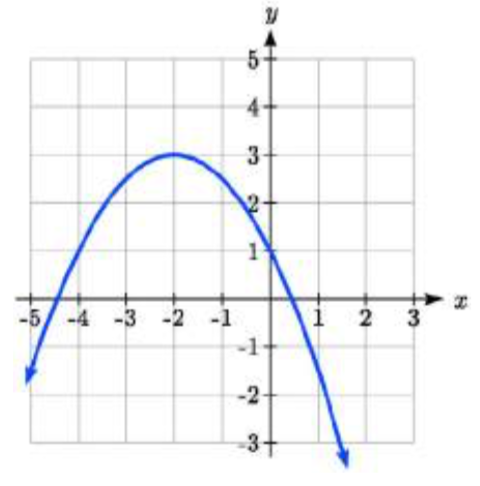
6. 
For each of the follow quadratic functions, find a) the vertex, b) the vertical intercept, and c) the horizontal intercepts.
7. y(x)=2x2+10x+12
8. z(p)=3x2+6x−9
9. f(x)=2x2−10x+4
10. g(x)=−2x2−14x+12
11. h(t)=−4t2+6t−1
12. k(t)=2x2+4x−15
Rewrite the quadratic function into vertex form.
13. (x)=x2−12x+32
14. g(x)=x2+2x−3
15. h(x)=2x2+8x−10
16. k(x)=3x2−6x−9
17. Find the values of b and c so f(x)=−8x2+bx+c has vertex 2,−7)
18. Find the values of b and c so f(x)=6x2+bx+c has vertex (7,−9)
Write an equation for a quadratic with the given features
19. x-intercepts (-3, 0) and (1, 0), and y intercept (0, 2)
20. x-intercepts (2, 0) and (-5, 0), and y intercept (0, 3)
21. x-intercepts (2, 0) and (5, 0), and y intercept (0, 6)
22. x-intercepts (1, 0) and (3, 0), and y intercept (0, 4)
23. Vertex at (4, 0), and y intercept (0, -4)
24. Vertex at (5, 6), and y intercept (0, -1)
25. Vertex at (-3, 2), and passing through (3, -2)
26. Vertex at (1, -3), and passing through (-2, 3)
27. A rocket is launched in the air. Its height, in meters above sea level, as a function of time, in seconds, is given by h(t)=−4.9t2+229t+234.
a. From what height was the rocket launched?
b. How high above sea level does the rocket reach its peak?
c. Assuming the rocket will splash down in the ocean, at what time does splashdown occur?
28. A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by h(t)=−4.9t2+24t+8.
a. From what height was the ball thrown?
b. How high above ground does the ball reach its peak?
c. When does the ball hit the ground?
29. The height of a ball thrown in the air is given by h(x)=−112x2+6x+3, where x is the horizontal distance in feet from the point at which the ball is thrown.
a. How high is the ball when it was thrown?
b. What is the maximum height of the ball?
c. How far from the thrower does the ball strike the ground?
30. A javelin is thrown in the air. Its height is given by h(x)=−120x2+8x+6, where x is the horizontal distance in feet from the point at which the javelin is thrown.
a. How high is the javelin when it was thrown?
b. What is the maximum height of the javelin?
c. How far from the thrower does the javelin strike the ground?
31. A box with a square base and no top is to be made from a square piece of cardboard by cutting 6 in. squares out of each corner and folding up the sides. The box needs to hold 1000 in3. How big a piece of cardboard is needed?
32. A box with a square base and no top is to be made from a square piece of cardboard by cutting 4 in. squares out of each corner and folding up the sides. The box needs to hold 2700 in3. How big a piece of cardboard is needed?
33. 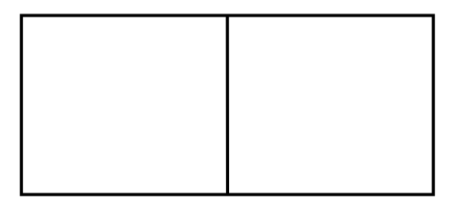 A farmer wishes to enclose two pens with fencing, as shown. If the farmer has 500 feet of fencing to work with, what dimensions will maximize the area enclosed?
A farmer wishes to enclose two pens with fencing, as shown. If the farmer has 500 feet of fencing to work with, what dimensions will maximize the area enclosed?
34.  A farmer wishes to enclose three pens with fencing, as shown. If the farmer has 700 feet of fencing to work with, what dimensions will maximize the area enclosed?
A farmer wishes to enclose three pens with fencing, as shown. If the farmer has 700 feet of fencing to work with, what dimensions will maximize the area enclosed?
35. You have a wire that is 56 cm long. You wish to cut it into two pieces. One piece will be bent into the shape of a square. The other piece will be bent into the shape of a circle. Let A represent the total area enclosed by the square and the circle. What is the circumference of the circle when A is a minimum?
36. You have a wire that is 71 cm long. You wish to cut it into two pieces. One piece will be bent into the shape of a right triangle with legs of equal length. The other piece will be bent into the shape of a circle. Let A represent the total area enclosed by the triangle and the circle. What is the circumference of the circle when A is a minimum?
37. A soccer stadium holds 62,000 spectators. With a ticket price of $11, the average attendance has been 26,000. When the price dropped to $9, the average attendance rose to 31,000. Assuming that attendance is linearly related to ticket price, what ticket price would maximize revenue?
38. A farmer finds that if she plants 75 trees per acre, each tree will yield 20 bushels of fruit. She estimates that for each additional tree planted per acre, the yield of each tree will decrease by 3 bushels. How many trees should she plant per acre to maximize her harvest?
39. 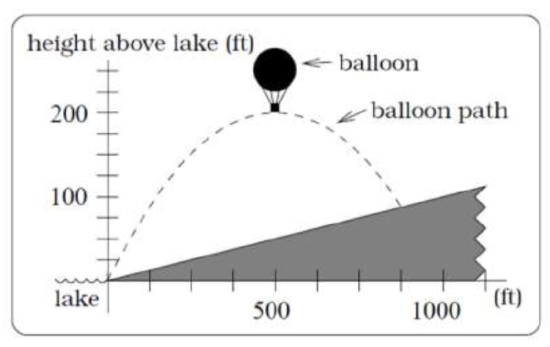 A hot air balloon takes off from the edge of a mountain lake. Impose a coordinate system as pictured and assume that the path of the balloon follows the graph of f(x)=−22500x2+45x. The land rises at a constant incline from the lake at the rate of 2 vertical feet for each 20 horizontal feet. [UW]
A hot air balloon takes off from the edge of a mountain lake. Impose a coordinate system as pictured and assume that the path of the balloon follows the graph of f(x)=−22500x2+45x. The land rises at a constant incline from the lake at the rate of 2 vertical feet for each 20 horizontal feet. [UW]
a. What is the maximum height of the balloon above water level?
b. What is the maximum height of the balloon above ground level?
c. Where does the balloon land on the ground?
d. Where is the balloon 50 feet above the ground?
40. 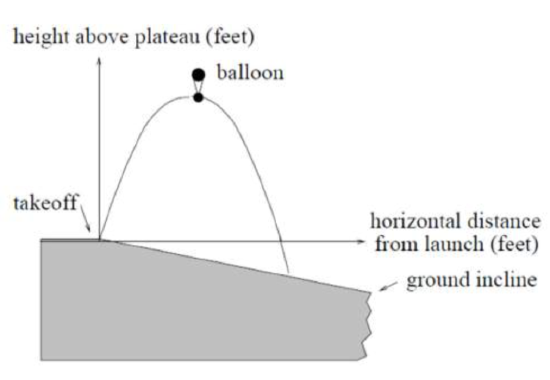 A hot air balloon takes off from the edge of a plateau. Impose a coordinate system as pictured below and assume that the path the balloon follows is the graph of the quadratic function f(x)=−42500x2+45x. The land drops at a constant incline from the plateau at the rate of 1 vertical foot for each 5 horizontal feet. [UW]
A hot air balloon takes off from the edge of a plateau. Impose a coordinate system as pictured below and assume that the path the balloon follows is the graph of the quadratic function f(x)=−42500x2+45x. The land drops at a constant incline from the plateau at the rate of 1 vertical foot for each 5 horizontal feet. [UW]
a. What is the maximum height of the balloon above plateau level?
b. What is the maximum height of the balloon above ground level?
c. Where does the balloon land on the ground?
d. Where is the balloon 50 feet above the ground?
- Answer
-
1. f(x)=(x−2)2−3
3. f(x)=−2(x−2)2+7
5. f(x)=12(x−3)2−1
Vertex Vertical Intercept Horizontal Intercepts 7. (-2.5, -0.5) (0, 12) (-2, 0). (-3, 0) 9. (2.5, -8.5) (0, 4) (0.438, 0). (4.562, 0) 11. (0.75, 1.25) (0, -1) (0.191, 0). (1.309, 0) 13. f(x)=(x−6)2−4
15. f(x=2(x+2)2−18
17. b=32 and c=−39
19. f(x)−−23(x+3)(x−1)
21. f(x)=35(x−2)(x−5)
23. f(x)=−14(x−4)2
25. f(x)=−19(x+3)2+2
27a. 234m
b. 2909.561 ft
c. 47.735 seconds29a. 3 ft
b. 111 ft
c. 72.497 ft31. 24.91 in by 24.91 in
33. 125 ft by 8313ft
35. 24.6344 cm
37. $10.70


