3.4: Factor Theorem and Remainder Theorem

In the last section, we limited ourselves to finding the intercepts, or zeros, of polynomials that factored simply, or we turned to technology. In this section, we will look at algebraic techniques for finding the zeros of polynomials like $h(t)=t^{3} +4t^{2} +t-6$.

Long Division

In the last section we saw that we could write a polynomial as a product of factors, each corresponding to a horizontal intercept. If we knew that $x = 2$ was an intercept of the polynomial $x^3 + 4x^2 - 5x - 14$, we might guess that the polynomial could be factored as $x^{3} +4x^{2} -5x-14=(x-2)$ (something). To find that "something," we can use polynomial division.

Example $\PageIndex{1}$

Divide $x^{3} +4x^{2} -5x-14$ by $x-2$.

Solution

Start by writing the problem out in long division form

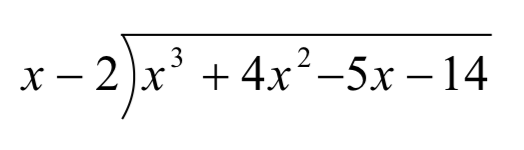
Now we divide the leading terms: $x^{3} \div x=x^{2}$. It is best to align it above the same-powered term in the dividend. Now, multiply that $x^{2}$ by $x-2$ and write the result below the dividend.

Again, divide the leading term of the remainder by the leading term of the divisor. $6x^{2} \div x=6x$. We add this to the result, multiply 6x by $x-2$, and subtract.

This tells us $x^{3} +4x^{2} -5x-14$ divided by $x-2$ is $x^{2} +6x+7$, with a remainder of zero. This also means that we can factor $x^{3} +4x^{2} -5x-14$ as $\left(x-2\right)\left(x^{2} +6x+7\right)$.

This gives us a way to find the intercepts of this polynomial.

Example $\PageIndex{2}$

Find the horizontal intercepts of $h(x)=x^{3} +4x^{2} -5x-14$.

Solution

To find the horizontal intercepts, we need to solve $h(x) = 0$. From the previous example, we know the function can be factored as $h(x)=\left(x-2\right)\left(x^{2} +6x+7\right)$.

$h(x)=\left(x-2\right)\left(x^{2} +6x+7\right)=0$ when $x = 2$ or when $x^{2} +6x+7=0$. This doesn’t factor nicely, but we could use the quadratic formula to find the remaining two zeros.

$$x=\dfrac{-6\pm \sqrt{6^{2} -4(1)(7)} }{2(1)} =-3\pm \sqrt{2} \nonumber$$

The horizontal intercepts will be at $(2,0)$, $\left(-3-\sqrt{2} ,0\right)$, and $\left(-3+\sqrt{2} ,0\right)$.

Exercise $\PageIndex{1}$

Divide $2x^{3} -7x+3$ by $x+3$ using long division.

Answer

The Factor and Remainder Theorems

When we divide a polynomial, $p(x)$ by some divisor polynomial $d(x)$, we will get a quotient polynomial $q(x)$ and possibly a remainder $r(x)$. In other words,

$$p(x)=d(x)q(x)+r(x)$$

Because of the division, the remainder will either be zero, or a polynomial of lower degree than d(x). Because of this, if we divide a polynomial by a term of the form $x-c$, then the remainder will be zero or a constant.

If $p(x)=(x-c)q(x)+r$, then $p(c)=(c-c)q(c)+r=0+r=r$, which establishes the Remainder Theorem.

The Remainder Theorem

If $p(x)$ is a polynomial of degree 1 or greater and c is a real number, then when p(x) is divided by $x-c$, the remainder is $p(c)$.

If $x-c$ is a factor of the polynomial $p$, then $p(x)=(x-c)q(x)$ for some polynomial $q$. Then $p(c)=(c-c)q(c)=0$, showing $c$ is a zero of the polynomial. This shouldn’t surprise us - we already knew that if the polynomial factors it reveals the roots.

If $p(c)=0$, then the remainder theorem tells us that if p is divided by $x-c$, then the remainder will be zero, which means $x-c$ is a factor of $p$.

the factor theorem

If $p(x)$ is a nonzero polynomial, then the real number $c$ is a zero of $p(x)$ if and only if $x-c$ is a factor of $p(x)$.

Synthetic Division

Since dividing by $x-c$ is a way to check if a number is a zero of the polynomial, it would be nice to have a faster way to divide by $x-c$ than having to use long division every time. Happily, quicker ways have been discovered.

Let’s look back at the long division we did in Example 1 and try to streamline it. First, let’s change all the subtractions into additions by distributing through the negatives.

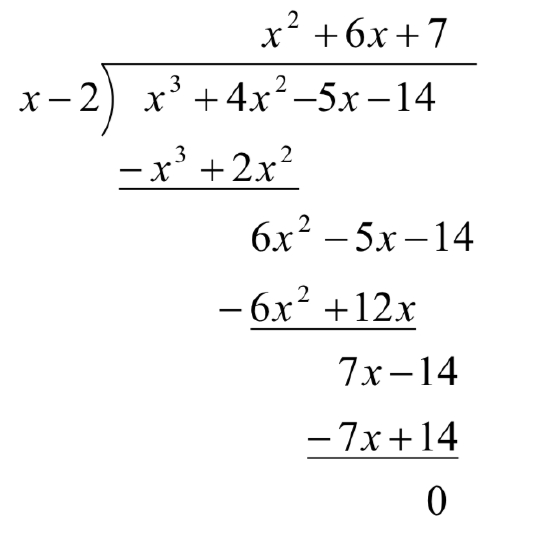
Next, observe that the terms $-x^{3}$, $-6x^{2}$, and $-7x$ are the exact opposite of the terms above them. The algorithm we use ensures this is always the case, so we can omit them without losing any information. Also note that the terms we ‘bring down’ (namely the $\mathrm{-}$5x and $\mathrm{-}$14) aren’t really necessary to recopy, so we omit them, too.

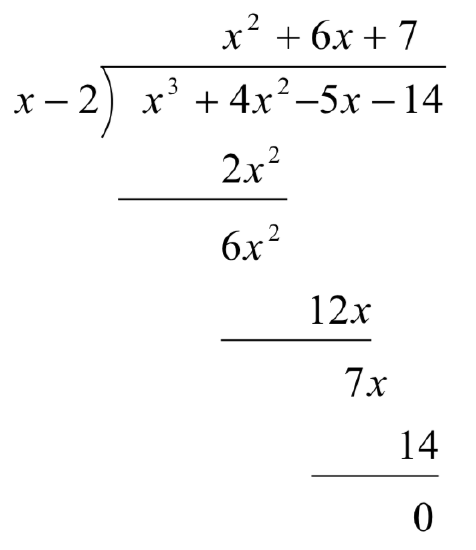
Now, let’s move things up a bit and, for reasons which will become clear in a moment, copy the $x^{3}$ into the last row.

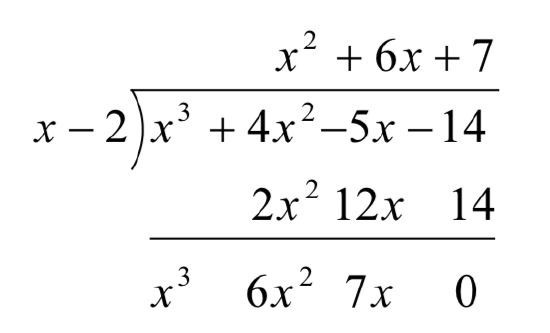
Note that by arranging things in this manner, each term in the last row is obtained by adding the two terms above it. Notice also that the quotient polynomial can be obtained by dividing each of the first three terms in the last row by $x$ and adding the results. If you take the time to work back through the original division problem, you will find that this is exactly the way we determined the quotient polynomial.

This means that we no longer need to write the quotient polynomial down, nor the $x$ in the divisor, to determine our answer.

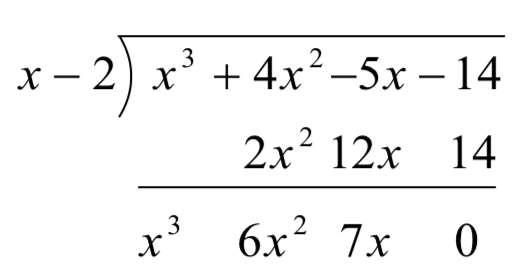
We’ve streamlined things quite a bit so far, but we can still do more. Let’s take a moment to remind ourselves where the $2x^{2}$, $12x$ and 14 came from in the second row. Each of these terms was obtained by multiplying the terms in the quotient, $x^{2}$, 6x and 7, respectively, by the -2 in $x - 2$, then by -1 when we changed the subtraction to addition. Multiplying by -2 then by -1 is the same as multiplying by 2, so we replace the -2 in the divisor by 2. Furthermore, the coefficients of the quotient polynomial match the coefficients of the first three terms in the last row, so we now take the plunge and write only the coefficients of the terms to get

We have constructed a synthetic division tableau for this polynomial division problem. Let’s re-work our division problem using this tableau to see how it greatly streamlines the division process. To divide $x^{3} +4x^{2} -5x-14$ by $x-2$, we write 2 in the place of the divisor and the coefficients of $x^{3} +4x^{2} -5x-14$in for the dividend. Then "bring down" the first coefficient of the dividend.

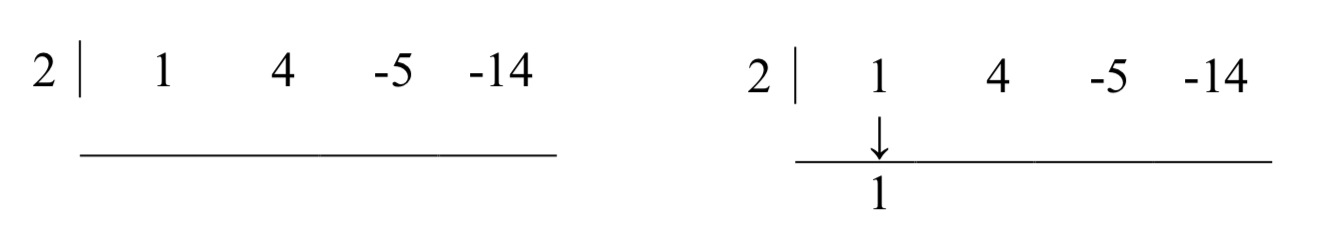
Next, take the 2 from the divisor and multiply by the 1 that was "brought down" to get 2. Write this underneath the 4, then add to get 6.

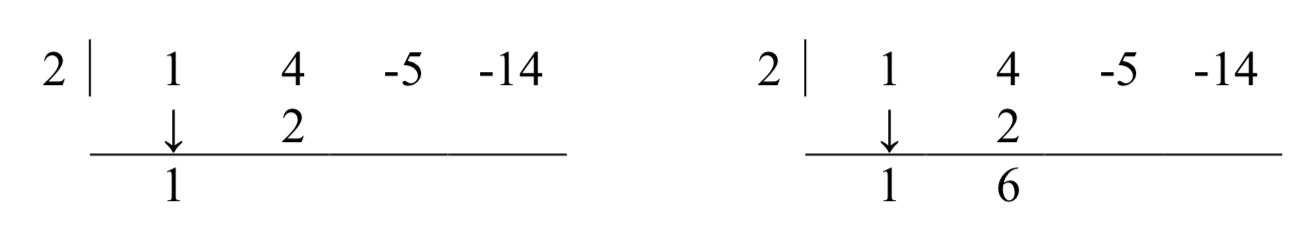
Now take the 2 from the divisor times the 6 to get 12, and add it to the -5 to get 7.

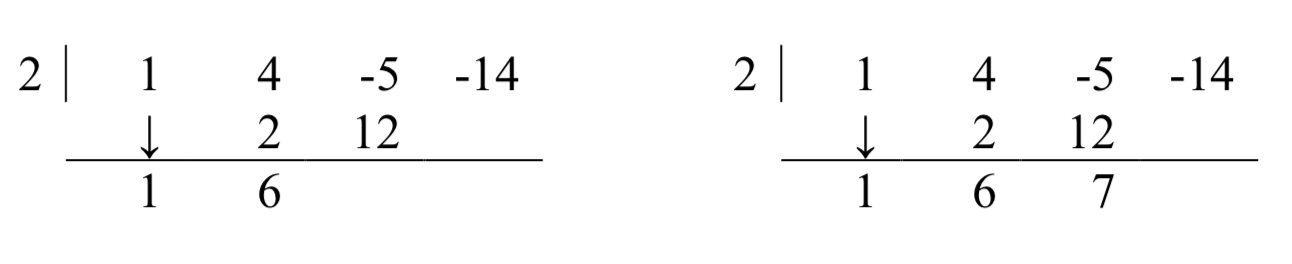
Finally, take the 2 in the divisor times the 7 to get 14, and add it to the -14 to get 0.

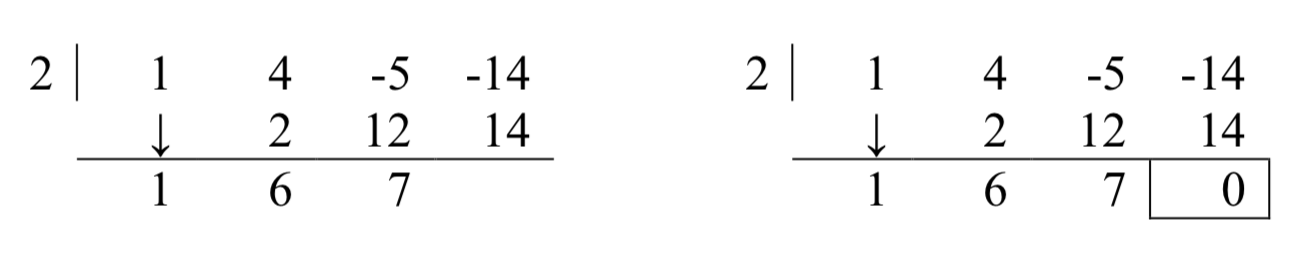
The first three numbers in the last row of our tableau are the coefficients of the quotient polynomial. Remember, we started with a third degree polynomial and divided by a first degree polynomial, so the quotient is a second degree polynomial. Hence the quotient is $x^{2} +6x+7$. The number in the box is the remainder. Synthetic division is our tool of choice for dividing polynomials by divisors of the form $x - c$. It is important to note that it works only for these kinds of divisors. Also take note that when a polynomial (of degree at least 1) is divided by $x - c$, the result will be a polynomial of exactly one less degree. Finally, it is worth the time to trace each step in synthetic division back to its corresponding step in long division.

Example $\PageIndex{3}$

Use synthetic division to divide $5x^{3} -2x^{2} +1$ by $x-3$.

Solution

When setting up the synthetic division tableau, we need to enter 0 for the coefficient of $x$ in the dividend. Doing so gives

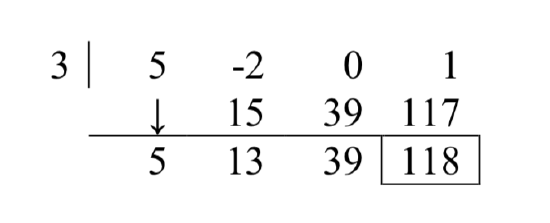
Since the dividend was a third degree polynomial, the quotient is a quadratic polynomial with coefficients 5, 13 and 39. Our quotient is $q(x)=5x^{2} +13x+39$ and the remainder is $r(x) = 118$. This means

$$5x^{3} -2x^{2} +1=(x-3)(5x^{2} +13x+39)+118\nonumber$$

It also means that $x-3$ is not a factor of $5x^{3} -2x^{2} +1$.

Example $\PageIndex{4}$

Divide $x^{3} +8$ by $x+2$.

Solution

For this division, we rewrite $x+2$ as $x-\left(-2\right)$ and proceed as before.

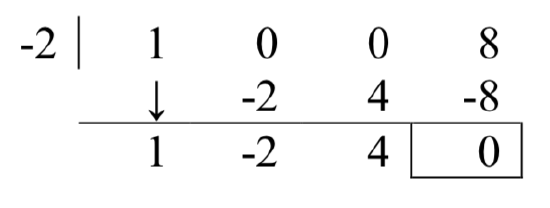
The quotient is $x^{2} -2x+4$ and the remainder is zero. Since the remainder is zero, $x+2$ is a factor of $x^{3} +8$.

$$x^{3} +8=(x+2)\left(x^{2} -2x+4\right)\nonumber$$

Exercise $\PageIndex{2}$

Divide $4x^{4} -8x^{2} -5x$ by $x-3$ using synthetic division.

Answer

$4x^4 - 8x^2 - 5x$ divided by $x -3$ is $4x^3 + 12x^2 + 28x + 79$ with remainder 237

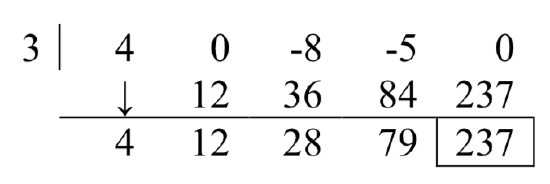
Using this process allows us to find the real zeros of polynomials, presuming we can figure out at least one root. We’ll explore how to do that in the next section.

Example $\PageIndex{5}$

The polynomial $p(x)=4x^{4} -4x^{3} -11x^{2} +12x-3$ has a horizontal intercept at $x=\dfrac{1}{2}$ with multiplicity 2. Find the other intercepts of $p(x)$.

Solution

Since $x=\dfrac{1}{2}$ is an intercept with multiplicity 2, then $x-\dfrac{1}{2}$ is a factor twice. Use synthetic division to divide by $x-\dfrac{1}{2}$ twice.

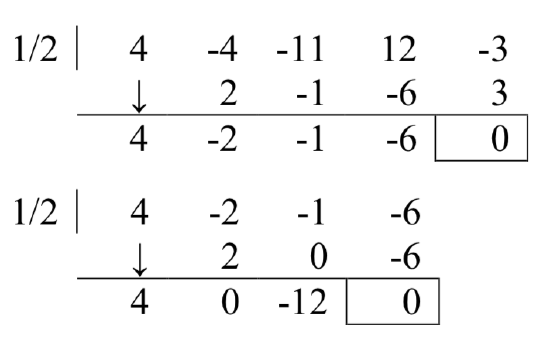
From the first division, we get $4x^{4} -4x^{3} -11x^{2} +12x-3=\left(x-\dfrac{1}{2} \right)\left(4x^{3} -2x^{2} -x-6\right)$ The second division tells us

$$4x^{4} -4x^{3} -11x^{2} +12x-3=\left(x-\dfrac{1}{2} \right)\left(x-\dfrac{1}{2} \right)\left(4x^{2} -12\right)\nonumber$$

To find the remaining intercepts, we set $4x^{2} -12=0$ and get $x=\pm \sqrt{3}$.

Note this also means $4x^{4} -4x^{3} -11x^{2} +12x-3=4\left(x-\dfrac{1}{2} \right)\left(x-\dfrac{1}{2} \right)\left(x-\sqrt{3} \right)\left(x+\sqrt{3} \right)$.

Important Topics of this Section

• Long division of polynomials
• Remainder Theorem
• Factor Theorem
• Synthetic division of polynomials