3.3E: Graphs of Polynomial Functions (Exercises)
- Page ID
- 13891
section 3.3 exercise
Find the \(C\) and \(t\) intercepts of each function.
1. \(C\left(t\right)=2\left(t-4\right)\left(t+1\right)(t-6)\)
2. \(C\left(t\right)=3\left(t+2\right)\left(t-3\right)(t+5)\)
3. \(C\left(t\right)=4t\left(t-2\right)^{2} (t+1)\)
4. \(C\left(t\right)=2t\left(t-3\right)\left(t+1\right)^{2}\)
5. \(C\left(t\right)=2t^{4} -8t^{3} +6t^{2}\)
6. \(C\left(t\right)=4t^{4} +12t^{3} -40t^{2}\)
Use your calculator or other graphing technology to solve graphically for the zeros of the function.
7. \(f\left(x\right)=x^{3} -7x^{2} +4x+30\)
8. \(g\left(x\right)=x^{3} -6x^{2} +x+28\)
Find the long run behavior of each function as \(t \to \infty\) and \(t \to -\infty\)
9. \(h\left(t\right)=3\left(t-5\right)^{3} \left(t-3\right)^{3} (t-2)\)
10. \(k\left(t\right)=2\left(t-3\right)^{2} \left(t+1\right)^{3} (t+2)\)
11. \(p\left(t\right)=-2t\left(t-1\right)\left(3-t\right)^{2}\)
12. \(q\left(t\right)=-4t\left(2-t\right)\left(t+1\right)^{3}\)
Sketch a graph of each equation.
13. \(f\left(x\right)=\left(x+3\right)^{2} (x-2)\)
14. \(g\left(x\right)=\left(x+4\right)\left(x-1\right)^{2}\)
15. \(h\left(x\right)=\left(x-1\right)^{3} \left(x+3\right)^{2}\)
16. \(k\left(x\right)=\left(x-3\right)^{3} \left(x-2\right)^{2}\)
17. \(m\left(x\right)=-2x\left(x-1\right)(x+3)\)
18. \(n\left(x\right)=-3x\left(x+2\right)(x-4)\)
Solve each inequality.
19. \(\left(x-3\right)\left(x-2\right)^{2} >0\)
20. \(\left(x-5\right)\left(x+1\right)^{2} >0\)
21. \(\left(x-1\right)\left(x+2\right)\left(x-3\right)<0\)
22. \(\left(x-4\right)\left(x+3\right)\left(x+6\right)<0\)
Find the domain of each function.
23. \(f\left(x\right)=\sqrt{-42+19x-2x^{2} }\)
24. \(g\left(x\right)=\sqrt{28-17x-3x^{2} }\)
25. \(h\left(x\right)=\sqrt{4-5x+x^{2} }\)
26. \(k\left(x\right)=\sqrt{2+7x+3x^{2} }\)
27. \(n\left(x\right)=\sqrt{\left(x-3\right)\left(x+2\right)^{2} }\)
28. \(m\left(x\right)=\sqrt{\left(x-1\right)^{2} (x+3)}\)
29. \(p\left(t\right)=\dfrac{1}{t^{2} +2t-8}\)
30. \(q\left(t\right)=\dfrac{4}{x^{2} -4x-5}\)
Write an equation for a polynomial the given features.
31. Degree 3. Zeros at \(x\) = -2, \(x\) = 1, and \(x\) = 3. Vertical intercept at (0, -4)
32. Degree 3. Zeros at \(x\) = -5, \(x\) = -2, and \(x\) = 1. Vertical intercept at (0, 6)
33. Degree 5. Roots of multiplicity 2 at \(x\) = 3 and \(x\) = 1, and a root of multiplicity 1 at \(x\) = -3. Vertical intercept at (0, 9)
34. Degree 4. Root of multiplicity 2 at \(x\) = 4, and a roots of multiplicity 1 at \(x\) = 1 and \(x\) = -2. Vertical intercept at (0, -3)
35. Degree 5. Double zero at \(x\) = 1, and triple zero at \(x\) = 3. Passes through the point (2, 15)
36. Degree 5. Single zero at \(x\) = -2 and \(x\) = 3, and triple zero at \(x\) = 1. Passes through the point (2, 4)
Write a formula for each polynomial function graphed.
37. 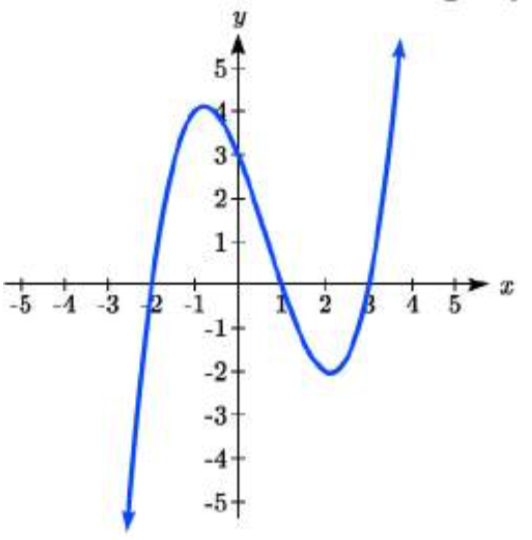 38.
38. 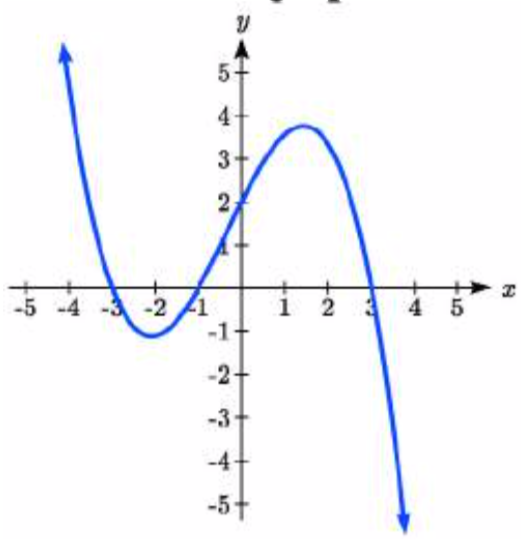 39.
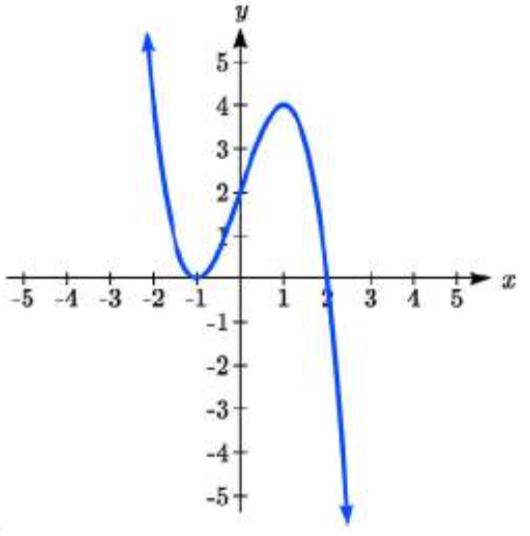
39.
40. 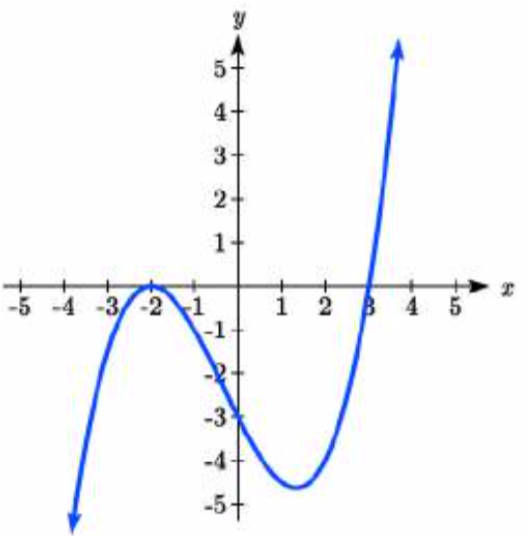 41.
41. 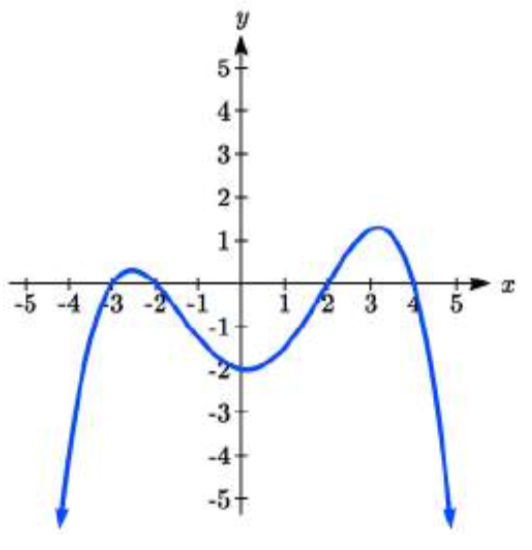 42.
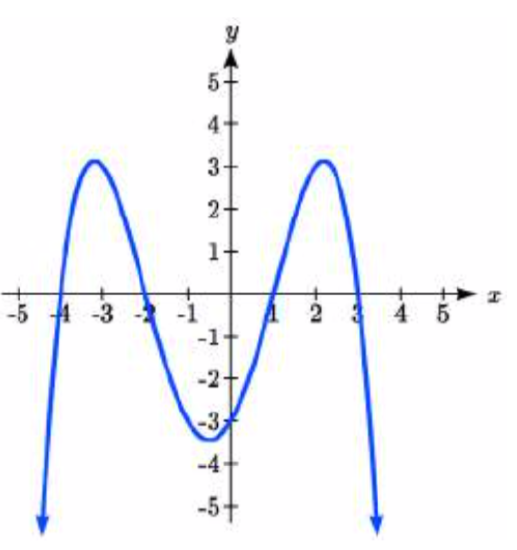
42. 
43. 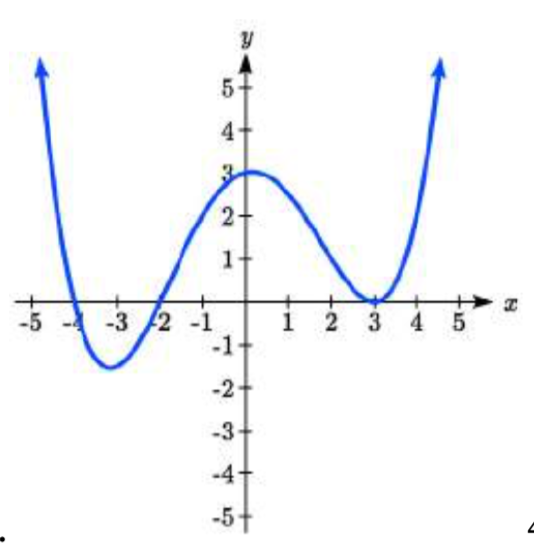 44.
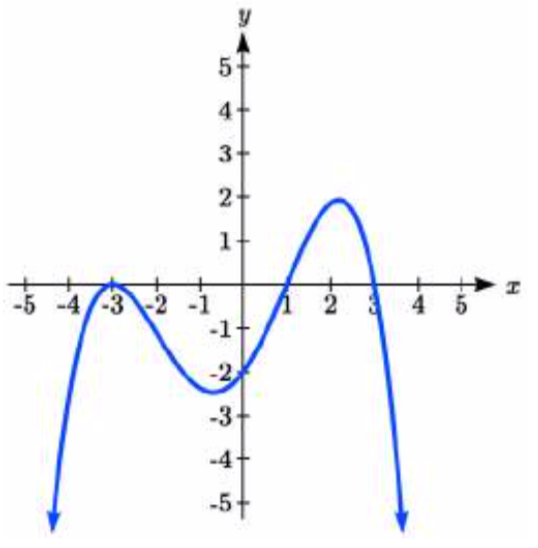
44.
Write a formula for each polynomial function graphed.
45. 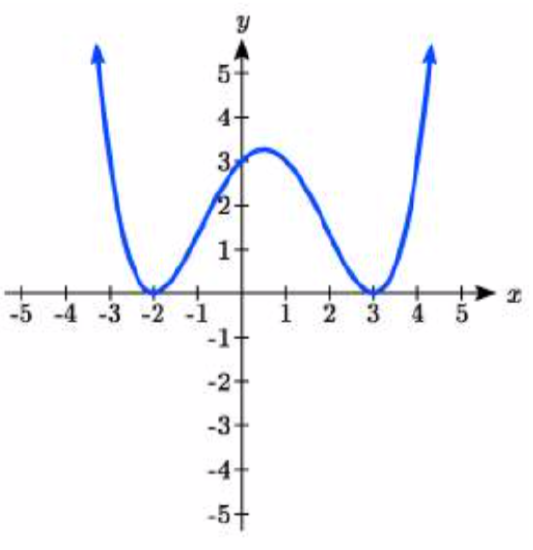 46.
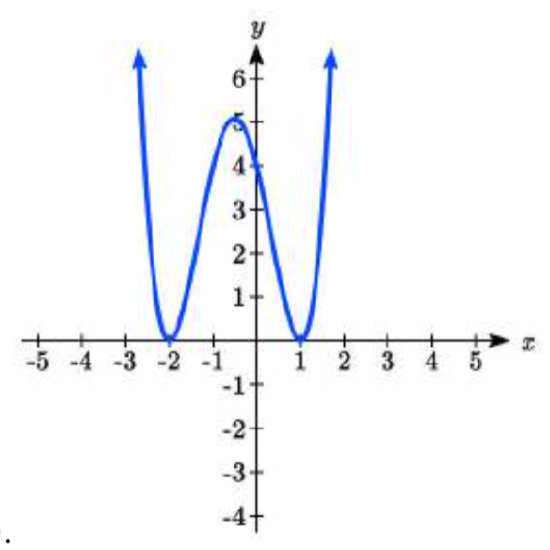
46.
47. 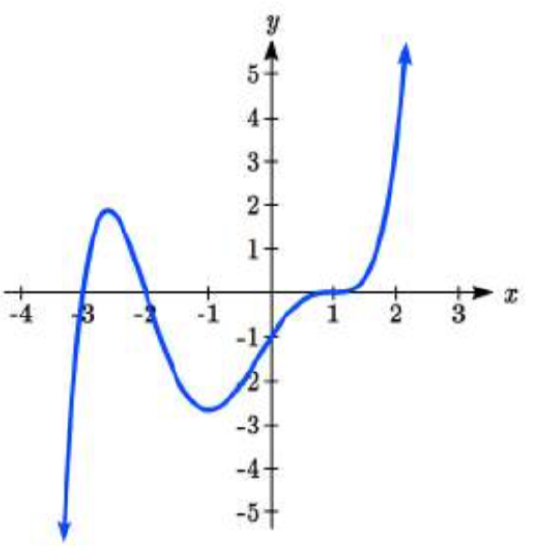 48.
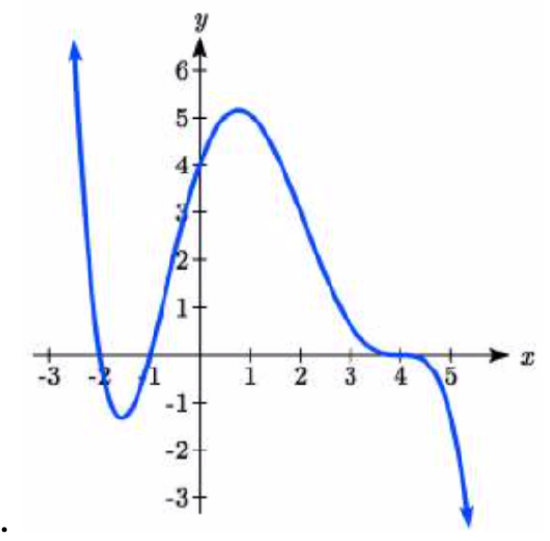
48. 
49.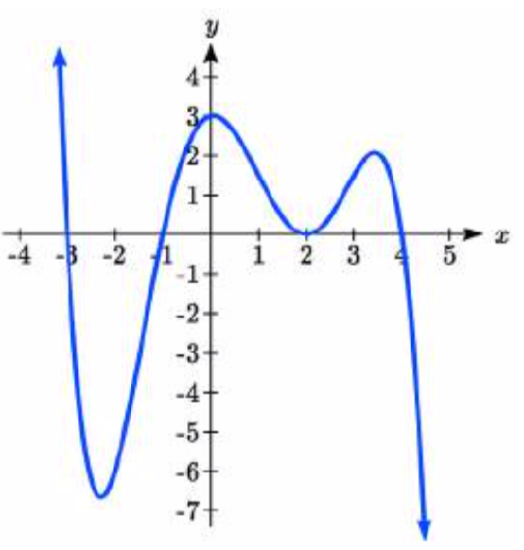 50.
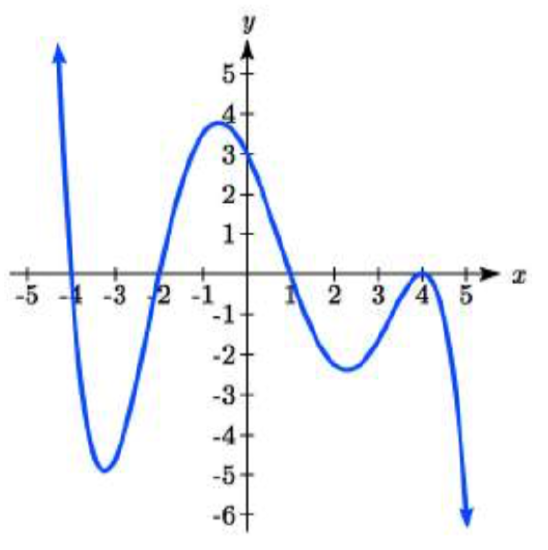
50. 
51. A rectangle is inscribed with its base on the \(x\) axis and its upper corners on the parabola \(y=5-x^{2}\). What are the dimensions of such a rectangle that has the greatest possible area?
52. A rectangle is inscribed with its base on the \(x\) axis and its upper corners on the curve \(y=16-x^{4}\). What are the dimensions of such a rectangle that has the greatest possible area?
- Answer
-
\(C(t)\) \(C\), intercepts \(t\), intercepts 1. (0, 48) (4, 0), (-1, 0), (6, 0) 3. (0, 0) (0, 0), (2, 0), (-1, 0) 5. (0, 0) (0, 0), (1, 0), (3, 0) 7. (-1.646, 0) (3.646, 0) (5, 0)
9. As \(t \to \infty\), \(h(t) \to \infty\) \(t \to -\infty\), \(h(t) \to -\infty\)
11. As \(t \to \infty\), \(p(t) \to -\infty\) \(t \to -\infty\), \(p(t) \to -\infty\)
13.
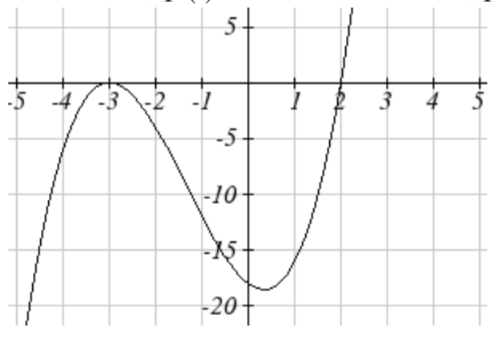
15.
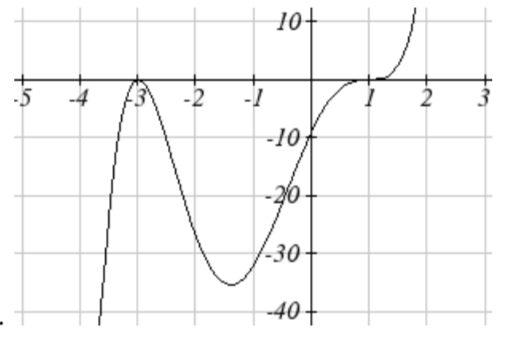
17.
19. \((3, \infty)\)
21. \((-\infty, -2) \cup (1, 3)\)
23. [3, 5, 6]
25. \((-\infty, 1] \cup [4, \infty)\)
27. \([-2, -2] \cup [3, \infty)\)
29. \((-\infty, -4) \cup (-4, 2) \cup (2, \infty)\)
31. \(y = -\dfrac{2}{3} (x + 2) (x - 1) (x - 3)\)
33. \(y = \dfrac{1}{3} (x - 1)^2 (x - 3)^2 (x + 3)\)
35. \(y = -15(x - 1)^2 (x - 3)^2\)
37. \(y = \dfrac{1}{2} (x + 2)(x - 1) (x - 3)\)
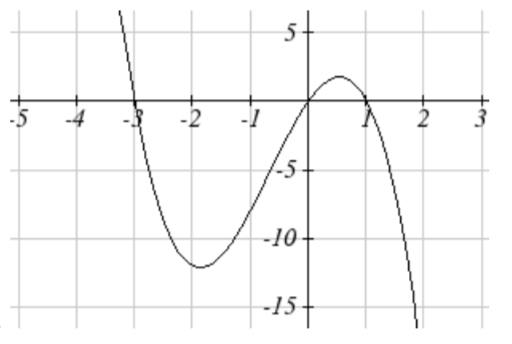
39. \(y = -(x + 1)^2 (x - 2)\)
41. \(y = -\dfrac{1}{24} (x + 3)(x + 2) (x - 2) (x - 4)\)
43. \(y = \dfrac{1}{24} (x + 4) (x + 2) (x - 3)^2\)
45. \(y = \dfrac{1}{12} (x + 2)^2 (x - 3)^2\)
47. \(y = \dfrac{1}{6} (x + 3) (x + 2) (x - 1)^3\)
49. \(y = -\dfrac{1}{16} (x + 3)(x + 1) (x - 2)^2 (x - 4)\)
51. Base 2.58, Height 3.336


