4.4: Logarithmic Properties

In the previous section, we derived two important properties of logarithms, which allowed us to solve some basic exponential and logarithmic equations.

properties of logs

Inverse Properties:

\(\log _{b} \left(b^{x} \right)=x\)

\(b^{\log _{b} x} =x\)

Exponential Property:

\(\log _{b} \left(A^{r} \right)=r\log _{b} \left(A\right)\)

Change of Base:

\(\log _{b} \left(A\right)=\frac{\log _{c} (A)}{\log _{c} (b)}\)

While these properties allow us to solve a large number of problems, they are not sufficient to solve all problems involving exponential and logarithmic equations.

properties of logs

Sum of Logs Property:

\(\log _{b} \left(A\right)+\log _{b} \left(C\right)=\log _{b} (AC)\)

Difference of Logs Property:

\(\log _{b} \left(A\right)-\log _{b} \left(C\right)=\log _{b} \left(\frac{A}{C} \right)\)

It’s just as important to know what properties logarithms do not satisfy as to memorize the valid properties listed above. In particular, the logarithm is not a linear function, which means that it does not distribute: log(\(A\) + \(B\)) \(\ne\) log(\(A\)) + log(\(B\)).

To help in this process we offer a proof to help solidify our new rules and show how they follow from properties you’ve already seen.

Let \(a=\log _{b} \left(A\right)\) and \(c=\log _{b} \left(C\right)\).

By definition of the logarithm, \(b^{a} =A\) and \(b^{c} =C\).

Using these expressions, \(AC=b^{a} b^{c}\)

Using exponent rules on the right, \(AC=b^{a+c}\)

Taking the log of both sides, and utilizing the inverse property of logs,

\(\log _{b} \left(AC\right)=\log _{b} \left(b^{a+c} \right)=a+c\)

Replacing \(a\) and \(c\) with their definition establishes the result

\(\log _{b} \left(AC\right)=\log _{b} A+\log _{b} C\)

The proof for the difference property is very similar.

With these properties, we can rewrite expressions involving multiple logs as a single log, or break an expression involving a single log into expressions involving multiple logs.

Example 1

Write \(\log _{3} \left(5\right)+\log _{3} \left(8\right)-\log _{3} \left(2\right)\) as a single logarithm.

Solution

Using the sum of logs property on the first two terms,

\(\log _{3} \left(5\right)+\log _{3} \left(8\right)=\log _{3} \left(5\cdot 8\right)=\log _{3} \left(40\right)\)

This reduces our original expression to \(\log _{3} \left(40\right)-\log _{3} \left(2\right)\)

Then using the difference of logs property,

\(\log _{3} \left(40\right)-\log _{3} \left(2\right)=\log _{3} \left(\frac{40}{2} \right)=\log _{3} \left(20\right)\)

Example 2

Evaluate \(2\log \left(5\right)+\log \left(4\right)\) without a calculator by first rewriting as a single logarithm.

Solution

On the first term, we can use the exponent property of logs to write

\(2\log \left(5\right)=\log \left(5^{2} \right)=\log \left(25\right)\)

With the expression reduced to a sum of two logs, \(\log \left(25\right)+\log \left(4\right)\), we can utilize the sum of logs property

\(\log \left(25\right)+\log \left(4\right)=\log (4\cdot 25)=\log (100)\)

Since 100 = 10\({}^{2}\), we can evaluate this log without a calculator:

\(\log (100)=\log \left(10^{2} \right)=2\)

Exercise

Without a calculator evaluate by first rewriting as a single logarithm:

\(\log _{2} \left(8\right)+\log _{2} \left(4\right)\)

Answer

\(\log _{2} \left(8\cdot 4\right)=\log _{2} \left(32\right)=\log _{2} \left(2^{5} \right)=5\)

Example 3

Rewrite \(\ln \left(\frac{x^{4} y}{7} \right)\) as a sum or difference of logs

Solution

First, noticing we have a quotient of two expressions, we can utilize the difference property of logs to write

\(\ln \left(\frac{x^{4} y}{7} \right)=\ln \left(x^{4} y\right)-\ln (7)\)

Then seeing the product in the first term, we use the sum property

\(\ln \left(x^{4} y\right)-\ln (7)=\ln \left(x^{4} \right)+\ln (y)-\ln (7)\)

Finally, we could use the exponent property on the first term

\(\ln \left(x^{4} \right)+\ln (y)-\ln (7)=4\ln (x)+\ln (y)-\ln (7)\)

I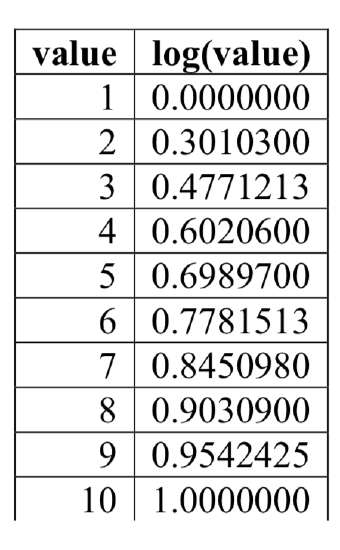nterestingly, solving exponential equations was not the reason logarithms were originally developed. Historically, up until the advent of calculators and computers, the power of logarithms was that these log properties reduced multiplication, division, roots, or powers to be evaluated using addition, subtraction, division and multiplication, respectively, which are much easier to compute without a calculator. Large books were published listing the logarithms of numbers, such as in the table to the right. To find the product of two numbers, the sum of log property was used. Suppose for example we didn’t know the value of 2 times 3. Using the sum property of logs:

\(\log (2\cdot 3)=\log (2)+\log (3)\)

Using the log table, \[\log (2\cdot 3)=\log (2)+\log (3)=0.3010300+0.4771213=0.7781513\]

We can then use the table again in reverse, looking for 0.7781513 as an output of the logarithm. From that we can determine:

\(\log (2\cdot 3)=0.7781513=\log (6).\)

By using addition and the table of logs, we were able to determine\(2\cdot 3=6\).

Likewise, to compute a cube root like \(\sqrt[{3}]{8}\)

\(\log (\sqrt[{3}]{8} )==\log \left(8^{1/3} \right)=\frac{1}{3} \log (8)=\frac{1}{3} (0.9030900)=0.3010300=\log (2)\)

So \(\sqrt[{3}]{8} =2\).

Although these calculations are simple and insignificant, they illustrate the same idea that was used for hundreds of years as an efficient way to calculate the product, quotient, roots, and powers of large and complicated numbers, either using tables of logarithms or mechanical tools called slide rules.

These properties still have other practical applications for interpreting changes in exponential and logarithmic relationships.

Example 4

Recall that in chemistry,\(pH=-\log \left(\left[H^{+} \right]\right)\). If the concentration of hydrogen ions in a liquid is doubled, what is the affect on pH?

Solution

Suppose \(C\) is the original concentration of hydrogen ions, and \(P\) is the original pH of the liquid, so \(P=-\log \left(C\right)\). If the concentration is doubled, the new concentration is \(2C\). Then the pH of the new liquid is

\(pH=-\log \left(2C\right)\)

Using the sum property of logs,

\(pH=-\log \left(2C\right)=-\left(\log (2)+\log (C)\right)=-\log (2)-\log (C)\)

Since \(P=-\log \left(C\right)\), the new pH is

\(pH=P-\log (2)=P-0.301\)

When the concentration of hydrogen ions is doubled, the pH decreases by 0.301.

Log properties in solving equations

The logarithm properties often arise when solving problems involving logarithms. First, we’ll look at a simpler log equation.

Example 5

Solve \(\log (2x-6)=3\).

Solution

To solve for \(x\), we need to get it out from inside the log function. There are two ways we can approach this.

Method 1: Rewrite as an exponential.

Recall that since the common log is base 10, \(\log (A)=B\) can be rewritten as the exponential \(10^{B} =A\). Likewise, \(\log (2x-6)=3\) can be rewritten in exponential form as

\(10^{3} =2x-6\)

Method 2: Exponentiate both sides.

If \(A=B\), then \(10^{A} =10^{B}\). Using this idea, since \(\log (2x-6)=3\), then \(10^{\log (2x-6)} =10^{3}\). Use the inverse property of logs to rewrite the left side and get \(2x-6=10^{3}\).

Using either method, we now need to solve \(2x-6=10^{3}\). Evaluate \(10^{3}\) to get

\(2x-6=1000\) Add 6 to both sides
\(2x=1006\) Divide both sides by 2
\(x=503\)

Occasionally the solving process will result in extraneous solutions – answers that are outside the domain of the original equation. In this case, our answer looks fine.

Example 6

Solve \(\log (50x+25)-\log (x)=2\).

Solution

In order to rewrite in exponential form, we need a single logarithmic expression on the left side of the equation. Using the difference property of logs, we can rewrite the left side:

\(\log \left(\frac{50x+25}{x} \right)=2\)

Rewriting in exponential form reduces this to an algebraic equation:

\(\frac{50x+25}{x} =10^{2} =100\) Multiply both sides by \(x\)
\(50x+25=100x\) Combine like terms
\(25=50x\) Divide by 50
\(x=\frac{25}{50} =\frac{1}{2}\)

Checking this answer in the original equation, we can verify there are no domain issues, and this answer is correct.

Exercise

Solve \(\log (x^{2} -4)=1+\log (x+2)\).

Answer

\(\log (x^{2} -4)=1+\log (x+2)\) Move both logs to one side

\(\log \left(x^{2} -4\right)-\log \left(x+2\right)=1\) Use the difference property of logs

\(\log \left(\frac{x^{2} -4}{x+2} \right)=1\) Factor

\(\log \left(\frac{(x+2)(x-2)}{x+2} \right)=1\) Simplify

\(\log \left(x-2\right)=1\) Rewrite as an exponential

\(10^{1} =x-2\) Add 2 to both sides

\(x=12\)

Example 7

Solve \(\ln (x+2)+\ln (x+1)=\ln (4x+14)\).

Solution

\(\ln (x+2)+\ln (x+1)=\ln (4x+14)\) Use the sum of logs property on the right
\(\ln \left((x+2)(x+1)\right)=\ln (4x+14)\) Expand
\(\ln \left(x^{2} +3x+2\right)=\ln (4x+14)\)

We have a log on both side of the equation this time. Rewriting in exponential form would be tricky, so instead we can exponentiate both sides.

\(e^{\ln \left(x^{2} +3x+2\right)} =e^{\ln (4x+13)}\) Use the inverse property of logs
\(x^{2} +3x+2=4x+14\) Move terms to one side
\(x^{2} -x-12=0\) Factor
\((x+4)(x-3)=0\)
\(x = -4\) or \(x = 3\).

Checking our answers, notice that evaluating the original equation at \(x = -4\) would result in us evaluating \(\ln (-2)\), which is undefined. That answer is outside the domain of the original equation, so it is an extraneous solution and we discard it. There is one solution: \(x = 3\).

More complex exponential equations can often be solved in more than one way. In the following example, we will solve the same problem in two ways – one using logarithm properties, and the other using exponential properties.

Example 8a

In 2008, the population of Kenya was approximately 38.8 million, and was growing by 2.64% each year, while the population of Sudan was approximately 41.3 million and growing by 2.24% each year(World Bank, World Development Indicators, as reported on http://www.google.com/publicdata, retrieved August 24, 2010). If these trends continue, when will the population of Kenya match that of Sudan?

Solution

We start by writing an equation for each population in terms of \(t\), the number of years after 2008.

\(\begin{array}{l} {Kenya(t)=38.8(1+0.0264)^{t} } \\ {Sudan(t)=41.3(1+0.0224)^{t} } \end{array}\)

To find when the populations will be equal, we can set the equations equal

\(38.8(1.0264)^{t} =41.3(1.0224)^{t}\)

For our first approach, we take the log of both sides of the equation.

\(\log \left(38.8(1.0264)^{t} \right)=\log \left(41.3(1.0224)^{t} \right)\)

Utilizing the sum property of logs, we can rewrite each side,

\(\log (38.8)+\log \left(1.0264^{t} \right)=\log (41.3)+\log \left(1.0224^{t} \right)\)

Then utilizing the exponent property, we can pull the variables out of the exponent

\(\log (38.8)+t\log \left(1.0264\right)=\log (41.3)+t\log \left(1.0224\right)\)

Moving all the terms involving \(t\) to one side of the equation and the rest of the terms to the other side,

\(t\log \left(1.0264\right)-t\log \left(1.0224\right)=\log (41.3)-\log (38.8)\)

Factoring out the \(t\) on the left,

\(t\left(\log \left(1.0264\right)-\log \left(1.0224\right)\right)=\log (41.3)-\log (38.8)\)

Dividing to solve for \(t\)

\(t=\frac{\log (41.3)-\log (38.8)}{\log \left(1.0264\right)-\log \left(1.0224\right)} \approx 15.991\) years until the populations will be equal.

Example 8b

Solve the problem above by rewriting before taking the log.

Solution

Starting at the equation

\(38.8(1.0264)^{t} =41.3(1.0224)^{t}\)

Divide to move the exponential terms to one side of the equation and the constants to the other side

\(\frac{1.0264^{t} }{1.0224^{t} } =\frac{41.3}{38.8}\)

Using exponent rules to group on the left,

\(\left(\frac{1.0264}{1.0224} \right)^{t} =\frac{41.3}{38.8}\)

Taking the log of both sides

\(\log \left(\left(\frac{1.0264}{1.0224} \right)^{t} \right)=\log \left(\frac{41.3}{38.8} \right)\)

Utilizing the exponent property on the left,

\(t\log \left(\frac{1.0264}{1.0224} \right)=\log \left(\frac{41.3}{38.8} \right)\)

Dividing gives

\(t=\frac{\log \left(\frac{41.3}{38.8} \right)}{\log \left(\frac{1.0264}{1.0224} \right)} \approx 15.991\) years

While the answer does not immediately appear identical to that produced using the previous method, note that by using the difference property of logs, the answer could be rewritten:

\(t=\frac{\log \left(\frac{41.3}{38.8} \right)}{\log \left(\frac{1.0264}{1.0224} \right)} =\frac{\log (41.3)-\log (38.8)}{\log (1.0264)-\log (1.0224)}\)

While both methods work equally well, it often requires fewer steps to utilize algebra before taking logs, rather than relying solely on log properties.

Exercise

Tank A contains 10 liters of water, and 35% of the water evaporates each week. Tank B contains 30 liters of water, and 50% of the water evaporates each week. In how many weeks will the tanks contain the same amount of water?

Answer

Tank A: \(A(t)=10(1-0.35)^{t}\). Tank B: \(B(t)=30(1-0.50)^{t}\)

Solving A(t) = B(t),

\(10(0.65)^{t} =30(0.5)^{t}\) Using the method from Example 8b

\(\frac(0.65)^{t} }(0.5)^{t} } =\frac{30}{10}\) Regroup

\(\left(\frac{0.65}{0.5} \right)^{t} =3\) Simplify

\(\left(1.3\right)^{t} =3\) Take the log of both sides

\(\log \left(\left(1.3\right)^{t} \right)=\log \left(3\right)\) Use the exponent property of logs

\(t\log \left(1.3\right)=\log \left(3\right)\) Divide and evaluate

\(t=\frac{\log \left(3\right)}{\log \left(1.3\right)} \approx 4.1874\) weeks

Important Topics of this Section

• Inverse
• Exponential
• Change of base
• Sum of logs property
• Difference of logs property