4.6E: Exponential and Logarithmic Models (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Section 4.6 Exercise
1. You go to the doctor and he injects you with 13 milligrams of radioactive dye. After 12 minutes, 4.75 milligrams of dye remain in your system. To leave the doctor’s office, you must pass through a radiation detector without sounding the alarm. If the detector will sound the alarm whenever more than 2 milligrams of the dye are in your system, how long will your visit to the doctor take, assuming you were given the dye as soon as you arrived and the amount of dye decays exponentially?
2. You take 200 milligrams of a headache medicine, and after 4 hours, 120 milligrams remain in your system. If the effects of the medicine wear off when less than 80 milligrams remain, when will you need to take a second dose, assuming the amount of medicine in your system decays exponentially?
3. The half-life of Radium-226 is 1590 years. If a sample initially contains 200 mg, how many milligrams will remain after 1000 years?
4. The half-life of Fermium-253 is 3 days. If a sample initially contains 100 mg, how many milligrams will remain after 1 week?
5. The half-life of Erbium-165 is 10.4 hours. After 24 hours a sample still contains 2 mg. What was the initial mass of the sample, and how much will remain after another 3 days?
6. The half-life of Nobelium-259 is 58 minutes. After 3 hours a sample still contains10 mg. What was the initial mass of the sample, and how much will remain after another 8 hours?
7. A scientist begins with 250 grams of a radioactive substance. After 225 minutes, the sample has decayed to 32 grams. Find the half-life of this substance.
8. A scientist begins with 20 grams of a radioactive substance. After 7 days, the sample has decayed to 17 grams. Find the half-life of this substance.
9. A wooden artifact from an archeological dig contains 60 percent of the carbon-14 that is present in living trees. How long ago was the artifact made? (The half-life of carbon-14 is 5730 years.)
10. A wooden artifact from an archeological dig contains 15 percent of the carbon-14 that is present in living trees. How long ago was the artifact made? (The half-life of carbon-14 is 5730 years.)
11. A bacteria culture initially contains 1500 bacteria and doubles in size every half hour. Find the size of the population after: a) 2 hours b) 100 minutes
12. A bacteria culture initially contains 2000 bacteria and doubles in size every half hour. Find the size of the population after: a) 3 hours b) 80 minutes
13. The count of bacteria in a culture was 800 after 10 minutes and 1800 after 40 minutes.
a. What was the initial size of the culture?
b. Find the doubling time.
c. Find the population after 105 minutes.
d. When will the population reach 11000?
14. The count of bacteria in a culture was 600 after 20 minutes and 2000 after 35 minutes.
a. What was the initial size of the culture?
b. Find the doubling time.
c. Find the population after 170 minutes.
d. When will the population reach 12000?
15. Find the time required for an investment to double in value if invested in an account paying 3% compounded quarterly.
16. Find the time required for an investment to double in value if invested in an account paying 4% compounded monthly
17. The number of crystals that have formed after t hours is given by n(t)=20e0.013t. How long does it take the number of crystals to double?
18. The number of building permits in Pasco t years after 1992 roughly followed the equation n(t)=400e0.143t. What is the doubling time?
19. A turkey is pulled from the oven when the internal temperature is 165∘ Fahrenheit, and is allowed to cool in a 75∘ room. If the temperature of the turkey is 145∘ after half an hour,
a. What will the temperature be after 50 minutes?
b. How long will it take the turkey to cool to 110∘?
20. A cup of coffee is poured at 190∘ Fahrenheit, and is allowed to cool in a 70∘ room. If the temperature of the coffee is 170∘ after half an hour,
a. What will the temperature be after 70 minutes?
b. How long will it take the coffee to cool to 120∘\)?
21. The population of fish in a farm-stocked lake after t years could be modeled by the equation P(t)=10001+9e−0.6t.
a. Sketch a graph of this equation.
b. What is the initial population of fish?
c. What will the population be after 2 years?
d. How long will it take for the population to reach 900?
22. The number of people in a town who have heard a rumor after t days can be modeled by the equation N(t)=5001+49e−0.7t.
a. Sketch a graph of this equation.
b. How many people started the rumor?
c. How many people have heard the rumor after 3 days?
d. How long will it take until 300 people have heard the rumor?
Find the value of the number shown on each logarithmic scale
23.  24.
24.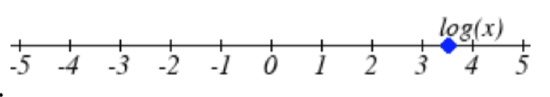
25. 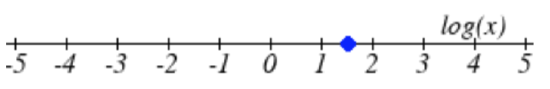 26.
26.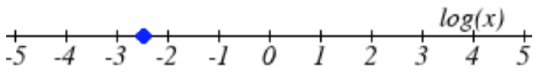
Plot each set of approximate values on a logarithmic scale.
27. Intensity of sounds: Whisper: 10−10W/m2, Vacuum: 10−4W/m2, Jet: 102W/m2
28. Mass: Amoeba: 10−5g, Human: 105g, Statue of Liberty: 108g
29. The 1906 San Francisco earthquake had a magnitude of 7.9 on the MMS scale. Later there was an earthquake with magnitude 4.7 that caused only minor damage. How many times more intense was the San Francisco earthquake than the second one?
30. The 1906 San Francisco earthquake had a magnitude of 7.9 on the MMS scale. Later there was an earthquake with magnitude 6.5 that caused less damage. How many times more intense was the San Francisco earthquake than the second one?
31. One earthquake has magnitude 3.9 on the MMS scale. If a second earthquake has 750 times as much energy as the first, find the magnitude of the second quake.
32. One earthquake has magnitude 4.8 on the MMS scale. If a second earthquake has 1200 times as much energy as the first, find the magnitude of the second quake.
33. A colony of yeast cells is estimated to contain 106 cells at time t=0. After collecting experimental data in the lab, you decide that the total population of cells at time t hours is given by the function f(t)=106e0.495105t. [UW]
a. How many cells are present after one hour?
b. How long does it take of the population to double?.
c. Cherie, another member of your lab, looks at your notebook and says: “That formula is wrong, my calculations predict the formula for the number of yeast cells is given by the function. f(t)=106(2.042727)0.693147t.” Should you be worried by Cherie’s remark?
d. Anja, a third member of your lab working with the same yeast cells, took these two measurements: 7.246×106 cells after 4 hours; 16.504×106 cells after 6 hours. Should you be worried by Anja’s results? If Anja’s measurements are correct, does your model over estimate or under estimate the number of yeast cells at time t?
34. As light from the surface penetrates water, its intensity is diminished. In the clear waters of the Caribbean, the intensity is decreased by 15 percent for every 3 meters of depth. Thus, the intensity will have the form of a general exponential function. [UW]
a. If the intensity of light at the water’s surface isI0, find a formula for I(d), the intensity of light at a depth of d meters. Your formula should depend on I0and d.
b. At what depth will the light intensity be decreased to 1% of its surface intensity?
35. Myoglobin and hemoglobin are oxygen-carrying molecules in the human body. Hemoglobin is found inside red blood cells, which flow from the lungs to the muscles through the bloodstream. Myoglobin is found in muscle cells. The function Y=M(p)=p1+p calculates the fraction of myoglobin saturated with oxygen at a given pressure p Torrs. For example, at a pressure of 1 Torr, M(1)=0.5, which means half of the myoglobin (i.e. 50%) is oxygen saturated. (Note: More precisely, you need to use something called the “partial pressure”, but the distinction is not important for this problem.) Likewise, the function Y=H(p)=p2.8262.8+p2.8 calculates the fraction of hemoglobin saturated with oxygen at a given pressure p. [UW]
a. The graphs of M(p) and H(p) are given here on the domain 0≤p≤100; which is which?
b. If the pressure in the lungs is 100 Torrs, what is the level of oxygen saturation of the hemoglobin in the lungs?
c. The pressure in an active muscle is 20 Torrs. What is the level of oxygen saturation of myoglobin in an active muscle? What is the level of hemoglobin in an active muscle?
d. Define the efficiency of oxygen transport at a given pressure p to be M(p)−H(p). What is the oxygen transport efficiency at 20 Torrs? At 40 Torrs? At 60 Torrs? Sketch the graph of M(p)−H(p); are there conditions under which transport efficiency is maximized (explain)?
36. The length of some fish are modeled by a von Bertalanffy growth function. For Pacific halibut, this function has the form L(t)=200(1−0.957e−0.18t) where L(t) is the length (in centimeters) of a fish t years old. [UW]
a. What is the length of a newborn halibut at birth?
b. Use the formula to estimate the length of a 6–year–old halibut.
c. At what age would you expect the halibut to be 120 cm long?
d. What is the practical (physical) significance of the number 200 in the formula for L(t)?
37. A cancer cell lacks normal biological growth regulation and can divide continuously. Suppose a single mouse skin cell is cancerous and its mitotic cell cycle (the time for the cell to divide once) is 20 hours. The number of cells at time t grows according to an exponential model. [UW]
a. Find a formula C(t) for the number of cancerous skin cells after t hours.
b. Assume a typical mouse skin cell is spherical of radius 50×10−4 cm. Find the combined volume of all cancerous skin cells after t hours. When will the volume of cancerous cells be 1 cm3?
38. A ship embarked on a long voyage. At the start of the voyage, there were 500 ants in the cargo hold of the ship. One week into the voyage, there were 800 ants. Suppose the population of ants is an exponential function of time. [UW]
a. How long did it take the population to double?
b. How long did it take the population to triple?
c. When were there be 10,000 ants on board?
d. There also was an exponentially growing population of anteaters on board. At the start of the voyage there were 17 anteaters, and the population of anteaters doubled every 2.8 weeks. How long into the voyage were there 200 ants per anteater?
39. The populations of termites and spiders in a certain house are growing exponentially. The house contains 100 termites the day you move in. After 4 days, the house contains 200 termites. Three days after moving in, there are two times as many termites as spiders. Eight days after moving in, there were four times as many termites as spiders. How long (in days) does it take the population of spiders to triple? [UW]
- Answer
-
1. f(t)=13(0.9195)t. 2 mg will remain after 22.3098 minutes
3. f(t)=200(0.999564)t. f(1000)=129.3311 mg
5. r=−0.06448. Initial mass: 9.9018 mg. After 3 days: 0.01648 mg
7. f(t)=250(0.9909)t. Half-life = 75.8653 minutes
9. f(t)=a(0.999879)t. 60% (0.60a) would remain after 4222.813 years
11. P(t)=1500(1.02337)t (t in minutes).
After 2 hours = 24000.
After 100 minutes = 1511913. a) 610.5143 (about 611)
b) 25. 6427 minutes
c) 10431.21
d). 106.9642 minutes15. 23.1914 years
17. 53.319 hours
19. T(t)=.90(0.99166)t+75.
a). 134.212 deg
b). 112.743 minutes21. a).
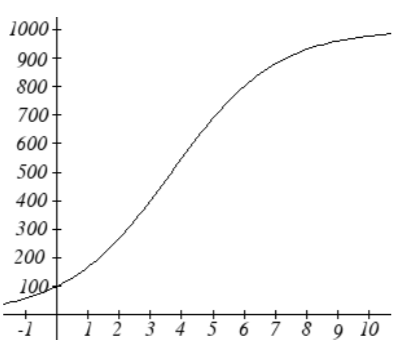
b). 100
c). 269.487
d). 7.324 years23. log(x)=−0.5.x=0.3162
25. log(x).=1.5.x=31.623
27.

29. 63095.7 times more intense
31. MMS magnitude 5.817
33. a). about 1640671
b). 1.4 hours
c). No, because (2.042727)0.693147≈e0.495104
d). Anja’s data predicts a continuous growth rate of 0.4116, which is much smaller than the rate 0.495105 you calculated. Our model would overestimate the number of cells.35. a) The curve that increases rapidly at first is M(p)
b) H(100)=0.9775
c) Myoglobin: M(20)=0.9524. Hemoglobin: H(20)=0.3242
d) At 20 torrs: 0.6282. At 40 torrs: 0.2060. At 60 torrs: 0.0714
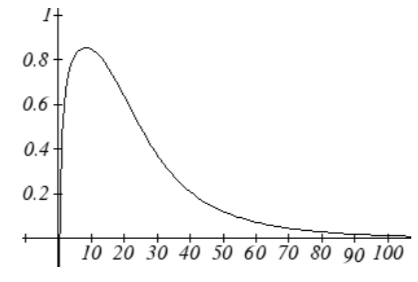 Efficiency seems to be maximized at about 8 torr
Efficiency seems to be maximized at about 8 torr37. a) C(t)=1.03526t, or C(t)=e0.03466t
b) Volume of one cell: 43π(50×10−4)3≈5.236×10−7cm3, so will need about 1.9099×106 cells for a volume of 1 cm3. C(t)=1.9099×106 after 417.3 hours39. 31.699 days


