4.7: Fitting Exponential Models to Data
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the previous section, we saw number lines using logarithmic scales. It is also common to see two dimensional graphs with one or both axes using a logarithmic scale.
One common use of a logarithmic scale on the vertical axis is to graph quantities that are changing exponentially, since it helps reveal relative differences. This is commonly used in stock charts, since values historically have grown exponentially over time. Both stock charts below show the Dow Jones Industrial Average, from 1928 to 2010.
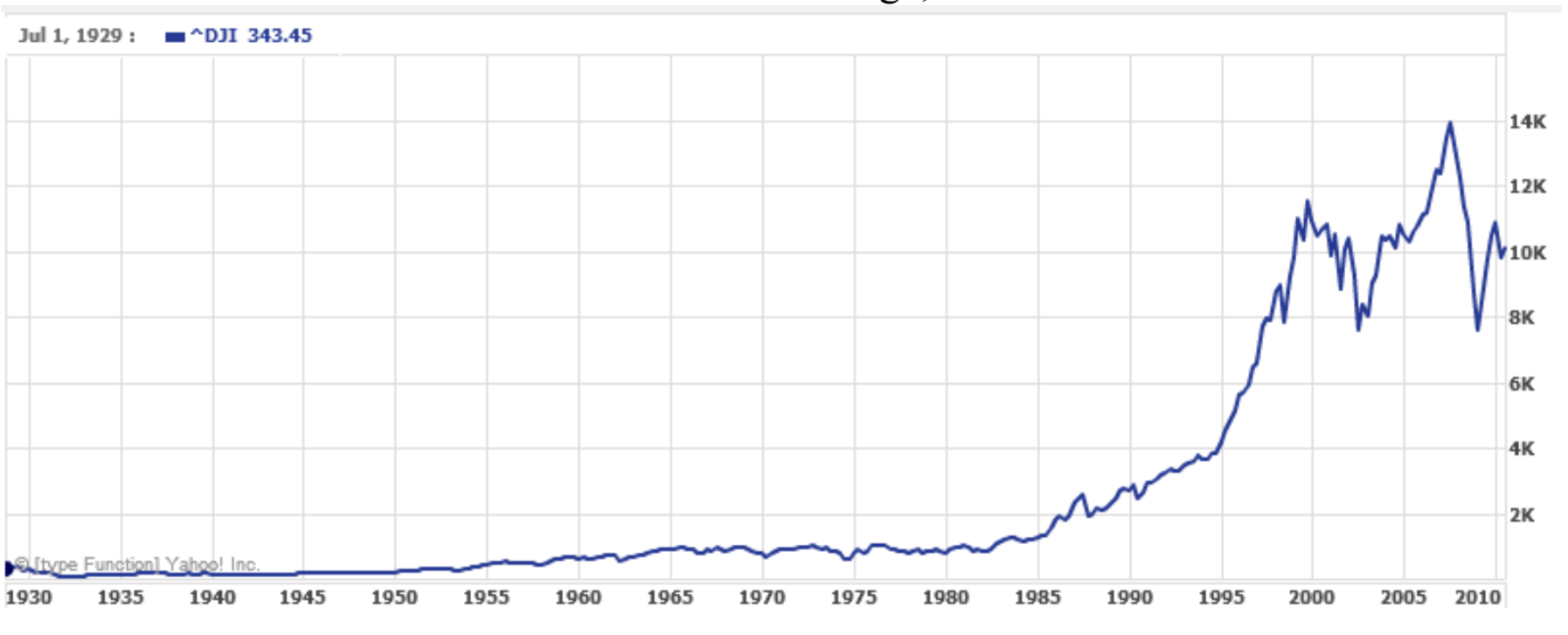
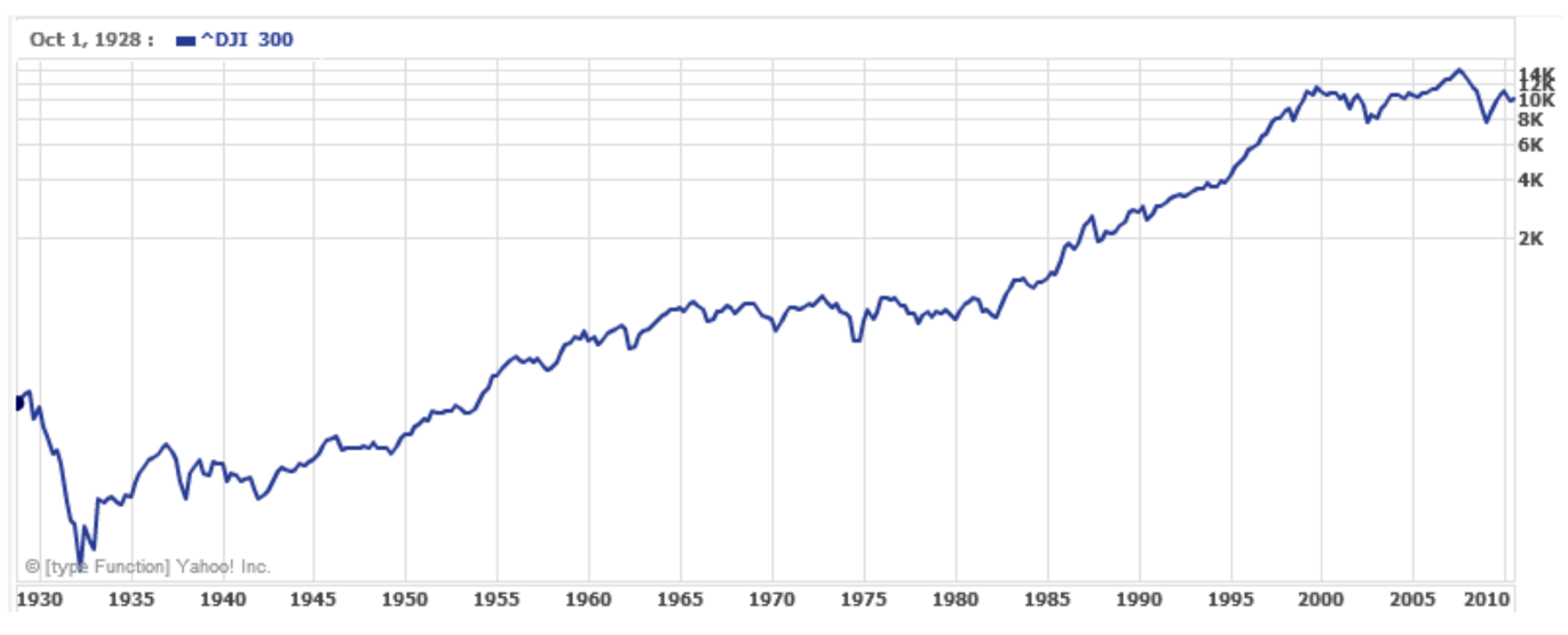
Both charts have a linear horizontal scale, but the first graph has a linear vertical scale, while the second has a logarithmic vertical scale. The first scale is the one we are more familiar with, and shows what appears to be a strong exponential trend, at least up until the year 2000.
Example 4.7.1
There were stock market drops in 1929 and 2008. Which was larger?
Solution
In the first graph, the stock market drop around 2008 looks very large, and in terms of dollar values, it was indeed a large drop. However, the second graph shows relative changes, and the drop in 2009 seems less major on this graph, and in fact the drop starting in 1929 was, percentage-wise, much more significant.
Specifically, in 2008, the Dow value dropped from about 14,000 to 8,000, a drop of 6,000. This is obviously a large value drop, and amounts to about a 43% drop. In 1929, the Dow value dropped from a high of around 380 to a low of 42 by July of 1932. While value-wise this drop of 338 is much smaller than the 2008 drop, it corresponds to a 89% drop, a much larger relative drop than in 2008. The logarithmic scale shows these relative changes.
The second graph above, in which one axis uses a linear scale and the other axis uses a logarithmic scale, is an example of a semi-log graph.
Definition: Semi-log and log-log GRAPHS
A semi-log graph is a graph with one axis using a linear scale and one axis using a logarithmic scale.
A log-log graph is a graph with both axes using logarithmic scales.
Example 4.7.2
Plot 5 points on the graph off(x)=3(2)x on a semi-log graph with a logarithmic scale on the vertical axis.
Solution
To do this, we need to find 5 points on the graph, then calculate the logarithm of the output value. Arbitrarily choosing 5 input values,
| x | f(x) | log(f(x)) |
| -3 | 3(2)−1=38 | -0.426 |
| -1 | 3(2)−1=32 | 0.176 |
| 0 | 3(2)0=3 | 0.477 |
| 2 | 3(2)2=12 | 1.079 |
| 5 | 3(2)5=96 | 1.982 |
Plotting these values on a semi-log graph,
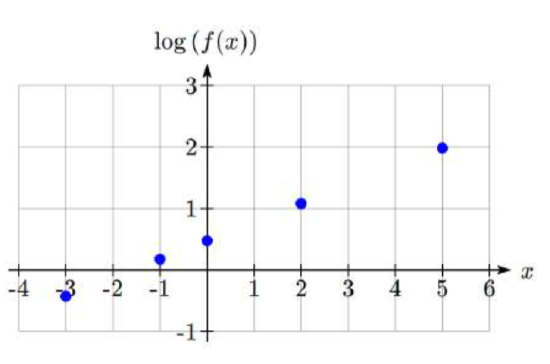
Notice that on this semi-log scale, values from the exponential function appear linear. We can show this behavior is expected by utilizing logarithmic properties. For the function f(x)=abx, finding log(f(x)) gives
log(f(x))=log(abx) Utilizing the sum property of logs,
log(f(x))=log(a)+log(bx) Now utilizing the exponent property,
log(f(x))=log(a)+xlog(b)
This relationship is linear, with log(a) as the vertical intercept, and log(b) as the slope. This relationship can also be utilized in reverse.
Example 4.7.3
An exponential graph is plotted on semi-log axes. Find a formula for the exponential function g(x) that generated this graph.
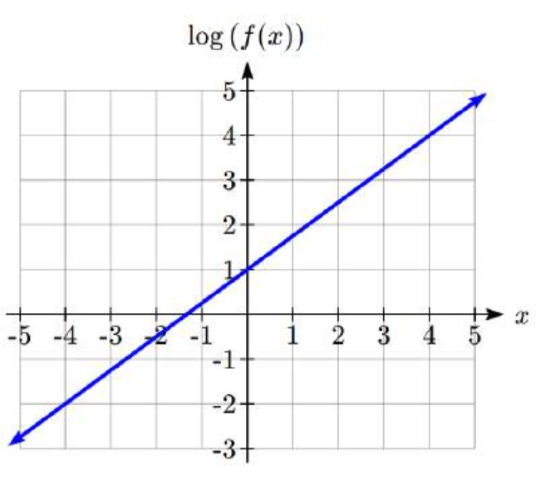
Solution
The graph is linear, with vertical intercept at (0, 1). Looking at the change between the points (0, 1) and (4, 4), we can determine the slope of the line is 34. Since the output is log(g(x)), this leads to the equation log(g(x))=1+34x.
We can solve this formula for g(x) by rewriting in exponential form and simplifying:
log(g(x))=1+34x Rewriting as an exponential,
g(x)=101+34x Breaking this apart using exponent rules,
g(x)=101⋅1034x Using exponent rules to group the second factor,
g(x)=101⋅(1034)x Evaluating the powers of 10,
g(x)=10(5.623)x
Exercise 4.7.1
An exponential graph is plotted on a semi-log graph below. Find a formula for the exponential function g(x) that generated this graph.
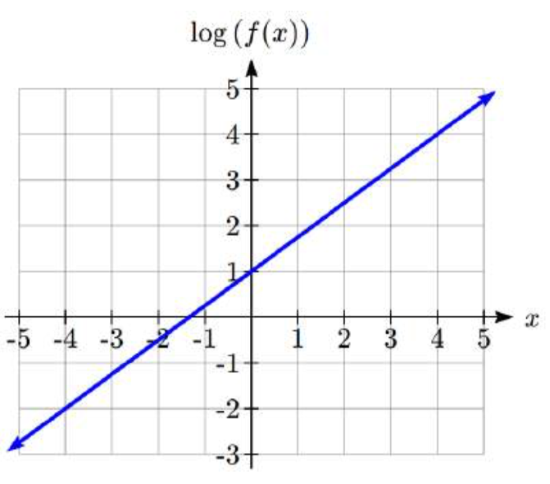
- Answer
-
g(x)=102−0.5x=102(10−0.5)x,f(x)=100(0.3162)x
Fitting Exponential Functions to Data
Some technology options provide dedicated functions for finding exponential functions that fit data, but many only provide functions for fitting linear functions to data. The semi-log scale provides us with a method to fit an exponential function to data by building upon the techniques we have for fitting linear functions to data.
to fit an exponential function to a set of data using linearization
- Find the log of the data output values
- Find the linear equation that fits the (input, log(output)) pairs. This equation will be of the form log(f(x)) = b+mx.
- Solve this equation for the exponential function f(x)
Example 4.7.4
The table below shows the cost in dollars per megabyte of storage space on computer hard drives from 1980 to 2004, and the data is shown on a standard graph to the right, with the input changed to years after 1980.
Year Cost per MB 1980192.31198487.86198815.981992419960.17320000.00684920040.001149
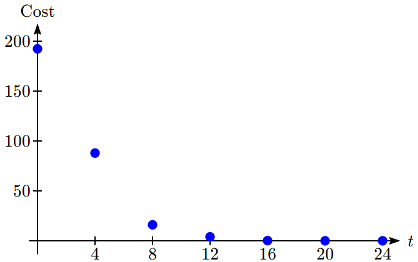
This data appears to be decreasing exponentially. To find a function that models this decay, we would start by finding the log of the costs.
Year t Cost per MB log( Cost )19800192.312.2840021984487.861.9437911988815.981.20357719921240.602061996160.173−0.761952000200.006849−2.164372004240.001149−2.93952
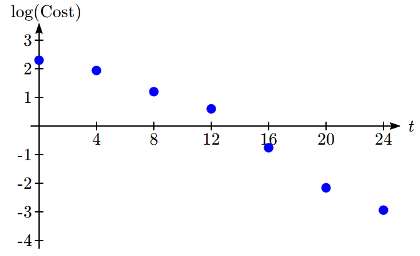
Solution
As hoped, the graph of the log of costs appears fairly linear, suggesting an exponential function will fit the original data will fit reasonably well. Using technology, we can find a linear equation to fit the log(Cost) values. Using t as years after 1980, linear regression gives the equation:
log(C(t))=2.794−0.231t
Solving for C(t),
C(t)=102.794−0.231t
C(t)=102.794⋅10−0.231t
C(t)=102.794⋅(10−0.231)t
C(t)=622⋅(0.5877)t
This equation suggests that the cost per megabyte for storage on computer hard drives is decreasing by about 41% each year.
Using this function, we could predict the cost of storage in the future. Predicting the cost in the year 2020 (t=40):
C(40)=622(0.5877)40≈0.000000364 dollars per megabyte, a really small number. That is equivalent to $0.36 per terabyte of hard drive storage.
Comparing the values predicted by this model to the actual data, we see the model matches the original data in order of magnitude, but the specific values appear quite different. This is, unfortunately, the best exponential model that can fit the data. It is possible that a non-exponential model would fit the data better, or there could just be wide enough variability in the data that no relatively simple model would fit the data any better.
| Year | Actual Cost per MB | Cost predicted by model |
| 1980 | 192.31 | 622.3 |
| 1984 | 87.86 | 74.3 |
| 1988 | 15.98 | 8.9 |
| 1992 | 4 | 1.1 |
| 1996 | 0.173 | 0.13 |
| 2000 | 0.006849 | 0.015 |
| 2004 | 0.001149 | 0.0018 |
Exercise 4.7.2
The table below shows the value V, in billions of dollars, of US imports from China t years after 2000.
| year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| t | 0 | 1 | 2 | 3 | 4 | 5 |
| V | 100 | 102.3 | 125.2 | 152.4 | 196 |
This data appears to be growing exponentially. Linearize this data and build a model to predict how many billions of dollars of imports were expected in 2011.
- Answer
-
V(t)=90.545(1.2078)t. Predicting in 2011, V(11)=722.45 billion dollars.
Important Topics of this Section
- Semi-log graph
- Log-log graph
- Linearizing exponential functions
- Fitting an exponential equation to data


