6.3E: Inverse Trigonometric Functions (Exercises)
- Page ID
- 13925
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Section 6.3 Exercises
Evaluate the following expressions, giving the answer in radians.
1. \(\sin ^{-1} \left(\dfrac{\sqrt{2} }{2} \right)\)
2. \(\sin ^{-1} \left(\dfrac{\sqrt{3} }{2} \right)\)
3. \(\sin ^{-1} \left(-\dfrac{1}{2} \right)\)
4. \(\sin ^{-1} \left(-\dfrac{\sqrt{2} }{2} \right)\)
5. \(\cos ^{-1} \left(\dfrac{1}{2} \right)\)
6. \(\cos ^{-1} \left(\dfrac{\sqrt{2} }{2} \right)\)
7. \(\cos ^{-1} \left(-\dfrac{\sqrt{2} }{2} \right)\)
8. \(\cos ^{-1} \left(-\dfrac{\sqrt{3} }{2} \right)\)
9. \(\tan ^{-1} \left(1\right)\)
10. \(\tan ^{-1} \left(\sqrt{3} \right)\)
11. \(\tan ^{-1} \left(-\sqrt{3} \right)\)
12. \(\tan ^{-1} \left(-1\right)\)
Use your calculator to evaluate each expression, giving the answer in radians.
13. \(\cos ^{-1} \left(-0.4\right)\)
14. \(\cos ^{-1} \left(0.8\right)\)
15. \(\sin ^{-1} \left(-0.8\right)\)
16. \(\tan ^{-1} \left(6\right)\)
Find the angle \(\theta\) in degrees.
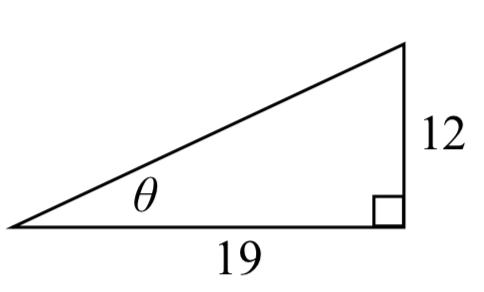
17. 
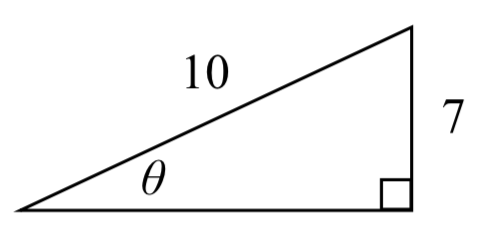18.
Evaluate the following expressions.
19. \(\sin ^{-1} \left(\cos \left(\dfrac{\pi }{4} \right)\right)\)
20. \(\cos ^{-1} \left(\sin \left(\dfrac{\pi }{6} \right)\right)\)
21. \(\sin ^{-1} \left(\cos \left(\dfrac{4\pi }{3} \right)\right)\)
22. \(\cos ^{-1} \left(\sin \left(\dfrac{5\pi }{4} \right)\right)\)
23. \(\cos \left(\sin ^{-1} \left(\dfrac{3}{7} \right)\right)\)
24. \(\sin \left(\cos ^{-1} \left(\dfrac{4}{9} \right)\right)\)
25. \(\cos \left(\tan ^{-1} \left(4\right)\right)\)
26. \(\tan \left(\sin ^{-1} \left(\dfrac{1}{3} \right)\right)\)
Find a simplified expression for each of the following.
27. \(\sin \left(\cos ^{-1} \left(\dfrac{x}{5} \right)\right)\), for \(-5\le x\le 5\)
28. \(\tan \left(\cos ^{-1} \left(\dfrac{x}{2} \right)\right)\), for \(-2\le x\le 2\)
29. \(\sin \left(\tan ^{-1} \left(3x\right)\right)\)
30. \(\cos \left(\tan ^{-1} \left(4x\right)\right)\)
- Answer
-
1. \(\dfrac{\pi}{4}\)
3. \(-\dfrac{\pi}{6}\)
5. \(\dfrac{\pi}{3}\)
7. \(\dfrac{3\pi}{4}\)
9. \(\dfrac{\pi}{4}\)
11. \(-\dfrac{\pi}{3}\)
13. 1.9823
15. -0.9273
17. \(44.427^{\circ}\)
19. \(\dfrac{\pi}{4}\)
21. \(-\dfrac{\pi}{6}\)
23. \(\dfrac{2\sqrt{10}}{7}\)
25. \(\dfrac{1}{\sqrt{17}}\)
27. \(\dfrac{\sqrt{25-x^2}}{5}\)
29. \(\dfrac{3x}{\sqrt{9x^2 + 1}}\)