8.1.1: Non-Right Triangles - Laws of Sines and Cosines (Exercises)
- Page ID
- 22234
section 8.1 exercises
Solve for the unknown sides and angles of the triangles shown.
1. 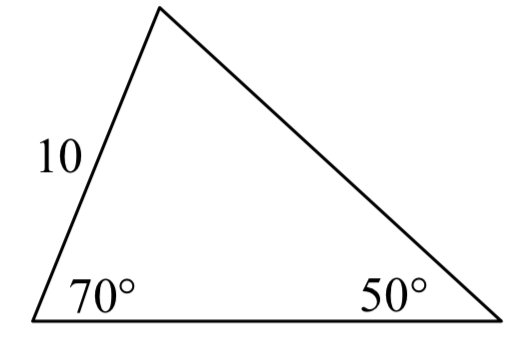 2.
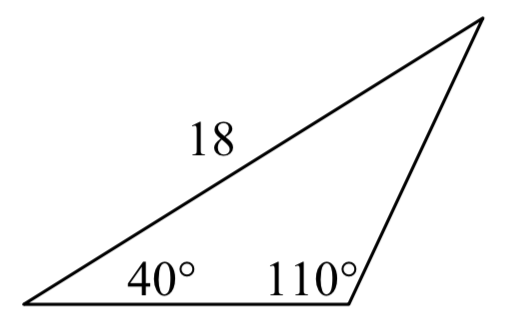
2. 
3. 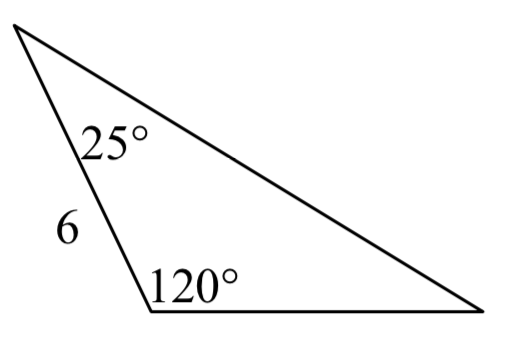 4.
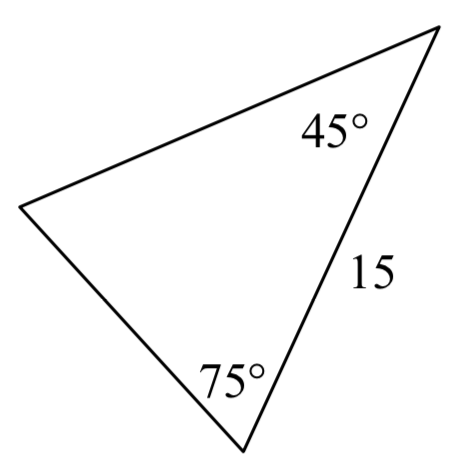
4. 
5. 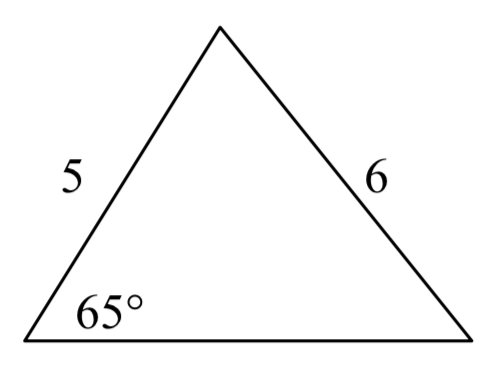 6.
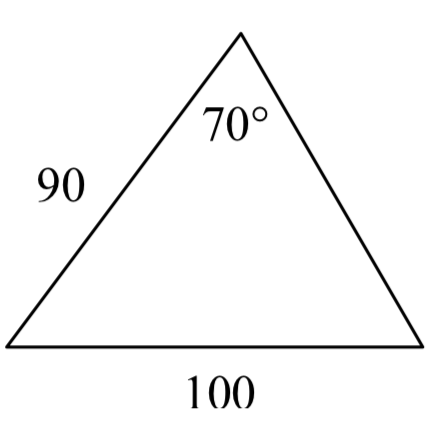
6. 
7. 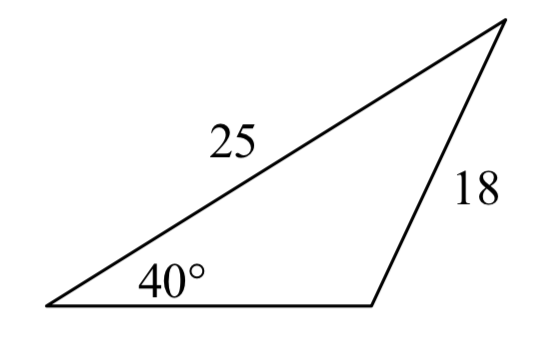 8.
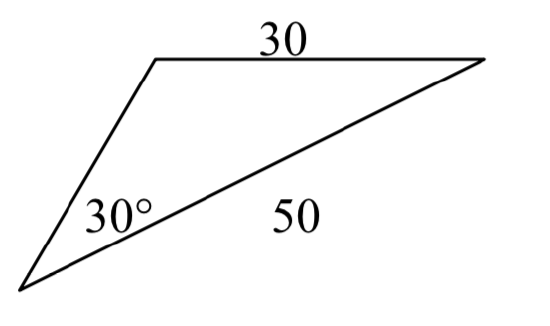
8. 
Assume \(\alpha\) is opposite side \(a\), \(\beta\) is opposite side \(b\), and \(\gamma\) is opposite side \(c\). Solve each triangle for the unknown sides and angles if possible. If there is more than one possible solution, give both.
9. \(\alpha = 43^{\circ}\), \(\gamma = 69^{circ}\), \(b = 20\)
10. \(\alpha = 35^{\circ}\), \(\gamma = 73^{circ}\), \(b = 19\)
11. \(\alpha = 119^{\circ}\), \(a = 26\), \(b = 14\)
12. \(\gamma = 113^{circ}\), \(b = 10\), \(c = 32\)
13. \(\beta = 50^{circ}\), \(a = 105\), \(b = 45\)
14. \(\beta = 67^{circ}\), \(a = 49\), \(b = 38\)
15. \(\alpha = 43.1^{circ}\), \(a = 184.2\), \(b = 242.8\)
16. \(\alpha = 36.6^{\circ}\), \(a = 186.2\), \(b = 242.2\)
Solve for the unknown sides and angles of the triangles shown.
17. 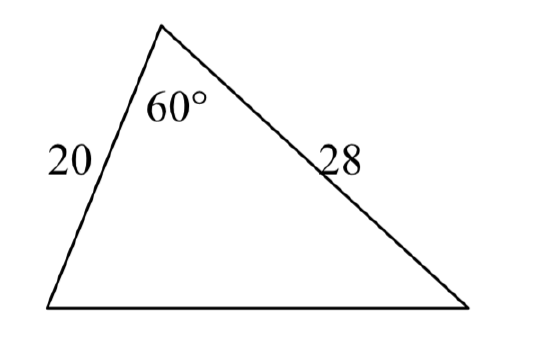 18.
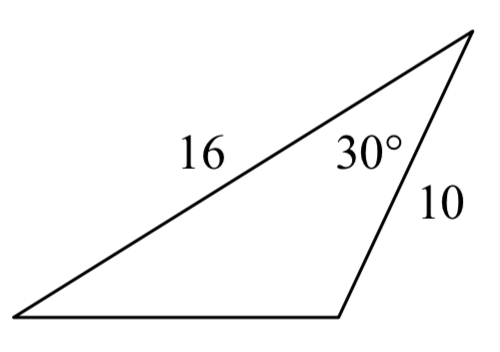
18. 
19.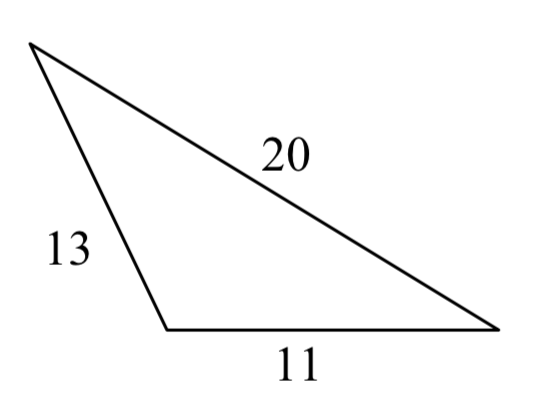 20.
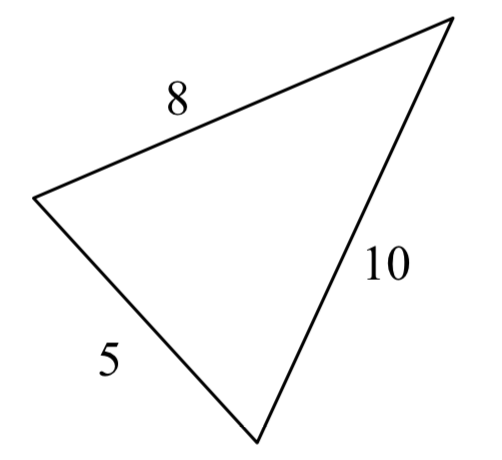
20. 
Assume \(\alpha\) is opposite side \(a\), \(\beta\) is opposite side \(b\), and \(\gamma\) is opposite side \(c\). Solve each triangle for the unknown sides and angles if possible. If there is more than one possible solution, give both.
21. \(\gamma = 41.2^{\circ}\), \(a = 2.49\), \(b = 3.13\)
22. \(\beta = 58.7^{\circ}\), \(a = 10.6\), \(c = 15.7\)
23. \(\alpha = 120^{\circ}\), \(b = 6\), \(c = 7\)
24. \(\gamma = 115^{\circ}\), \(a = 18\), \(b = 23\)
25. Find the area of a triangle with sides of length 18, 21, and 32.
26. Find the area of a triangle with sides of length 20, 26, and 37.
27. To find the distance across a small lake, a surveyor has taken the measurements shown. Find the distance across the lake.
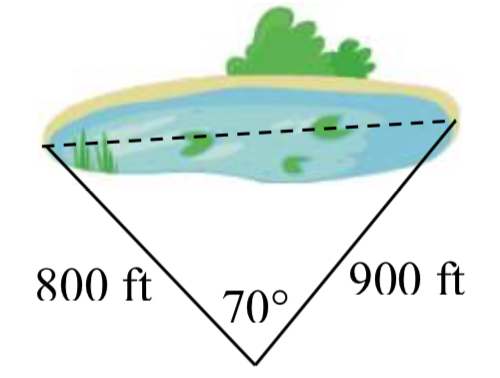
28. To find the distance between two cities, a satellite calculates the distances and angle shown (\(not to scale\)). Find the distance between the cities.
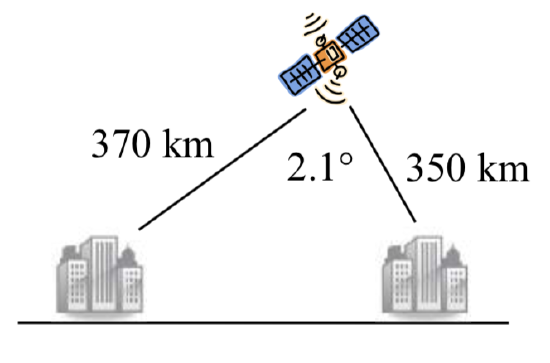
29. o determine how far a boat is from shore, two radar stations 500 feet apart determine the angles out to the boat, as shown. Find the distance of the boat from the station A, and the distance of the boat from shore.
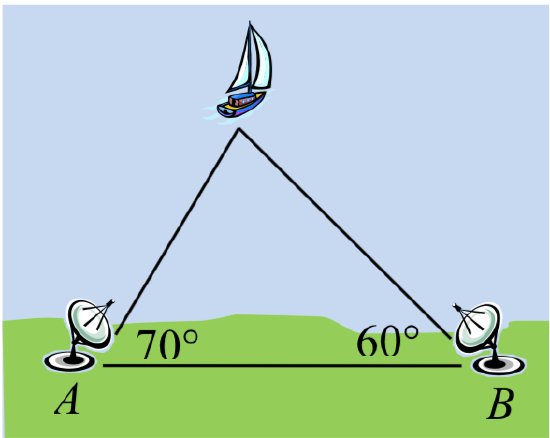
30. The path of a satellite orbiting the earth causes it to pass directly over two tracking stations \(A\) and \(B\), which are 69 mi apart. When the satellite is on one side of the two stations, the angles of elevation at \(A\) and \(B\) are measured to be \(86.2^{\circ}\) and \(83.9^{\circ}\), respectively. How far is the satellite from station \(A\) and how high is the satellite above the ground?
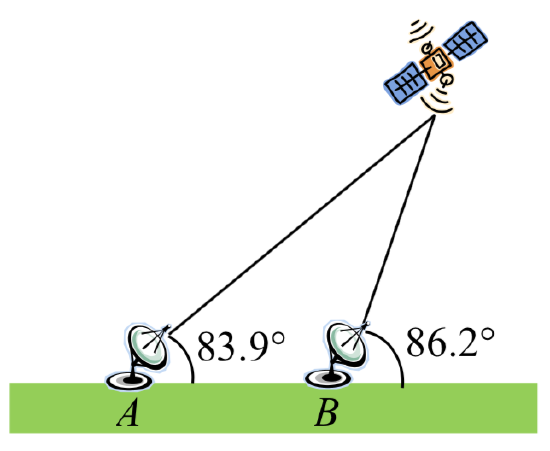
31. A communications tower is located at the top of a steep hill, as shown. The angle of inclination of the hill is \(67^{\circ}\). A guy-wire is to be attached to the top of the tower and to the ground, 165 m downhill from the base of the tower. The angle formed by the guy-wire and the hill is \(16^{\circ}\). Find the length of the cable required for the guy wire.
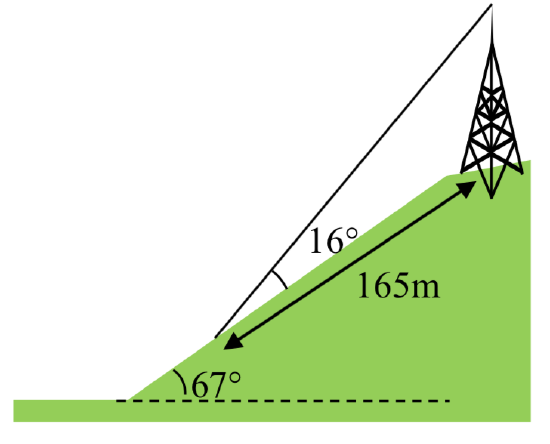
32. The roof of a house is at a \(20^{\circ}\) angle. An 8 foot solar panel is to be mounted on the roof, and should be angled \(38^{\circ}\) relative to the horizontal for optimal results. How long does the vertical support holding up the back of the panel need to be?
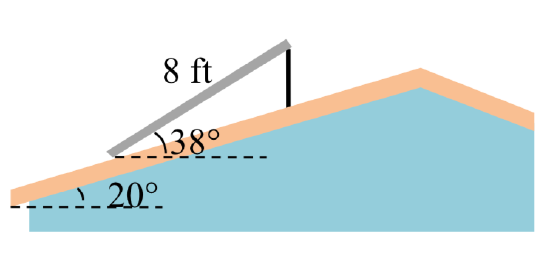
33. A 127 foot tower is located on a hill that is inclined \(38^{\circ}\) to the horizontal. A guy-wire is to be attached to the top of the tower and anchored at a point 64 feet downhill from the base of the tower. Find the length of wire needed.
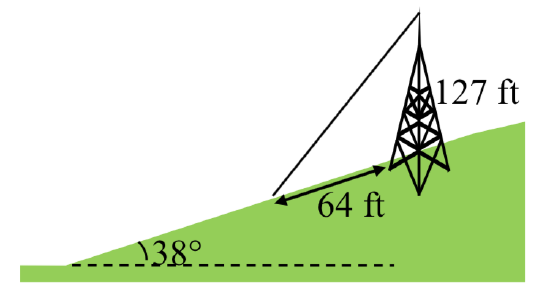
34. A 113 foot tower is located on a hill that is inclined \(34^{\circ}\) to the horizontal. A guy-wire is to be attached to the top of the tower and anchored at a point 98 feet uphill from the base of the tower. Find the length of wire needed.
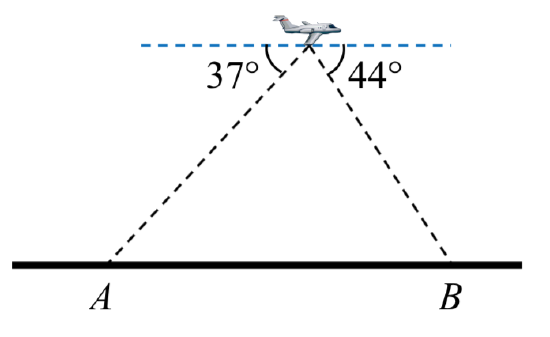
35. A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 6.6 km apart, to be \(37^{\circ}\) and \(44^{\circ}\), as shown in the figure. Find the distance of the plane from point \(A\), and the elevation of the plane.
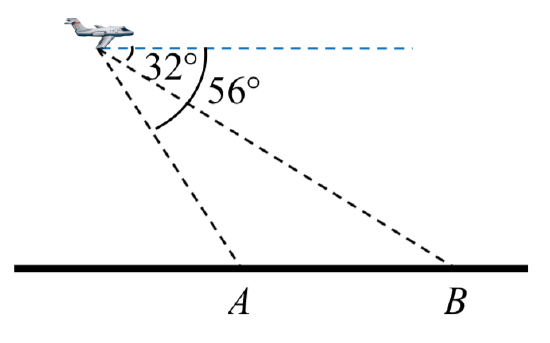
36. A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 4.3 km apart, to be \(32^{\circ}\) and \(56^{\circ}\), as shown in the figure. Find the distance of the plane from point \(A\), and the elevation of the plane.
37. To estimate the height of a building, two students find the angle of elevation from a point (at ground level) down the street from the building to the top of the building is \(39^{\circ}\). From a point that is 300 feet closer to the building, the angle of elevation (at ground level) to the top of the building is \(50^{\circ}\). If we assume that the street is level, use this information to estimate the height of the building.
38. To estimate the height of a building, two students find the angle of elevation from a point (at ground level) down the street from the building to the top of the building is \(35^{\circ}\). From a point that is 300 feet closer to the building, the angle of elevation (at ground level) to the top of the building is \(53^{\circ}\). If we assume that the street is level, use this information to estimate the height of the building.
39. A pilot flies in a straight path for 1 hour 30 min. She then makes a course correction, heading 10 degrees to the right of her original course, and flies 2 hours in the new direction. If she maintains a constant speed of 680 miles per hour, how far is she from her starting position?
40. Two planes leave the same airport at the same time. One flies at 20 degrees east of north at 500 miles per hour. The second flies at 30 east of south at 600 miles per hour. How far apart are the planes after 2 hours?
41. The four sequential sides of a quadrilateral have lengths 4.5 cm, 7.9 cm, 9.4 cm, and 12.9 cm. The angle between the two smallest sides is \(117^{\circ}\). What is the area of this quadrilateral?
42. The four sequential sides of a quadrilateral have lengths 5.7 cm, 7.2 cm, 9.4 cm, and 12.8 cm. The angle between the two smallest sides is \(106^{\circ}\). What is the area of this quadrilateral?
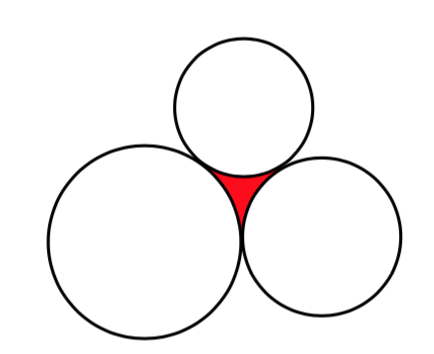
43. Three circles with radii 6, 7, and 8, all touch as shown. Find the shaded area bounded by the three circles.
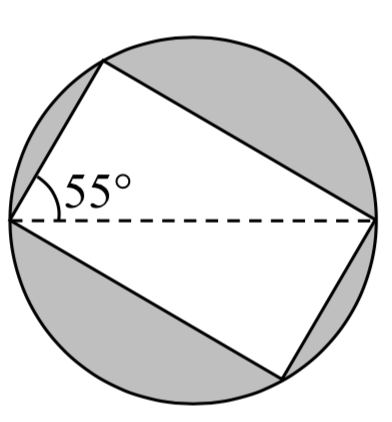
44. A rectangle is inscribed in a circle of radius 10 cm as shown. Find the shaded area, inside the circle but outside the rectangle.
- Answer
-
1.
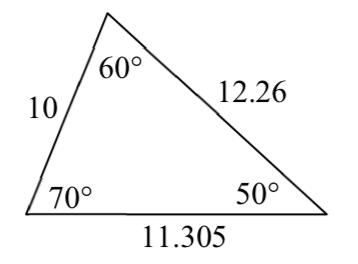
3.
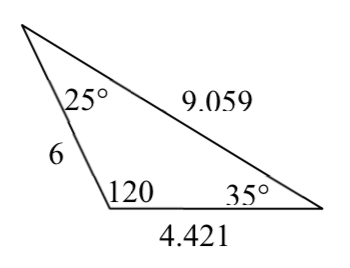
5.
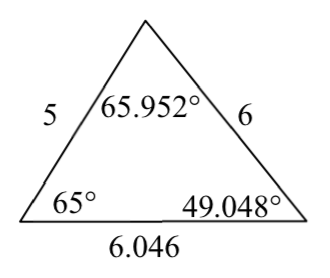
7.
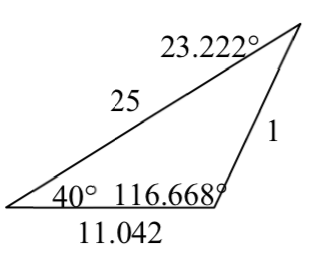
9. \(\beta = 68^(\circ)\), \(a = 14.711\), \(c = 20.138\)
11. \(\beta = 28.096^(\circ)\), \(\gamma = 32.904^(\circ)\), \(c = 16.149\)
13. Not possible.
15. \(\beta = 64.243^(\circ)\), \(\gamma = 72.657^(\circ)\), \(c = 257.328\) OR \(\beta = 115.757^(\circ)\), \(\gamma = 21.143^(\circ)\), \(c = 97.238\)
17.
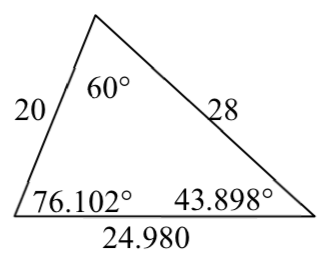
19.
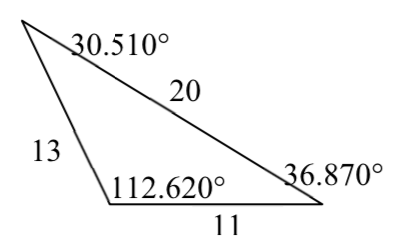
21. \(c = 2.066\), \(\alpha = 52.545^(\circ)\), \(\beta = 86.255^(\circ)\)
23. \(\alpha = 11.269\), \(\beta = 27.457^(\circ)\), \(\gamma = 32.543^(\circ)\)
25. 177.562
27. 978.515 ft
29. Distance to A: 565.258ft. Distance to shore: 531.169 ft
31. 529.014
33. 173.877 feet
35. 4.642 km, 2.794 km
37. 757.963 ft
39. 2371.129 miles
41. 65.375 cm\(^(2)\)
43. 7.72


