9.3: Parabolas and Non-Linear Systems

To listen for signals from space, a radio telescope uses a dish in the shape of a parabola to focus and collect the signals in the receiver.

While we studied parabolas earlier when we explored quadratics, at the time we did not discuss them as a conic section. A parabola is the shape resulting from when a plane parallel to the side of the cone intersects the cone (Pbroks13 (commons.wikimedia.org/wiki/F...with_plane.svg), “Conic sections with plane”, cropped to show only parabola, CC BY 3.0).

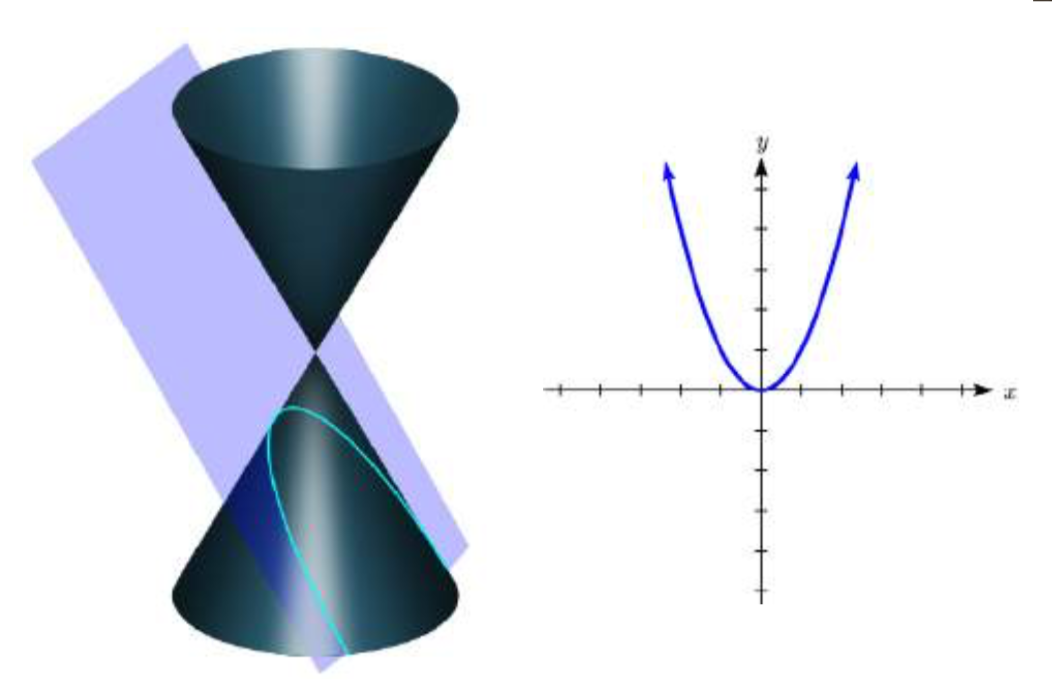
Definition: PARABOLA Definition AND VOCABULARY

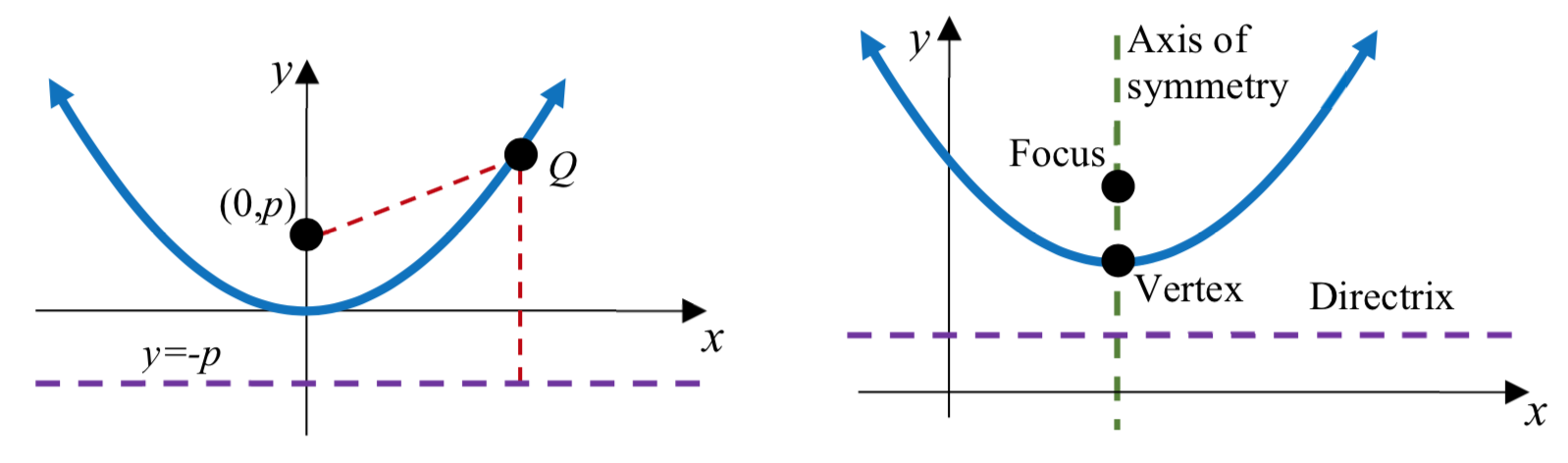
A parabola with vertex at the origin can be defined by placing a fixed point at $F\left( 0,p \right)$ called the focus, and drawing a line at $y = - p$, called the directrix. The parabola is the set of all points $Q\left( x,y \right)$ that are an equal distance between the fixed point and the directrix.

For general parabolas,
The axis of symmetry is the line passing through the foci, perpendicular to the directrix.
The vertex is the point where the parabola crosses the axis of symmetry.
The distance from the vertex to the focus, $p$, is the focal length.

Equations for Parabolas with Vertex at the Origin

From the definition above we can find an equation of a parabola. We will find it for a parabola with vertex at the origin, $C\left( 0,0 \right)$, opening upward with focus at $F\left( 0,p \right)$ and directrix at $y = - p$.

Suppose$Q\left( x,y \right)$ is some point on the parabola. The distance from $Q$ to the focus is

$$d(Q,F)=\sqrt{(x-0)^{2}+(y-p)^{2}}=\sqrt{x^{2}+(y-p)^{2}}\nonumber$$

The distance from the point $Q$ to the directrix is the difference of the $y$-values:

$$d = y - ( - p) = y + p\nonumber$$

From the definition of the parabola, these distances should be equal:

$$\sqrt {x^2 + \left( y - p \right)^2} = y + p\nonumber$$ Square both sides
$$x^2 + \left( y - p \right)^2 = \left( y + p \right)^2\nonumber$$ Expand
$$x^2 + y^2 - 2py + p^2 = y^2 + 2py +p^2\nonumber$$ Combine like terms
$$x^2 = 4py\nonumber$$

This is the standard conic form of a parabola that opens up or down (vertical axis of symmetry), centered at the origin. Note that if we divided by $4p$, we would get a more familiar equation for the parabola, $y = \dfrac{x^2}{4p}$. We can recognize this as a transformation of the parabola $y = x^2$, vertically compressed or stretched by $\dfrac{1}{4p}$.

Using a similar process, we could find an equation of a parabola with vertex at the origin opening left or right. The focus will be at ($p$,0) and the graph will have a horizontal axis of symmetry and a vertical directrix. The standard conic form of its equation will be $y^2 = 4px$, which we could also write as $x = \dfrac{y^2}{4p}$.

Example $\PageIndex{1}$

Write the standard conic equation for a parabola with vertex at the origin and focus at (0, -2).

Solution

With focus at (0, -2), the axis of symmetry is vertical, so the standard conic equation is $x^2 = 4py$. Since the focus is (0, -2), $p = -2$.

The standard conic equation for the parabola is $$x^2 = 4( - 2)y\text{, or }x^2 = - 8y\nonumber$$
For parabolas with vertex not at the origin, we can shift these equations, leading to the equations summarized next.

EQUATION OF A PARABOLA WITH VERTEX AT $h,k$ IN STANDARD CONIC FORM

The standard conic form of an equation of a parabola with vertex at the point $\left( h,k \right)$ depends on whether the axis of symmetry is horizontal or vertical. The table below gives the standard equation, vertex, axis of symmetry, directrix, focus, and graph for each.

	Horizontal	Vertical
Standard Equation	$(y - k)^2 = 4p(x - h)$	$(x - h)^2 = 4p(y - k)$
Vertex	$(h, k)$	$(h, k)$
Axis of symmetry	$y = k$	$x = h$
Directrix	$x = h - p$	$y = k - p$
Focus	$(h +p, k)$	$(h, k + p)$
Graph	An example with $p < 0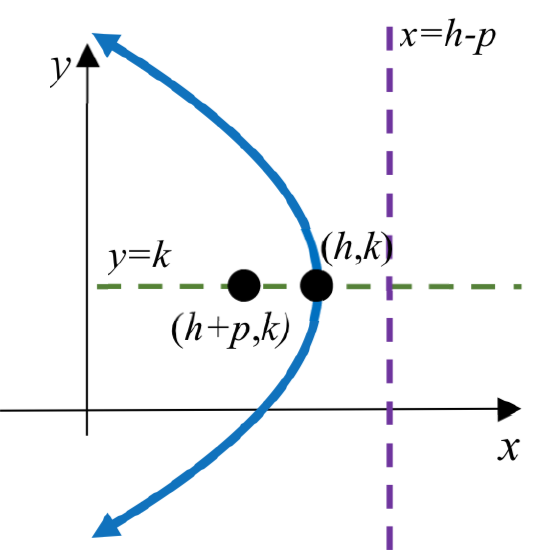$	An example with $p > 0$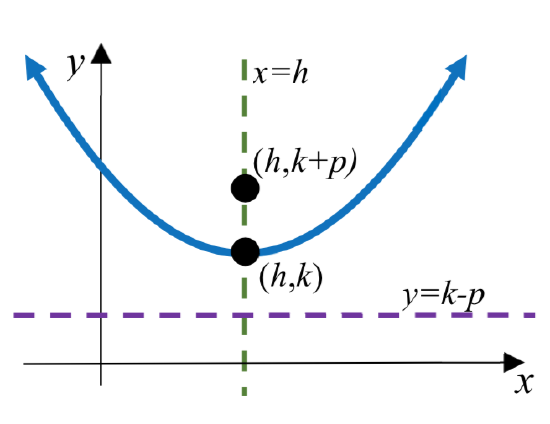

Since you already studied quadratics in some depth earlier, we will primarily explore the new concepts associated with parabolas, particularly the focus.

Example $\PageIndex{2}$

Put the equation of the parabola $y = 8{(x - 1)^2} + 2$ in standard conic form. Find the vertex, focus, and axis of symmetry.

Solution

From your earlier work with quadratics, you may already be able to identify the vertex as (1,2), but we’ll go ahead and put the parabola in the standard conic form. To do so, we need to isolate the squared factor.

$$y = 8(x - 1)^2 + 2\nonumber$$ Subtract 2 from both sides
$$y - 2 = 8(x - 1)^2\nonumber$$ Divide by 8
$$\dfrac{\left( y - 2 \right)}{8} = (x - 1)^2\nonumber$$

This matches the general form for a vertical parabola, $\left( x - h \right)^2 = 4p\left( y - k \right)$, where $4p = \dfrac{1}{8}$. Solving this tells us $p = \dfrac{1}{32}$. The standard conic form of the equation is

$$\left( x - 1 \right)^2 = 4\left( \dfrac{1}{32} \right)\left( y - 2 \right). \nonumber$$

The vertex is at (1,2). The axis of symmetry is at $x = 1$.
The directrix is at $$y = 2 - \dfrac{1}{32} = \dfrac{63}{32}\nonumber$$
The focus is at $$\left( 1,2 + \dfrac{1}{32} \right) = \left( 1,\dfrac{65}{32} \right)\nonumber$$

Example $\PageIndex{3}$

A parabola has its vertex at (1, 5) and focus at (3, 5). Find an equation for the parabola.

Solution

Since the vertex and focus lie on the line $y = 5$, that is our axis of symmetry.

The vertex (1, 5) tells us $h = 1$ and $k = 5$.

Looking at the distance from the vertex to the focus, $p = 3 – 1 = 2$.

Substituting these values into the standard conic form of an equation for a horizontal parabola gives the equation

$$\left( y - 5 \right)^2 = 4(2)\left( x - 1 \right)\nonumber$$

$$\left( y - 5 \right)^2 = 8\left( x - 1 \right)\nonumber$$

Note this could also be rewritten by solving for $x$, resulting in

$$x = \dfrac{1}{8}{\left( {y - 5} \right)^2} + 1\nonumber$$

Exercise $\PageIndex{1}$

A parabola has its vertex at (-2,3) and focus at (-2,2). Find an equation for this parabola.

Answer

Axis of symmetry is vertical, and the focus is below the vertex.
$$p = 2 – 3 = -1\nonumber$$
$$\left( x - ( - 2) \right)^2 = 4( - 1)\left( y - 3 \right)\text{, or }\left( x + 2 \right)^2 = - 4\left( y - 3 \right)\nonumber$$

Applications of Parabolas

In an earlier section, we learned that ellipses have a special property that a ray emanating from one focus will be reflected back to the 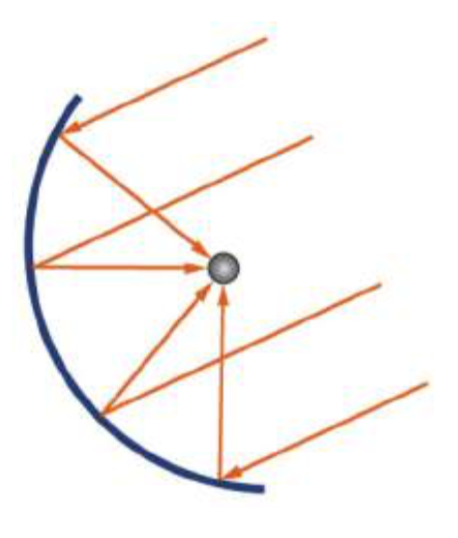other focus, the property that enables the whispering chamber to work. Parabolas also have a special property, that any ray emanating from the focus will be reflected parallel to the axis of symmetry. Reflectors in flashlights take advantage of this property to focus the light from the bulb into a collimated beam. The same property can be used in reverse, taking parallel rays of sunlight or radio signals and directing them all to the focus.

Example $\PageIndex{4}$

A solar cooker is a parabolic dish that reflects the sun’s rays to a central point allowing you to cook food. If a solar cooker has a parabolic dish 16 inches in diameter and 4 inches tall, where should the food be placed?

Solution

We need to determine the location of the focus, since that’s where the food should be placed. Positioning th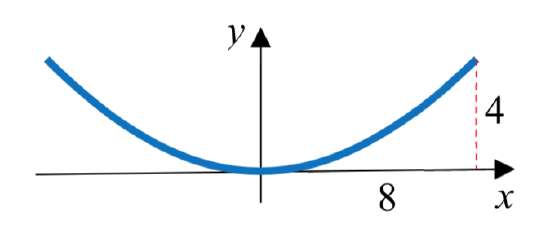e base of the dish at the origin, the shape from the side looks like:

The standard conic form of an equation for the parabola would be ${x^2} = 4py$. The parabola passes through (4, 8), so substituting that into the equation, we can solve for $p$:

$$8^2 = 4(p)(4)\nonumber$$
$$p = \dfrac{8^2}{16} = 4\nonumber$$

The focus is 4 inches above the vertex. This makes for a very convenient design, since then a grate could be placed on top of the dish to hold the food.

Exercise $\PageIndex{2}$

A radio telescope is 100 meters in diameter and 20 meters deep. Where should the receiver be placed?

Answer

The standard conic form of the equation is $$x^2 = 4py\nonumber$$
Using (50,20), we can find that $50^2 = 4p(20)$, so $p = 31.25$ meters.
The receiver should be placed 31.25 meters above the vertex.

Non-Linear Systems of Equations

In many applications, it is necessary to solve for the intersection of two curves. Many of the techniques you may have used before to solve systems of linear equations will work for non-linear equations as well, particularly substitution. You have already solved some examples of non-linear systems when you found the intersection of a parabola and line while studying quadratics, and when you found the intersection of a circle and line while studying circles.

Example $\PageIndex{4}$

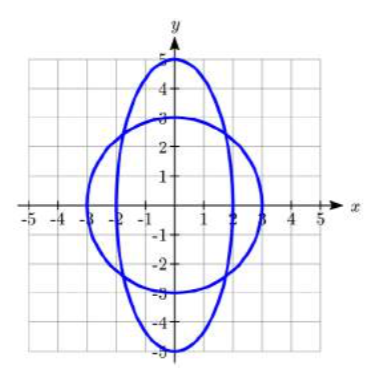
Find the points where the ellipse $\dfrac{x^2}{4} + \dfrac{y^2}{25} = 1$ intersects the circle $x^2+ y^2 = 9$.

Solution

To start, we might multiply the ellipse equation by 100 on both sides to clear the fractions, giving $$25x^2 + 4y^2 = 100\nonumber$$

A common approach for finding intersections is substitution. With these equations, rather than solving for $x$ or $y$, it might be easier to solve for $x^2$ or $y^2$. Solving the circle equation for $x^2$ gives $x^2 = 9 - y^2$. We can then substitute that expression for $x^2$ into the ellipse equation.

$$25x^2 + 4y^2= 100\nonumber$$ Substitute $x^2 = 9 - y^2$
$$25\left( 9 - y^2 \right) + 4y^2 = 100\nonumber$$ Distribute
$$225 - 25y^2 + 4y^2 = 100\nonumber$$ Combine like terms
$$- 21y^2 = - 125\nonumber$$ Divide by -21
$$y^2 = \dfrac{125}{21}\nonumber$$ Use the square root to solve
$$y = \pm \sqrt {\dfrac{125}{21}} = \pm \dfrac{5\sqrt 5 }{\sqrt {21} }\nonumber$$

We can substitute each of these $y$ values back in to $x^2 = 9 - y^2$ to find $x$

$$x^{2}=9-\left(\sqrt{\frac{125}{21}} \right)^{2}=9-\frac{125}{21}=\frac{189}{21}-\frac{125}{21}=\frac{64}{21}\nonumber$$

$$x = \pm \sqrt {\dfrac{64}{21}} = \pm \dfrac{8}{\sqrt {21} }\nonumber$$

There are four points of intersection: $$\left( \pm \dfrac{8}{\sqrt {21} }, \pm \dfrac{5\sqrt 5 }{\sqrt {21} } \right)\nonumber$$

It’s worth noting there is a second technique we could have used in the previous example, called elimination. If we multiplied the circle equation by -4 to get $- 4x^2 - 4y^2 = - 36$, we can then add it to the ellipse equation, eliminating the variable $y$.

$$25x^2 + 4y^2 = 100\nonumber$$
$$- 4x^2 - 4y^2 = - 36\nonumber$$ Add the left sides, and add the right sides
$$21x^2 = 64\nonumber$$ Solve for $x$
$$x = \pm \sqrt {\dfrac{64}{21}} = \pm \dfrac{8}{\sqrt {21} }\nonumber$$

Example $\PageIndex{5}$

Find the points where the hyperbola $\dfrac{y^2}{4} - \dfrac{x^2}{9} = 1$ intersects the parabola $y = 2x^2$.

Solution

We can solve this system of equations by substituting $y = 2{x^2}$ into the hyperbola equation.

$$\dfrac{(2x^2)^2}{4} - \dfrac{x^2}{9} = 1\nonumber$$ Simplify
$$\dfrac{4x^4}{4} - \dfrac{x^2}{9} = 1\nonumber$$ Simplify, and multiply by 9
$$9x^4 - x^2 = 9\nonumber$$ Move the 9 to the left
$$9x^4 - x^2 - 9 = 0\nonumber$$

While this looks challenging to solve, we can think of it as a “quadratic in disguise,” since $x^4 = (x^2)^2$. Letting $u = x^2$, the equation becomes

$$9u^2 - u^2 - 9 = 0\nonumber$$ Solve using the quadratic formula
$$u = \dfrac{ - ( - 1) \pm \sqrt ( - 1)^2 - 4(9)( - 9) }{2(9)} = \dfrac{1 \pm \sqrt {325} }{18}\nonumber$$ Solve for $x$
$$x^2 = \dfrac{1 \pm \sqrt {325} }{18}\nonumber$$ But $1 - \sqrt {325} < 0$, so
$$x = \pm \sqrt {\dfrac{1 + \sqrt {325} }{18}} \nonumber$$ This leads to two real solutions
$$x \approx 1.028, -1.028\nonumber$$

Substituting these into $y = 2{x^2}$, we can find the corresponding y values.
The curves intersect at the points (1.028, 2.114) and (-1.028, 2.114).

Exercise $\PageIndex{3}$

Find the points where the line $y = 4x$ intersect the ellipse $\dfrac{y^2}{4} - \dfrac{x^2}{16} = 1$

Answer

Substituting $y = 4x$ gives $\dfrac{\left( 4x \right)^2}{4} - \dfrac{x^2}{16} = 1$.
Simplify
$$\dfrac{16x^2}{4} - \dfrac{x^2}{16} = 1\nonumber$$ Multiply by 16 to get
$$64x^2 - x^2 = 16\nonumber$$
$$x = \pm \sqrt {\dfrac{16}{63}} = \pm 0.504\nonumber$$

Substituting those into $y = 4x$ gives the corresponding $y$ values.
The curves intersect at (0.504, 2.016) and (-0.504, -2.016).

Solving for the intersection of two hyperbolas allows us to utilize the LORAN navigation approach descr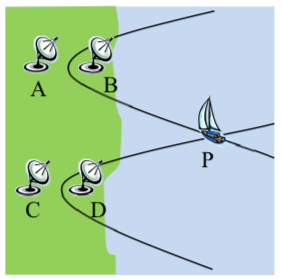ibed in the last section.

In our example, stations A and B are 150 kilometers apart and send a simultaneous radio signal to the ship. The signal from B arrives 0.0003 seconds before the signal from A. We found the equation of the hyperbola in standard form would be

$$\dfrac{x^2}{2025} - \dfrac{y^2}{3600} = 1\nonumber$$

Example $\PageIndex{10}$

Continuing the situation from the last section, suppose stations C and D are located 200 km due south of stations A and B and 100 km apart. The signal from D arrives 0.0001 seconds before the signal from C, leading to the equation $\dfrac{x^2}{225} - \dfrac{(y + 200)^2}{2275} = 1$. Find the position of the ship.

Solution

To solve for the position of the boat, we need to find where the hyperbolas intersect. This means solving the system of equations. To do this, we could start by solving both equations for ${x^2}$. With the first equation from the previous example

$$\dfrac{x^2}{2025} - \dfrac{y^2}{3600} = 1\nonumber$$ Move the $y$ term to the right
$$\dfrac{x^2}{2025} = 1 + \dfrac{y^2}{3600}\nonumber$$ Multiply both sides by 2025
$$x^2 = 2025 + \dfrac{2025y^2}{3600}\nonumber$$ Simplify
$$x^2 = 2025 + \dfrac{9y^2}{16}\nonumber$$

With the second equation, we repeat the same process

$$\dfrac{x^2}{225} - \dfrac{(y + 200)^2}{2275} = 1\nonumber$$ Move the $y$ term to the right and multiply by 225
$$x^2 = 225 + \dfrac{225(y + 200)^2}{2275}\nonumber$$ Simplify
$$x^2 = 225 + \dfrac{9(y + 200)^2}{91}\nonumber$$

Now set these two expressions for $x^2$ equal to each other and solve.

$$2025 + \dfrac{9y^2}{16} = 225 + \dfrac{9(y + 200)^2}{91}\nonumber$$ Subtract 225 from both sides
$$1800 + \dfrac{9y^2}{16} = \dfrac{9(y + 200)^2}{91}\nonumber$$ Divide by 9
$$200 + \dfrac{y^2}{16} = \dfrac{(y + 200)^2}{91}\nonumber$$ Multiply both sides by $16 \cdot 91 = 1456$
$$291200 + 91y^2 = 16(y + 200)^2\nonumber$$ Expand and distribute
$$291200 + 91y^2 = 16y^2 + 6400y + 640000\nonumber$$ Combine like terms on one side
$$75y^2 - 6400y - 348800 = 0\nonumber$$ Solve using the quadratic formula
$$y = \dfrac{ - ( - 6400) \pm \sqrt {( - 6400)^2 - 4(75)( - 348800)} }{2(75)} \approx 123.11 \text{ km or }-37.78\text{ km}\nonumber$$

We can find the associated $x$ values by substituting these $y$-values into either hyperbola equation. When $y \approx 123.11$,

$$x^2 \approx 2025 + \dfrac{9(123.11)^2}{16}\nonumber$$
$$x \approx \pm 102.71\nonumber$$

When $y \approx$ -37.78 km,

$$x^2 \approx 2025 + \dfrac{9( - 37.78)^2}{16}\nonumber$$
$$x \approx \pm 53.18\nonumber$$

This provides 4 possible locations for the ship. Two can be immediately discarded, as they’re on land. Navigators would use other navigational techniques to decide between the two remaining locations.

Important Topics of This Section

• Parabola Definition
• Parabola Equations in Standard Form
• Applications of Parabolas
• Solving Non-Linear Systems of Equations