1.1: The Unit Circle
- Page ID
- 7097
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- What is the unit circle and why is it important in trigonometry? What is the equation for the unit circle?
- What is meant by “wrapping the number line around the unit circle?” How is this used to identify real numbers as the lengths of arcs on the unit circle?
- How do we associate an arc on the unit circle with a closed interval of real numbers?
Beginning Activity
As has been indicated, one of the primary reasons we study the trigonometric functions is to be able to model periodic phenomena mathematically. Before we begin our mathematical study of periodic phenomena, here is a little “thought experiment” to consider.
Imagine you are standing at a point on a circle and you begin walking around the circle at a constant rate in the counterclockwise direction. Also assume that it takes you four minutes to walk completely around the circle one time. Now suppose you are at a point \(P\) on this circle at a particular time \(t\).
- Describe your position on the circle \(2\) minutes after the time \(t\).
- Describe your position on the circle \(4\) minutes after the time \(t\).
- Describe your position on the circle \(6\) minutes after the time \(t\).
- Describe your position on the circle \(8\) minutes after the time \(t\).
The idea here is that your position on the circle repeats every \(4\) minutes. After \(2\) minutes, you are at a point diametrically opposed from the point you started. After \(4\) minutes, you are back at your starting point. In fact, you will be back at your starting point after \(8\) minutes, \(12\) minutes, \(16\) minutes, and so on. This is the idea of periodic behavior.
The Unit Circle and the Wrapping Function
In order to model periodic phenomena mathematically, we will need functions that are themselves periodic. In other words, we look for functions whose values repeat in regular and recognizable patterns. Familiar functions like polynomials and exponential functions do not exhibit periodic behavior, so we turn to the trigonometric functions. Before we can define these functions, however, we need a way to introduce periodicity. We do so in a manner similar to the thought experiment, but we also use mathematical objects and equations. The primary tool is something called the wrapping function. Instead of using any circle, we will use the so-called unit circle. This is the circle whose center is at the origin and whose radius is equal to \(1\), and the equation for the unit circle is \(x^{2}+y^{2} = 1\).
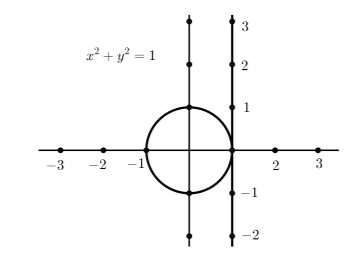
Figure \(\PageIndex{1}\): Setting up to wrap the number line around the unit circle
Figure \(\PageIndex{1}\) shows the unit circle with a number line drawn tangent to the circle at the point \((1, 0)\). We will “wrap” this number line around the unit circle. Unlike the number line, the length once around the unit circle is finite. (Remember that the formula for the circumference of a circle as \(2\pi r\) where \(r\) is the radius, so the length once around the unit circle is \(2\pi\). However, we can still measure distances and locate the points on the number line on the unit circle by wrapping the number line around the circle. We wrap the positive part of this number line around the circumference of the circle in a counterclockwise fashion and wrap the negative part of the number line around the circumference of the unit circle in a clockwise direction.
Two snapshots of an animation of this process for the counterclockwise wrap are shown in Figure \(\PageIndex{2}\) and two such snapshots are shown in Figure \(\PageIndex{3}\) for the clockwise wrap.
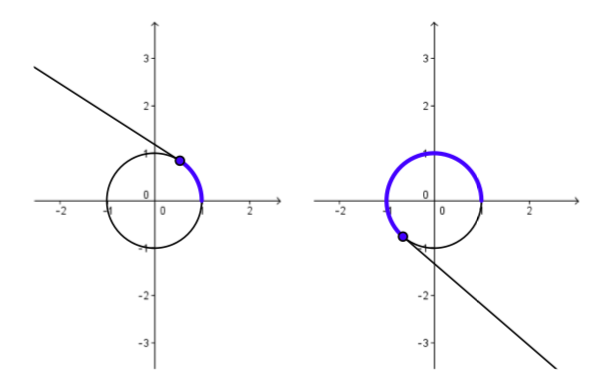
Figure \(\PageIndex{2}\): Wrapping the positive number line around the unit circle
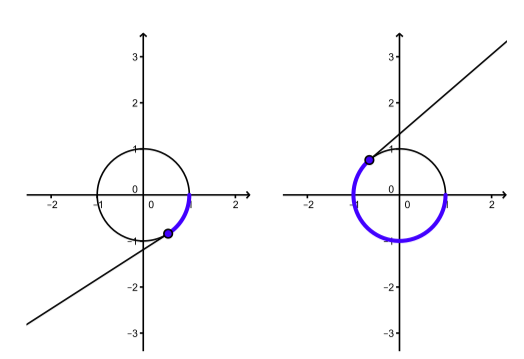
Figure \(\PageIndex{3}\): Wrapping the negative number line around the unit circle
Following is a link to an actual animation of this process, including both positive wraps and negative wraps.
Figures \(\PageIndex{2}\) and \(\PageIndex{3}\) only show a portion of the number line being wrapped around the circle. Since the number line is infinitely long, it will wrap around the circle infinitely many times. A result of this is that infinitely many different numbers from the number line get wrapped to the same location on the unit circle.
- The number 0 and the numbers \(2\pi\), \(-2\pi\), and \(4\pi\) (as well as others) get wrapped to the point \((1, 0)\). We will usually say that these points get mapped to the point \((1, 0)\).
- The number \(\pi /2\) is mapped to the point \((0, 1)\). This is because the circumference of the unit circle is \(2\pi\) and so one-fourth of the circumference is \(\frac{1}{4}(2\pi) = \pi/2\).
- If we now add \(2\pi\) to \(\pi/2\), we see that \(5\pi/2\)also gets mapped to \((0, 1)\). If we subtract \(2\pi\) from \(\pi/2\), we see that \(-3\pi/2\) also gets mapped to \((0, 1)\).
However, the fact that infinitely many different numbers from the number line get wrapped to the same location on the unit circle turns out to be very helpful as it will allow us to model and represent behavior that repeats or is periodic in nature.
Exercise \(\PageIndex{1}\)
- Find two different numbers, one positive and one negative, from the number line that get wrapped to the point \((-1, 0)\) on the unit circle.
- Describe all of the numbers on the number line that get wrapped to the point \((-1, 0)\) on the unit circle.
- Find two different numbers, one positive and one negative, from the number line that get wrapped to the point \((0, 1)\) on the unit circle.
- Find two different numbers, one positive and one negative, from the number line that get wrapped to the point \((0, -1)\) on the unit circle.
- Answer
-
Some positive numbers that are wrapped to the point \((-1, 0)\) are \(\pi, 3\pi, 5\pi\). Some negative numbers that are wrapped to the point \((-1, 0)\) are \(-\pi, -3\pi, -5\pi\).
The numbers that get wrapped to \((-1, 0)\) are the odd integer multiples of \(\pi\).
Some positive numbers that are wrapped to the point \((0, 1)\) are \(\dfrac{\pi}{2}, \dfrac{5\pi}{2}, \dfrac{9\pi}{2}\).
Some negative numbers that are wrapped to the point \((0, 1)\) are \(-\dfrac{\pi}{2}, -\dfrac{5\pi}{2}, -\dfrac{9\pi}{2}\).
Some positive numbers that are wrapped to the point \((0, -1)\) are \(\dfrac{3\pi}{2}, \dfrac{7\pi}{2}, \dfrac{11\pi}{2}\).
Some negative numbers that are wrapped to the point \((0, -1)\) are \(-\dfrac{3\pi}{2}, -\dfrac{5\pi}{2}, -\dfrac{11\pi}{2}\).
One thing we should see from our work in exercise 1.1 is that integer multiples of \(\pi\) are wrapped either to the point \((1, 0)\) or \((-1, 0)\) and that odd integer multiples of \(\dfrac{\pi}{2}\) are wrapped to either to the point \((0, 1)\) or \((0, -1)\). Since the circumference of the unit circle is \(2\pi\), it is not surprising that fractional parts of \(\pi\) and the integer multiples of these fractional parts of \(\pi\) can be located on the unit circle. This will be studied in the next exercise.
Exercise \(\PageIndex{2}\)
The following diagram is a unit circle with \(24\) points equally space points plotted on the circle. Since the circumference of the circle is \(2\pi\) units, the increment between two consecutive points on the circle is \(\dfrac{2\pi}{24} = \dfrac{\pi}{12}\).
Label each point with the smallest nonnegative real number \(t\) to which it corresponds. For example, the point \((1, 0)\) on the x-axis corresponds to \(t = 0\). Moving
counterclockwise from this point, the second point corresponds to \(\dfrac{2\pi}{12} = \dfrac{\pi}{6}\).
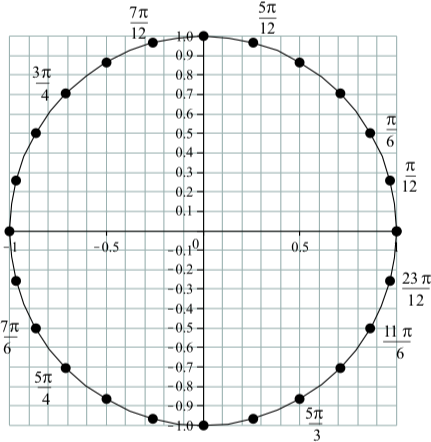
Figure \(\PageIndex{4}\): Points on the unit circle
Using \(\PageIndex{4}\), approximate the \(x\)-coordinate and the \(y\)-coordinate of each of the following:
- The point on the unit circle that corresponds to \(t =\dfrac{\pi}{3}\).
- The point on the unit circle that corresponds to \(t =\dfrac{2\pi}{3}\).
- The point on the unit circle that corresponds to \(t =\dfrac{4\pi}{3}\).
- The point on the unit circle that corresponds to \(t =\dfrac{5\pi}{3}\).
- The point on the unit circle that corresponds to \(t = \dfrac{\pi}{4}\).
- The point on the unit circle that corresponds to \(t =\dfrac{7\pi}{4}\).
- Answer
-
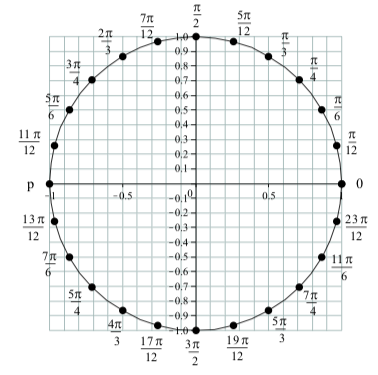
For \(t = \dfrac{\pi}{3}\), the point is approximately \((0.5, 0.87)\). For \(t = \dfrac{2\pi}{3}\), the point is approximately \((-0.5, 0.87)\). For \(t = \dfrac{4\pi}{3}\), the point is approximately \((-0.5, -0.87)\). For \(t = \dfrac{5\pi}{3}\), the point is approximately \((0.5, -0.87)\). For \(t = \dfrac{\pi}{4}\), the point is approximately \((0.71, 0.71)\). For \(t = \dfrac{7\pi}{4}\), the point is approximately \((0.71, -0.71)\).
Arcs on the Unit Circle
When we wrap the number line around the unit circle, any closed interval on the number line gets mapped to a continuous piece of the unit circle. These pieces are called arcs of the circle. For example, the segment \(\Big[0, \dfrac{\pi}{2}\Big]\) on the number line gets mapped to the arc connecting the points \((1, 0)\) and \((0, 1)\) on the unit circle as shown in \(\PageIndex{5}\). In general, when a closed interval \([a, b]\)is mapped to an arc on the unit circle, the point corresponding to \(t = a\) is called the initial point of the arc, and the point corresponding to \(t = a\) is called the terminal point of the arc. So the arc corresponding to the closed interval \(\Big(0, \dfrac{\pi}{2}\Big)\) has initial point \((1, 0)\) and terminal point \((0, 1)\).
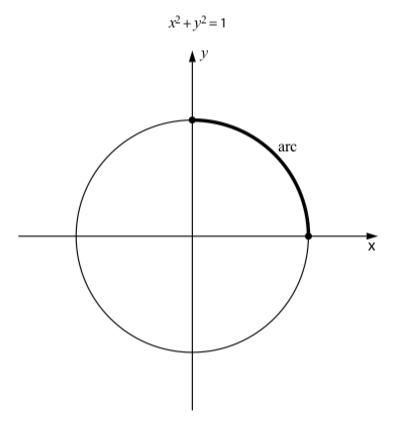
Figure \(\PageIndex{5}\): An arc on the unit circle
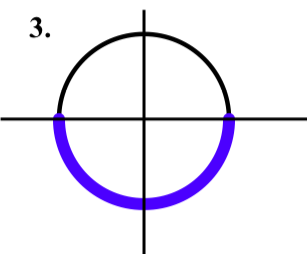
Exercise \(\PageIndex{3}\)
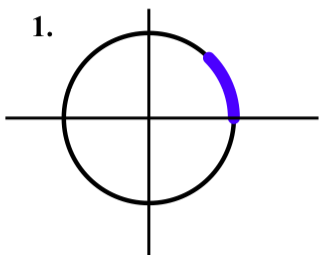
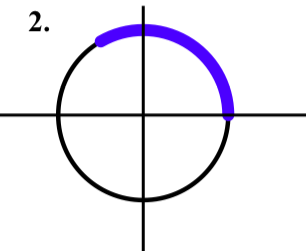
Draw the following arcs on the unit circle.
- The arc that is determined by the interval \([0, \dfrac{\pi}{4}]\) on the number line.
- The arc that is determined by the interval \([0, \dfrac{2\pi}{3}]\) on the number line.
- The arc that is determined by the interval \([0, -\pi]\) on the number line.
- Answer
-
Coordinates of Points on the Unit Circle
When we have an equation (usually in terms of \(x\) and \(y\)) for a curve in the plane and we know one of the coordinates of a point on that curve, we can use the equation to determine the other coordinate for the point on the curve. The equation for the unit circle is \(x^2+y^2 = 1\). So if we know one of the two coordinates of a point on the unit circle, we can substitute that value into the equation and solve for the value(s) of the other variable.
For example, suppose we know that the x-coordinate of a point on the unit circle is \(-\dfrac{1}{3}\). This is illustrated on the following diagram. This diagram shows the unit circle \(x^2+y^2 = 1\) and the vertical line \(x = -\dfrac{1}{3}\). This shows that there are two points on the unit circle whose x-coordinate is \(-\dfrac{1}{3}\). We can find the \(y\)-coordinates by substituting the \(x\)-value into the equation and solving for \(y\).
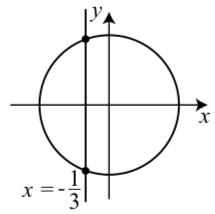
\[\begin{align*} x^2+y^2 &= 1 \\[4pt] (-\dfrac{1}{3})^2+y^2 &= 1 \\[4pt] \dfrac{1}{9}+y^2 &= 1 \\[4pt] y^2 &= \dfrac{8}{9} \end{align*}\]
Since \(y^2 = \dfrac{8}{9}\), we see that \(y = \pm\sqrt{\dfrac{8}{9}}\) and so \(y = \pm\dfrac{\sqrt{8}}{3}\). So the two points on the unit circle whose \(x\)-coordinate is \(-\dfrac{1}{3}\) are
\[ \left(-\dfrac{1}{3}, \dfrac{\sqrt{8}}{3}\right),\]
which is in the second quadrant and
\[ \left(-\dfrac{1}{3}, -\dfrac{\sqrt{8}}{3}\right),\]
which is in the third quadrant.
The first point is in the second quadrant and the second point is in the third quadrant. We can now use a calculator to verify that \(\dfrac{\sqrt{8}}{3} \approx 0.9428\). This seems consistent with the diagram we used for this problem.
Exercise \(\PageIndex{4}\)
- Find all points on the unit circle whose \(y\)-coordinate is \(\dfrac{1}{2}\).
- Find all points on the unit circle whose x-coordinate is \(\dfrac{\sqrt{5}}{4}\).
- Answer
-
- We substitute \(y = \dfrac{1}{2}\) into \(x^{2} + y^{2} = 1\).
\[x^{2} + (\dfrac{1}{2})^{2} = 1\]
\[x^{2} = \dfrac{3}{4}\]
\[x = \pm\dfrac{\sqrt{3}}{2}\]The two points are \((\dfrac{\sqrt{3}}{2}, \dfrac{1}{2})\) and \((-\dfrac{\sqrt{3}}{2}, \dfrac{1}{2})\)
-
- We substitute \(y = \dfrac{\sqrt{5}}{4}\) into \(x^{2} + y^{2} = 1\).
-
\[(\dfrac{\sqrt{5}}{4})^{2} + y^{2} = 1\]
\[y^{2} = \dfrac{11}{16}\]
\[x = \pm\dfrac{\sqrt{11}}{4}\]The two points are \((\dfrac{\sqrt{5}}{4}, \dfrac{\sqrt{11}}{4})\) and \((\dfrac{\sqrt{5}}{4}, -\dfrac{\sqrt{11}}{4})\).
Summary
In this section, we studied the following important concepts and ideas:
- The unit circle is the circle of radius 1 that is centered at the origin. The equation of the unit circle is \(x^2+y^2 = 1\). It is important because we will use this as a tool to model periodic phenomena.
- We “wrap” the number line about the unit circle by drawing a number line that is tangent to the unit circle at the point \((1, 0)\). We wrap the positive part of the number line around the unit circle in the counterclockwise direction and wrap the negative part of the number line around the unit circle in the clockwise direction.
- When we wrap the number line around the unit circle, any closed interval of real numbers gets mapped to a continuous piece of the unit circle, which is called an arc of the circle. When the closed interval \((a, b)\)is mapped to an arc on the unit circle, the point corresponding to \(t = a\) is called the initial point of the arc, and the point corresponding to \(t = a\) is called the terminal point of the arc.


