1.4: Velocity and Angular Velocity
- Page ID
- 7100
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- What is arc length?
- What is the difference between linear velocity and angular velocity?
- What are the formulas that relate linear velocity to angular velocity?
Beginning Activity
- What is the formula for the circumference \(C\) of a circle whose radius is \(r\)?
- Suppose person \(A\) walks along the circumference of a circle with a radius of 10 feet, and person B walks along the circumference of a circle of radius 20 feet. Also, suppose it takes both \(A\) and \(B\) 1 minute to walk one-quarter of the circumference of their respective circles (one-quarter of a complete revolution). Who walked the most distance?
- Suppose both people continue walking at the same pace they did for the first minute. How many complete revolutions of the circle will each person walk in 8 minutes? In 10 minutes?
Arc Length on a Circle
In Section 1.3, we learned that the radian measure of an angle was equal to the length of the arc on the unit circle associated with that angle. So an arc of length 1 on the unit circle subtends an angle of 1 radian. There will be times when it will also be useful to know the length of arcs on other circles that subtend the same angle.
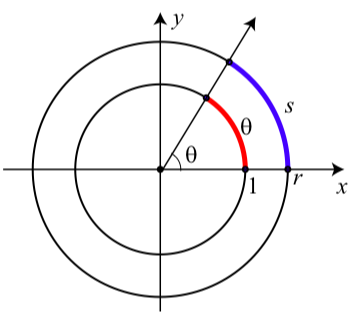
Figure \(\PageIndex{1}\): Arcs subtended by an angle of 1 radian.
In Figure \(\PageIndex{1}\), the inner circle has a radius of 1, the outer circle has a radius of \(r\), and the angle shown has a measure of \(\theta\) radians. So the arc length on the unit circle subtended by the angle is \(\theta\), and we have used s to represent the arc length on the circle of radius \(r\) subtended by the angle.
Recall that the circumference of a circle of radius \(r\) is \(2\pi r\) while the circumference of the circle of radius 1 is \(2\pi\). Therefore, the ratio of an arc length \(s\) on the circle of radius \(r\) that subtends an angle of \(\theta\) radians to the corresponding arc on the unit circle is \(\dfrac{2\pi r}{2\pi} = r\). So it follows that
\[\dfrac{s}{\theta} = \dfrac{2\pi r}{\pi}\]
\[s = r\theta\]
Definition
On a circle of radius \(r\), the arc length s intercepted by a central angle with radian measure is
\[s = r\theta\]
Note
It is important to remember that to calculate arc length , we must measure the central angle in radians.
(It is not clear why the letter \(s\) is usually used to represent arc length. One explanation is that the arc “subtends” an angle.)
Exercise \(\PageIndex{1}\)
Using the circles in the beginning activity for this section:
- Use the formula for arc length to determine the arc length on a circle of radius 10 feet that subtends a central angle of \(\dfrac{\pi}{2}\) radians. Is the result equal to one-quarter of the circumference of the circle?
- Use the formula for arc length to determine the arc length on a circle of radius 20 feet that subtends a central angle of \(\dfrac{\pi}{2}\) radians. Is the result equal to one-quarter of the circumference of the circle?
- Determine the arc length on a circle of radius 3 feet that is subtended by an angle of \(22^\circ\).
- Answer
-
- Use the formula \(s = r\theta\). \[s = r\theta = (10ft)\dfrac{\pi}{2}\] \[s = 5\pi\] The arc length is \(5\pi\) feet.
- Use the formula \(s = r\theta\). \[s = r\theta = (20ft)\dfrac{\pi}{2}\] \[s = 5\pi\] The arc length is \(10\pi\) feet.
- First convert \(22^\circ\) to radians. So \(\theta = 22^\circ \times (\dfrac{\pi rad}{180^\circ}) = \dfrac{11\pi}{90}\), and \[s = r\theta = (3ft)\dfrac{11\pi}{90}\] \[s = \dfrac{11\pi}{30}\] The arc length is \(\dfrac{11\pi}{30}\) feet or about \(1.1519\) feet.
Why Radians?
Degree measure is familiar and convenient, so why do we introduce the unit of radian? This is a good question, but one with a subtle answer. As we just saw, the length \(s\) of an arc on a circle of radius \(r\) subtended by angle of \(\theta\) radians is given by \(s = r\theta\), so \(\theta = \dfrac{s}{r}\). As a result, a radian is a ratio of two lengths (the quotient of the length of an arc by a radius of a circle), which makes a radian a dimensionless quantity. Thus, a measurement in radians can just be thought of as a real number. This is convenient for dealing with arc length (and angular velocity as we will soon see), and it will also be useful when we study periodic phenomena in Chapter 2. For this reason radian measure is universally used in mathematics, physics, and engineering as opposed to degrees, because when we use degree measure we al- ways have to take the degree dimension into account in computations. This means that radian measure is actually more natural from a mathematical standpoint than degree measure.
Linear and Angular Velocity
The connection between an arc on a circle and the angle it subtends measured in radians allows us to define quantities related to motion on a circle. Objects traveling along circular paths exhibit two types of velocity: linear and angular velocity. Think of spinning on a merry-go-round. If you drop a pebble off the edge of a moving merry-go-round, the pebble will not drop straight down. Instead, it will continue to move forward with the velocity the merry-go-round had the moment the pebble was released. This is the linear velocity of the pebble. The linear velocity measures how the arc length changes over time.
Consider a point \(P\) moving at a constant velocity along the circumference of a circle of radius \(r\). This is called uniform circular motion. Suppose that P moves a distance of s units in time \(t\). The linear velocity v of the point \(P\) is the distance it traveled divided by the time elapsed. That is, \(v = \dfrac{s}{t}\). The distance s is the arc length and we know that \(s = r\theta\).
Definition: linear velocity
Consider a point \(P\) moving at a constant velocity along the circumference of a circle of radius \(r\). The linear velocity \(v\) of the point \(P\) is given by
\[v = \dfrac{s}{t} = \dfrac{r\theta}{t}\]
where \(\theta\), measured in radians, is the central angle subtended by the arc of length \(s\).
Another way to measure how fast an object is moving at a constant speed on a circular path is called angular velocity. Whereas the linear velocity measures how the arc length changes over time, the angular velocity is a measure of how fast the central angle is changing over time.
Definition: angular velocity
Consider a point P moving with constant velocity along the circumference of a circle of radius r on an arc that corresponds to a central angle of measure \(\theta\) (in radians). The angular velocity \(\omega\) of the point is the radian measure of the angle \(\theta\) divided by the time t it takes to sweep out this angle. That is
\[\omega = \dfrac{\theta}{t}.\]
Note
The symbol \(\omega\) is the lower case Greek letter “omega.” Also, notice that the angular velocity does not depend on the radius r.
This is a somewhat specialized definition of angular velocity that is slightly different than a common term used to describe how fast a point is revolving around a circle. This term is revolutions per minute or rpm. Sometimes the unit revolutions per second is used. A better way to represent revolutions per minute is to use the “unit fraction” \(\dfrac{rev}{min}\). Since 1 revolution is \(2\pi\) radians, we see that if an object min is moving at x revolutions per minute, then
\[\omega = x \dfrac{rev}{min} \cdot \dfrac{2\pi rad}{rev} = x(2\pi)\dfrac{rad}{min}.\]
Exercise \(\PageIndex{2}\)
Suppose a circular disk is rotating at a rate of 40 revolutions per minute. We wish to determine the linear velocity v (in feet per second) of a point that is 3 feet from the center of the disk.
- Determine the angular velocity \(\omega\) of the point in radians per minute. Hint: Use the formula \[\omega = x \dfrac{rev}{min} \cdot \dfrac{2\pi rad}{rev}.\]
- We now know \(\omega = \dfrac{\theta}{t}\). So use the formula \(v = \dfrac{r\theta}{t}\) to determine \(v\) in feet per minute.
- Finally, convert the linear velocity v in feet per minute to feet per second.
- Answer
-
1. We see that
\[\omega = 40\dfrac{rev}{min} \times \dfrac{2\pi\space rad}{rev}\]
\[\omega = 80\pi\dfrac{rad}{min}\]2. The result from part (a) gives
\[v = r(\dfrac{\theta}{r}) = r\omega\]
\[v = (3ft) \times 80\pi\dfrac{rad}{min}\]
\[v = 240\pi\dfrac{ft}{min}\]3. We now convert feet per minute to feet per second.
\[v = 240\pi\dfrac{ft}{min} \times \dfrac{1\space min}{60\space sec}\]
\[v = 4\pi\dfrac{ft}{sec} \approx 12.566\dfrac{ft}{sec}\]
Notice that in Exercise 1.18, once we determined the angular velocity, we were able to determine the linear velocity. What we did in this specific case we can do in general. There is a simple formula that directly relates linear velocity to angular velocity. Our formula for linear velocity is \(v =\dfrac{s}{t} \dfrac{r\theta}{t}\). Notice that we can write this is \(v = r\dfrac{\theta}{t}\). That is, \(v = r\omega\)
Note
Consider a point \(P\) moving with constant (linear) velocity \(v\) along the circumference of a circle of radius \(r\). If the angular velocity is \(\omega\), then
\[v = r\omega\]
So in Exercise 1.18, once we determined that \(\omega = 80\pi \dfrac{rad}{min}\), we could determine v as follows:
\[v = r\omega = (3\space ft)(80\pi\dfrac{rad}{min} = 240\pi\dfrac{ft}{min}).\]
Notice that since radians are “unit-less”, we can drop them when dealing with equations such as the preceding one.
Example \(\PageIndex{1}\): Linear and Angular Velocity
The LP (long play) or 331 rpm vinyl record is an analog sound storage medium and has been used for a long time to listen to music. An LP is usually 12 inches or 10 inches in diameter. In order to work with our formulas for linear and angular velocity, we need to know the angular velocity in radians per time unit. To do this, we will convert \(33\dfrac{1}{3}\) revolutions per minute to radians per minute. We will use the fact that \(33\dfrac{1}{3} = \dfrac{100}{3}\)
\[\omega = \dfrac{100}{3}\dfrac{rev}{min} \times \dfrac{2\pi \space rad}{1\space rev} = \dfrac{200\pi}{3}\dfrac{rad}{min}\]
We can now use the formula v D r! to determine the linear velocity of a point on the edge of a 12 inch LP. The radius is 6 inches and so
\[v = r\omega = (6\space inches)(\dfrac{200\pi}{3}\dfrac{rad}{min}) = 400\pi \dfrac{inches}{min}\]
It might be more convenient to express this as a decimal value in inches per second. So we get
\[v = 400\pi \dfrac{inches}{min} \times \dfrac{1\space min}{60 \space sec} \approx 20. 944\dfrac{inches}{sec}\]
The linear velocity is approximately 20.944 inches per second.
Exercise \(\PageIndex{3}\)
For these problems, we will assume that the Earth is a sphere with a radius of 3959 miles. As the Earth rotates on its axis, a person standing on the Earth will travel in a circle that is perpendicular to the axis.
- The Earth rotates on its axis once every \(24\) hours. Determine the angular velocity of the Earth in radians per hour. (Leave your answer in terms of the number ��\(\pi\).)
- As the Earth rotates, a person standing on the equator will travel in a circle whose radius is 3959 miles. Determine the linear velocity of this person in miles per hour.
- As the Earth rotates, a person standing at a point whose latitude is \(60^\circ\) north will travel in a circle of radius 2800 miles. Determine the linear velocity of this person in miles per hour and feet per second.
- Answer
-
- One revolution corresponds to \(2\pi\) radians. So \[\omega = \dfrac{2\pi\space rad}{24\space hr} = \dfrac{\pi\space rad}{12\space hr}.\]
- To determine the linear velocity, we use the formula \(v = r\omega\) \[v = r\omega = (3959mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{3959\pi}{12}\dfrac{mi}{hr}\] The linear velocity is approximately 1036.5 miles per hour.
- To determine the linear velocity, we use the formula \(v = r\omega\) \[v = r\omega = (2800mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{2800\pi}{12}\dfrac{mi}{hr}\] The linear velocity is approximately 733.04 miles per hour. To convert this to feet per second, we use the facts that there are 5280 feet in one mile, 60 minutes in an hour, and 60 seconds in a minute. So
\[v = (\dfrac{2800\pi}{12}\dfrac{mi}{hr})(\dfrac{5280\space ft}{1\space mi})(\dfrac{1\space hr}{60\space min})(\dfrac{1\space min}{60\space sec}) = \dfrac{(2800\pi)(5280)}{12\cdot 60\cdot 60}\dfrac{ft}{sec}\]
So the linear velocity is approximately \(1075.1\) feet per second.
Summary
In this section, we studied the following important concepts and ideas:
- On a circle of radius \(r\), the arc length \(s\) intercepted by a central angle with radian measure is \[s = r\theta\]
- Uniform circular motion is when a point moves at a constant velocity along the circumference of a circle. The linear velocity is the arc length traveled by the point divided by the time elapsed. Whereas the linear velocity measures how the arc length changes over time, the angular velocity is a measure of how fast the central angle is changing over time. The angular velocity of the point is the radian measure of the angle divided by the time it takes to sweep out this angle.
- For a point \(P\) moving with constant (linear) velocity v along the circumference of a circle of radius \(r\), we have \[v = r\omega\]where \(\omega\) is the angular velocity of the point.


