1.5: Common Arcs and Reference Arcs
- Page ID
- 7101
Focus Questions
After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- How do we determine the values for cosine and sine for arcs whose endpoints are on the \(x\)-axis or the \(y\)-axis?
- What are the exact values of cosine and sine for \(t = \dfrac{\pi}{6}, t = \dfrac{\pi}{4}\) and \(t = \dfrac{\pi}{3}\)?
- What is the reference arc for a given arc? How do we determine the reference arc for a given arc?
- How do we use reference arcs to calculate the values of the cosine and sine at other arcs that have \(\dfrac{\pi}{6}, \dfrac{\pi}{4}\) or \(t = \dfrac{\pi}{3}\) as reference arcs?
Beginning Activity
Figure \(\PageIndex{1}\) shows a unit circle with the terminal points for some arcs between 0 and \(2\pi\). In addition, there are four line segments drawn on the diagram that form a rectangle. The line segments go from: (1) the terminal point for \(t = \dfrac{\pi}{6}\) to the terminal point for \(t = \dfrac{5\pi}{6}\);
(2) the terminal point for \(t = \dfrac{5\pi}{6}\) to the terminal point for \(t = \dfrac{7\pi}{6}\);
(3)the terminal point for \(t = \dfrac{7\pi}{6}\) to the terminal point for \(t = \dfrac{11\pi}{6}\);
and (4) the terminal point for \(t = \dfrac{11\pi}{6}\) to the terminal point for \(t = \dfrac{\pi}{6}\);
- What are the approximate values of \(\cos(\dfrac{\pi}{6})\) and \(\sin(\dfrac{\pi}{6})\)?
- What are the approximate values of \(\cos(\dfrac{5\pi}{6})\) and \(\sin(\dfrac{5\pi}{6})\)?
- What are the approximate values of \(\cos(\dfrac{7\pi}{6})\) and \(\sin(\dfrac{7\pi}{6})\)?
- What are the approximate values of \(\cos(\dfrac{11\pi}{6})\) and \(\sin(\dfrac{11\pi}{6})\)?
- Draw a similar rectangle on Figure 1.17 connecting the terminal points for \(t = \dfrac{\pi}{4}\), \(t = \dfrac{3\pi}{4}\), \(t = \dfrac{5\pi}{4}\), and \(t = \dfrac{7\pi}{4}\). How do the cosine and sine values for these arcs appear to be related?
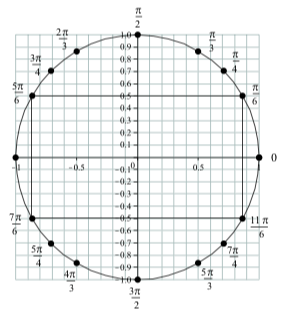
Figure \(\PageIndex{1}\): Some Arcs on the unit circle
Our task in this section is to determine the exact cosine and sine values for all of the arcs whose terminal points are shown in Figure \(\PageIndex{1}\). We first notice that we already know the cosine and sine values for the arcs whose terminal points are on one of the coordinate axes. These values are shown in the following table.
| \(t\) | 0 | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) | \(2\pi\) |
|---|---|---|---|---|---|
| \(\cos(t)\) | 1 | 0 | -1 | 0 | 1 |
| \(\sin(t)\) | 0 | 1 | 0 | -1 | 0 |
The purpose of the beginning activity was to show that we determine the values of cosine and sine for the other arcs by finding only the cosine and sine values for the arcs whose terminal points are in the first quadrant. So this is our first task. To do this, we will rely on some facts about certain right triangles. The three triangles we will use are shown in Figure 1.18.
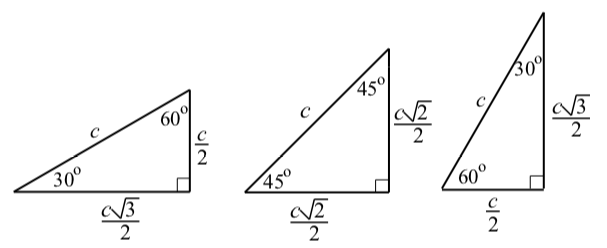
Figure \(\PageIndex{2}\): Special Right Triangles.
In each figure, the hypotenuse of the right triangle has a length of c units. The lengths of the other sides are determined using the Pythagorean Theorem. An explanation of how these lengths were determined can be found on page 420 in Appendix C. The usual convention is to use degree measure for angles when we work with triangles, but we can easily convert these degree measures to radian measures.
- A 30\(^\circ\) angle has a radian measure of \(\dfrac{\pi}{6}\) radians.
- A 45\(^\circ\) angle has a radian measure of \(\dfrac{\pi}{4}\) radians.
- A 60\(^\circ\) angle has a radian measure of \(\dfrac{\pi}{3}\) radians.
The Values of Cosine and Sine at \(t = \dfrac{\pi}{6}\)
Figure \(\PageIndex{3}\) shows the unit circle in the first quadrant with an arc in standard position of length. The terminal point of the arc is the point P and its coordinates are \((\cos(\dfrac{\pi}{6}), \sin(\dfrac{\pi}{6}))\). So from the diagram, we see that
\[x = \cos(\dfrac{\pi}{6})\space and \space y = \sin(\dfrac{\pi}{6})\]
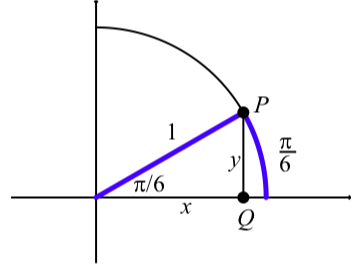
Figure \(\PageIndex{3}\): The arc and its associated angle
As shown in the diagram, we form a right triangle by drawing a line from \(P\) that is perpendicular to the \(x\)-axis and intersects the \(x\)-axis at \(Q\). So in this right triangle, the angle associated with the arc is \(\dfrac{\pi}{6}\) radians or \(30^\circ\). From what we know about this type of right triangle, the other acute angle in the right triangle is \(60^\circ\) or \(\dfrac{\pi}{3}\) radians. We can then use the results shown in the triangle on the left in Figure \(\PageIndex{2}\) to conclude that \(x = \dfrac{\sqrt{3}}{2}\) and \(y = \dfrac{1}{2}\). (Since in this case, \(c = 1\).) Therefore, we have just proved that
\[\cos(\dfrac{\pi}{6} = \dfrac{\sqrt{3}}{2}) \space and \space \sin(\dfrac{\pi}{6}) = \dfrac{1}{2}\]
Exercise \(\PageIndex{1}\)
In the beginning activity for this section, we used the unit circle to approximate the values of the cosine and sine functions at \(t = \dfrac{\pi}{6}\), \(t = \dfrac{5\pi}{6}\), \(t = \dfrac{7\pi}{6}\), and \(t = \dfrac{11\pi}{6}\). We also saw that these values are all related and that once we have values for the cosine and sine functions at \(t = \dfrac{\pi}{6}\), we can use our knowledge of the four quadrants to determine these function values at \(t = \dfrac{5\pi}{6}\), \(t = \dfrac{7\pi}{6}\), and \(t = \dfrac{11\pi}{6}\). Now that we know that \[\cos(\dfrac{\pi}{6}) = \dfrac{\sqrt{\pi}}{6} = \dfrac{1}{2},\]
determine the exact values of each of the following:
- \(\cos(\dfrac{5\pi}{6})\) and \(\sin(\dfrac{5\pi}{6})\)
- \(\cos(\dfrac{7\pi}{6})\) and \(\sin(\dfrac{7\pi}{6})\)
- \(\cos(\dfrac{11\pi}{6})\) and \(\sin(\dfrac{11\pi}{6})\)
- Answer
-
- \(\cos(\dfrac{5\pi}{6}) = -\dfrac{\sqrt{3}}{2}\) and \(\sin(\dfrac{5\pi}{6}) = \dfrac{1}{2}\)
- \(\cos(\dfrac{7\pi}{6}) = -\dfrac{\sqrt{3}}{2}\) and \(\sin(\dfrac{7\pi}{6}) = -\dfrac{1}{2}\)
- \(\cos(\dfrac{11\pi}{6}) = -\dfrac{\sqrt{3}}{2}\) and \(\sin(\dfrac{11\pi}{6}) = -\dfrac{1}{2}\)
The Values of Cosine and Sine at \(t = \dfrac{\pi}{4}\)
Figure \(\PageIndex{4}\) shows the unit circle in the first quadrant with an arc in standard position of length \(\dfrac{\pi}{4}\). The terminal point of the arc is the point \(P\) and its coordinates are \((\cos(\dfrac{\pi}{4}), \sin(\dfrac{\pi}{4}))\). So from the diagram, we see that
\[x = \cos(\dfrac{\pi}{4})\space and \space y = \sin(\dfrac{\pi}{4})\]
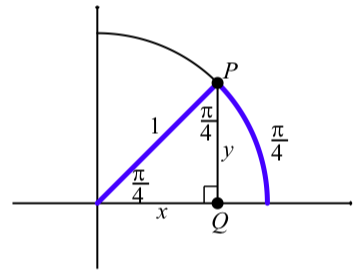
Figure \(\PageIndex{4}\): The arc \(\dfrac{\pi}{4}\) and its associated angle.
As shown in the diagram, we form a right triangle by drawing a line from \(P\) that is perpendicular to the x-axis and intersects the x-axis at \(Q\). So in this right triangle, the acute angles are \(\dfrac{\pi}{4}\) radians or \(45^\circ\). We can then use the results shown in the triangle in the middle of Figure \(\PageIndex{2}\) to conclude that \(x = \dfrac{\sqrt{2}}{2}\) and \(y = \dfrac{\sqrt{2}}{2}\). (Since in this case, \(c = 1\).) Therefore, we have just proved that \[cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2} \space and \space sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}.\]
Exercise \(\PageIndex{2}\)
Now that we know that \[cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2} \space and \space sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}.\]
use a method similar to the one used in Exercise 1.21 to determine the exact values of each of the following:
- \(\cos(\dfrac{3\pi}{4}) \space and \space \sin(\dfrac{3\pi}{4}).\)
- \(\cos(\dfrac{5\pi}{4}) \space and \space \sin(\dfrac{5\pi}{4}).\)
- \(\cos(\dfrac{7\pi}{4}) \space and \space \sin(\dfrac{7\pi}{4}).\)
- Answer
-
- \(\cos(\dfrac{3\pi}{4}) = -\dfrac{\sqrt{2}}{2}\) and \(\sin(\dfrac{3\pi}{4}) = \dfrac{\sqrt{2}}{2}\)
- \(\cos(\dfrac{7\pi}{6}) = -\dfrac{\sqrt{2}}{2}\) and \(\sin(\dfrac{7\pi}{6}) = -\dfrac{\sqrt{2}}{2}\)
- \(\cos(\dfrac{11\pi}{6}) = \dfrac{\sqrt{2}}{2}\) and \(\sin(\dfrac{11\pi}{6}) = -\dfrac{\sqrt{2}}{2}\)
The Values of Cosine and Sine at \(t = \dfrac{\pi}{3}\)
Figure \(\PageIndex{4}\) shows the unit circle in the first quadrant with an arc in standard position of length \(\dfrac{\pi}{3}\). The terminal point of the arc is the point P and its coordinates are \((\cos(\dfrac{\pi}{3}), \sin(\dfrac{\pi}{3}))\). So from the diagram, we see that \[x = \cos(\dfrac{\pi}{3})\space and \space y = \sin(\dfrac{\pi}{3})\]
As shown in the diagram, we form a right triangle by drawing a line from \(P\) that is perpendicular to the x-axis and intersects the \(x\)-axis at \(Q\). So in this right triangle, the angle associated with the arc is \(\dfrac{\pi}{3}\) radians or \(60^\circ\). From what we know about this type of right triangle, the other acute angle in the right triangle is \(30^\circ\)
or \(\dfrac{\pi}{6}\) radians. We can then use the results shown in the triangle on the right in Figure \(\PageIndex{5}\) to conclude that \(x= \dfrac{1}{2} \space and \space y = \dfrac{\sqrt{3}}{2}.\). (Since in this case, \(c = 1\).)
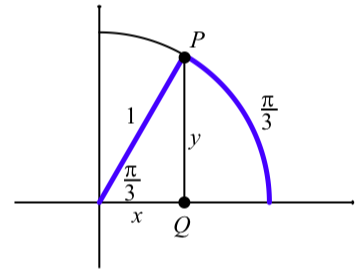
Figure \(\PageIndex{5}\): The arc \(\dfrac{\pi}{3}\) and its associated angle.
Therefore, we have just proved that \[\cos(\dfrac{\pi}{3}) = \dfrac{1}{2} \space and \space \sin(\dfrac{\pi}{3}) = \dfrac{\sqrt{3}}{2}.\]
Reference Arcs (Reference Angles)
In the beginning activity for this section and in Exercises 1.21 and 1.22, we saw that we could relate the coordinates of the terminal point of an arc of length greater than \(\dfrac{\pi}{2}\) on the unit circle to the coordinates of the terminal point of an arc of length between \(0\) and \(\dfrac{\pi}{2}\) on the unit circle. This was intended to show that we can do this for any angle of length greater than \(\dfrac{\pi}{2}\), and this means that if we know the values of the cosine and sine for any arc (or angle) between \(0\) and \(\dfrac{\pi}{2}\), then we can find the values of the cosine and sine for any arc at all. The arc between \(0\) and \(\dfrac{\pi}{2}\) to which we relate a given arc of length greater than \(\dfrac{\pi}{2}\) is called a reference arc.
Definition
The reference arc \(\hat{t}\) for an arc \(t\) is the smallest non-negative arc (always considered non-negative) between the terminal point of the arct and the closer of the two x-intercepts of the unit circle. Note that the two x-intercepts of the unit circle are \((-1, 0)\) and \((1, 0)\).
The concept of reference arc is illustrated in Figure \(\PageIndex{6}\). Each of the thicker arcs has length \(\hat{t}\) and it can be seen that the coordinates of the points in the second, third, and fourth quadrants are all related to the coordinates of the point in the first quadrant. The signs of the coordinates are all determined by the quadrant in which the point lies.
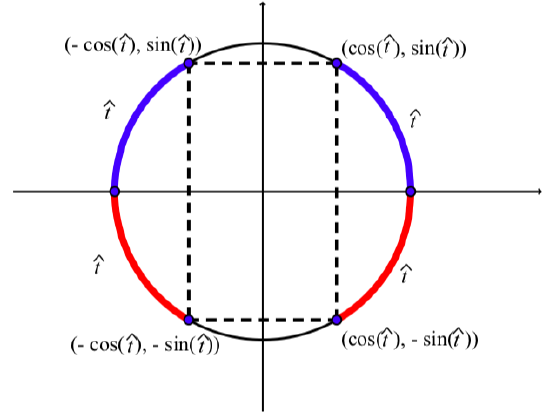
Figure \(\PageIndex{6}\): Reference arcs.
How we calculate a reference arc for a given arc of length \(t\) depends upon the quadrant in which the terminal point of \(t\) lies. The diagrams in Figure \(\PageIndex{6}\) illustrate how to calculate the reference arc for an arc of length t with \(0 \leq t \leq 2\pi\).
In Figure \(\PageIndex{6}\), we see that for an arc of length \(t\) with \(0 \leq t \leq 2\pi\):
- If \(\dfrac{\pi}{2} < t < \pi\), then the point intersecting the unit circle and the x axis that is closest to the terminal point of t is \((-1, 0)\). So the reference arc is \(\pi - t\). In this case, Figure \(\PageIndex{6}\) shows that \[\cos(\pi -t) = -\cos(t) \space and \space \sin(\pi -t) = \sin(t)\]
- If \(\pi < t < \dfrac{\pi}{2}\), then the point intersecting the unit circle and the x axis that is closest to the terminal point of t is \((-1, 0)\). So the reference arc is \(t - \pi\). In this case, Figure \(\PageIndex{6}\) shows that \[\cos(t - \pi) = -\cos(t) \space and \space \sin(t - \pi) = -\sin(t)\]
- If \(\dfrac{3\pi}{2} < t < 2\pi\), then the point intersecting the unit circle and the x axis that is closest to the terminal point of t is \((1, 0)\). So the reference arc is \(2\pi - t\). In this case, Figure \(\PageIndex{6}\) shows that \[\cos(2\pi -t) = \cos(t) \space and \space \sin(2\pi -t) = -\sin(t)\]
Exercise \(\PageIndex{3}\)
For each of the following arcs, draw a picture of the arc on the unit circle. Then determine the reference arc for that arc and draw the reference arc in the first quadrant.
- \(t = \dfrac{5\pi}{4}\)
- \(t = \dfrac{4\pi}{5}\)
- \(t = \dfrac{5\pi}{3}\)
- Answer
-
As shown in the following diagram:
The reference arc is \(\dfrac{5\pi}{4} - \pi = \dfrac{\pi}{4}\). The reference arc is \(\pi - \dfrac{4\pi}{5} = \dfrac{\pi}{5}\). The reference arc is \(2\pi - \dfrac{5\pi}{3} = \dfrac{\pi}{3}\).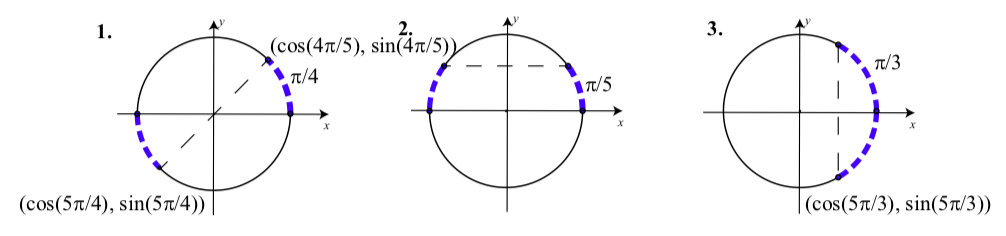
Exercise \(\PageIndex{4}\)
Although we did not use the term then, in Exercises 1.21 and 1.22, we used the facts that \(t = \dfrac{\pi}{6}\) and \(t = \dfrac{\pi}{4}\) were the reference arcs for other arcs to determine the exact values of the cosine and sine functions for those other arcs. Now use the values of \(\cos(\dfrac{\pi}{3})\) and \(\sin(\dfrac{\pi}{3})\) to determine the exact values of the cosine and sine functions for each of the following arcs:
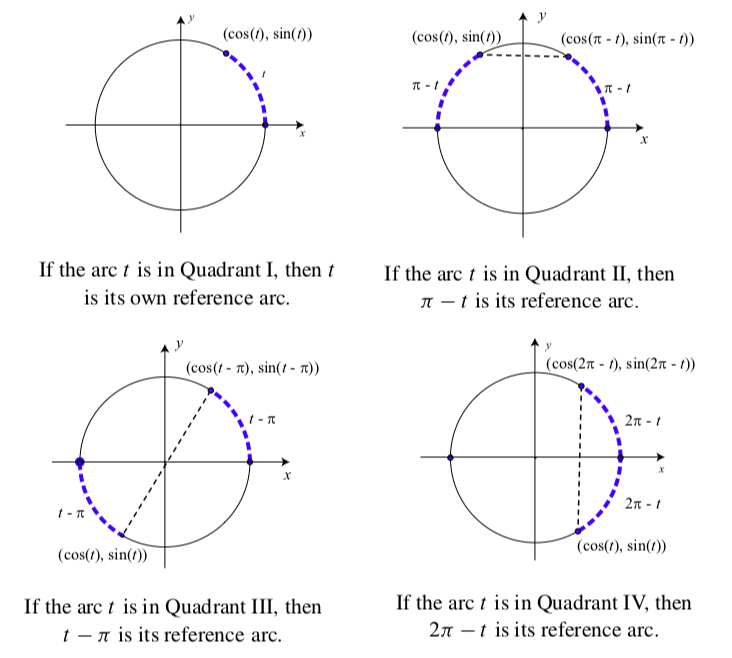
Figure \(\PageIndex{7}\): Reference arcs
- \(t = \dfrac{2\pi}{3}\)
- \(t = \dfrac{4\pi}{3}\)
- \(t = \dfrac{5\pi}{3}\)
- Answer
-
- \(\cos(\dfrac{2\pi}{3}) = -\dfrac{1}{2}\) and \(\sin(\dfrac{2\pi}{3}) = \dfrac{\sqrt{3}}{2}\)
- \(\cos(\dfrac{4\pi}{3}) = -\dfrac{1}{2}\) and \(\sin(\dfrac{4\pi}{3}) = -\dfrac{\sqrt{3}}{2}\)
- \(\cos(\dfrac{5\pi}{3}) = \dfrac{1}{2}\) and \(\sin(\dfrac{5\pi}{3}) = -\dfrac{\sqrt{3}}{2}\)
Reference Arcs for Negative Arcs
Up to now, we have only discussed reference arcs for positive arcs, but the same principles apply when we use negative arcs. Whether the arc \(t\) is positive or negative, the reference arc for t is the smallest non-negative arc formed by the terminal point of t and the nearest x-intercept of the unit circle. For example, for the arc \(t = -\dfrac{\pi}{4}\) is in the fourth quadrant, and the closer of the two x-intercepts of the unit circle is \((1, 0)\). So the reference arc is \(\hat{t} = \dfrac{\pi}{4}\) as shown in Figure 1.24.
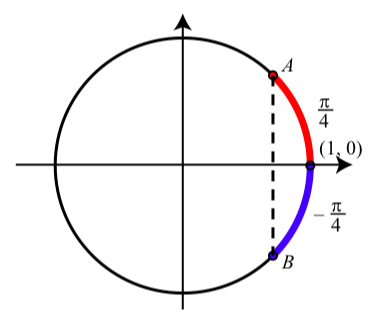
Figure \(\PageIndex{8}\): Reference Arc for \(t = \dfrac{\pi}{4}\).
Since we know that the point \(A\) has coordinates \((\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2})\), we conclude that the point \(B\) has coordinates \((\dfrac{\sqrt{2}}{2}, -\dfrac{\sqrt{2}}{2})\), and so \[\cos(-\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2} \space and \space \sin(-\dfrac{\pi}{4}) = -\dfrac{\sqrt{2}}{2}.\]
Exercise \(\PageIndex{5}\)
For each of the following arcs, determine the reference arc and the values of the cosine and sine functions.
- \(t = -\dfrac{\pi}{6}\)
- \(t = -\dfrac{2\pi}{3}\)
- \(t = -\dfrac{5\pi}{4}\)
- Answer
-
- The terminal point of \(t = -\dfrac{\pi}{6}\) is in the fourth quadrant and the reference arc for \(t = -\dfrac{\pi}{6}\) is \(\hat{t} = \dfrac{\pi}{6}\). So\[\cos(-\dfrac{\pi}{6}) = \dfrac{\sqrt{3}}{2}\] and \[\sin(-\dfrac{\pi}{6}) = -\dfrac{1}{2}\]
- The terminal point of \(t = -\dfrac{2\pi}{3}\) is in the fourth quadrant and the reference arc for \(t = -\dfrac{2\pi}{3}\) is \(\hat{t} = \dfrac{\pi}{3}\). So\[\cos(-\dfrac{2\pi}{3}) = -\dfrac{1}{2}\] and \[\sin(-\dfrac{2\pi}{3}) = -\dfrac{\sqrt{3}}{2}\]
- The terminal point of \(t = -\dfrac{5\pi}{4}\) is in the fourth quadrant and the reference arc for \(t = -\dfrac{5\pi}{4}\) is \(\hat{t} = \dfrac{\pi}{4}\). So\[\cos(-\dfrac{5\pi}{4}) = -\dfrac{\sqrt{2}}{2}\] and \[\sin(-\dfrac{5\pi}{4}) = -\dfrac{\sqrt{2}}{2}\]
Example \(\PageIndex{1}\): (Using Reference Arcs)
Sometimes we can use the concept of a reference arc even if we do not know the length of the arc but do know the value of the cosine or sine function. For example, suppose we know that \[0 < t < \dfrac{\pi}{2} \space and \space sin(t) = \dfrac{2}{3}.\]
Are there any conclusions we can make with this information? Following are some possibilities.
- We can use the Pythagorean identity to determine \(\cos(t)\) as follows: \[\cos^2(t) + \sin^2(t) = 1\] \[\cos^2(t) = 1 - \sin^2(t)\] \[\cos^2(t) = \dfrac{5}{9}\] Since t is in the first quadrant, we know that \(\cos(t)\) is positive, and hence \[\cos(t) = \sqrt{\dfrac{5}{9}} = \dfrac{\sqrt{5}}{3}\]
- Since \(0 < t < \dfrac{\pi}{2}\), \(t\) is in the first quadrant. Hence, \(\pi - t\) is in the second quadrant and the reference arc is \(t\). In the second quadrant we know that the sine is positive, so we can conclude that \[\sin(\pi - t) = \sin(t) = \dfrac{2}{3}.\]
Exercise \(\PageIndex{6}\)
Following is information from Example 1.26: \[0 < t < \dfrac{\pi}{2} \space and \space sin(t) = \dfrac{2}{3}.\] Use this information to determine the exact values of each of the following:
- \(\cos(\pi - t)\)
- \(\sin(\pi + t)\)
- \(\cos(\pi + t)\)
- \(\sin(2\pi - t)\)
- Answer
-
- We know that \(\pi - t\) is in the second quadrant with reference arc \(t\). So \[\cos(\pi - t) = -\cos(t) = \dfrac{\sqrt{5}}{3}\]
- The arc \(\pi + t\) is in the second quadrant with reference arc \(t\). So \[\sin(\pi + t) = -\sin(t) = -\dfrac{2}{3}\]
- The arc \(\pi + t\) is in the second quadrant with reference arc \(t\). So \[\cos(\pi + t) = -\cos(t) = -\dfrac{\sqrt{5}}{3}\]
- The arc \(2\pi - t\) is in the second quadrant with reference arc \(t\). So \[\sin(2\pi - t) = -\sin(t) = -\dfrac{2}{3}\]
Summary
In this section, we studied the following important concepts and ideas:
- The values of \(\cos(t)\) and \(\sin(t)\) for arcs whose terminal points are on one of the coordinate axes are shown in Table 1.3 below.
- Exact values for the cosine and sine functions at \(\dfrac{\pi}{6}\), \(\dfrac{\pi}{4}\), and \(\dfrac{\pi}{3}\) are known and are shown in Table 1.3 below.
- A reference arc for an arc t is the arc (always considered nonnegative) between the terminal point of the arc t and point intersecting the unit circle and the x-axis closest to it.
- If \(t\) is an arc that has an arc \(\hat{t}\) as a reference arc, then \(|\cos(t)|\) and \(|\cos(\hat{t})|\) are the same. Whether \(\cos(t) = \cos(\hat{t})\) or \(\cos(t) = - \cos(\hat{t})\) is determined by the quadrant in which the terminal side of \(t\) lies. The same is true for \(\sin(t)\)
- We can determine the exact values of the cosine and sine functions at any arc with \(\dfrac{\pi}{6}\), \(\dfrac{\pi}{4}\), or \(\dfrac{\pi}{3}\) as reference arc. These arcs between 0 and \(2\pi\) are shown in Figure \(\PageIndex{1}\). The results are summarized in Table 1.3 below.
| \(t\) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) | \(\dfrac{7\pi}{6}\) | \(\dfrac{5\pi}{4}\) | \(\dfrac{4\pi}{3}\) | \(\dfrac{3\pi}{2}\) | \(\dfrac{5\pi}{3}\) | \(\dfrac{7\pi}{4}\) | \(\dfrac{11\pi}{6}\) |
|
\(x=\cos(t)\) |
1 | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | 0 | \(-\dfrac{1}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | -1 | \(-\dfrac{\sqrt{3}}{2}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(-\dfrac{1}{2}\) | 0 | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{3}}{2}\) |
| \(y=\sin(t)\) | 0 | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | 1 | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | 0 | \(-\dfrac{1}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | \(-\dfrac{\sqrt{3}}{2}\) | -1 | \(-\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(-\dfrac{1}{2}\) |


