4.2: Trigonometric Equations
- Page ID
- 7119
Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- What is a trigonometric equation?
- What does it mean to solve a trigonometric equation?
- How is a trigonometric equation different from a trigonometric identity?
We have already learned how to solve certain types of trigonometric equations. In Section 2.6 we learned how to use inverse trigonometric functions to solve trigonometric equations.
Beginning Activity
Refer back to the method from Section 2.6 to find all solutions to the equation \(\sin(x) = 0.4\).
Trigonometric Equations
When a light ray from a point \(P\) reflects off a surface at a point \(R\) to illuminate a point \(Q\) as shown at left in Figure 4.1, the light makes two angles \(\alpha\) and \(\beta\) with a perpendicular to the surface. The angle \(\alpha\) is called the angle of incidence and the angle \(\beta\) is called the angle of reflection. The Law of Reflection states that when light is reflected off a surface, the angle of incidence equals the angle of reflection. What happens if the light travels through one medium (say air) from a point \(P\), deflects into another medium (say water) to travel to a point \(Q\)? Think about what happens if you look at an object in a glass of water. See Figure 4.1 at right. Again the light makes two angles \(\alpha\) and \(\beta\) with a perpendicular to the surface. The angle \(\alpha\) is called the angle of incidence and the angle \(\beta\) is called the angle of refraction. If light travels from air into water, the Law of Refraction says that \[\dfrac{\sin(\alpha)}{\sin(\beta)} = \dfrac{c_{a}}{c_{w}}\]
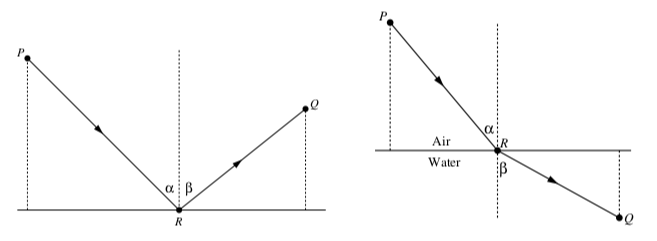
Figure \(\PageIndex{1}\): Reflection and refraction.
where \(c_{a}\) is the speed of light in air and \(c_{w}\) is the speed of light in water. The ratio \(\dfrac{c_{a}}{c_{w}}\) of the speed of light in air to the speed of light in water can be calculated by experiment. In practice, the speed of light in each medium is compared to the speed of light in a vacuum. The ratio of the speed of light in a vacuum to the speed of light in water is around 1.33. This is called the index of refraction for water. The index of refraction for air is very close to 1, so the ratio \(\dfrac{c_{a}}{c_{w}}\) is close to 1.33. We can usually measure the angle of incidence, so the Law of Refraction can tells us what the angle of refraction is by solving equation (6).
Trigonometric equations arise in a variety of situations, like in the Law of Refraction, and in a variety of disciplines including physics, chemistry, and engineering. As we develop trigonometric identities in this chapter, we will also use them to solve trigonometric equations.
Recall that Equation (6) is a conditional equation because it is not true for all allowable values of the variable. To solve a conditional equation means to find all of the values for the variables that make the two expressions on either side of the equation equal to each other.
Equations of Linear Type
Section 2.6 showed us how to solve trigonometric equations that are reducible to linear equations. We review that idea in our first example.
Example \(\PageIndex{1}\): (Solving an Equation of Linear Type)
Consider the equation \[2\sin(x) = 1.\]
We want to find all values of \(x\) that satisfy this equation. Notice that this equation looks a lot like the linear equation \(2y = 1\), with \(\sin(x)\) in place of \(y\). So this trigonometric equation is of linear type and we say that it is linear in \(\sin(x)\). We know how to solve \(2y = 1\), we simply divide both sides of the equation by 2 to obtain \(y = \dfrac{1}{2}\). We can apply the same algebraic operation to \(2\sin(x) = 1\) to obtain the equation \[\sin(x) = \dfrac{1}{2}.\]
Now we could proceed in a couple of ways. From previous work we know that \(\sin(x) = \dfrac{1}{2}\) when \(x = \dfrac{\pi}{6}\). Alternatively, we could apply the inverse sine to both sides of our equation to see that one solution is \(x = \sin^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{6}\).
Recall, however, this is not the only solution. The first task is to find all of the solutions in one complete period of the sine function. We can use the interval with \(0 \leq x \leq 2\pi\) but we often use the interval \(-\pi \leq x \leq \pi\). In this case, it makes no difference since the sine function is positive in the second quadrant. Using \(\dfrac{\pi}{6}\) as a reference angle, we see that \(x = \pi - \dfrac{\pi}{6} = \dfrac{5\pi}{6}\) is another solution of this equation. (Use a calculator to check this.)
We now use the fact that the sine function is period with a period of \(2\pi\) to write formulas that can be used to generate all solutions of the equation \(2\sin(x) = 1\).
So the angles in the first quadrant are \(\dfrac{\pi}{6} + k(2\pi)\). and the angles in the second quadrant are \(\dfrac{5\pi}{6} + k(2\pi)\) where \(k\) is an integer. So for the solutions of the equation \(2\sin(x) = 1\), we write \(x = \dfrac{\pi}{6} + k(2\pi)\) or \(x = \dfrac{5\pi}{6} + k(2\pi)\), where \(k\) is an integer.
We can always check our solutions by graphing both sides of the equation to see where the two expressions intersect. Figure 4.2 shows that graphs of \(y = 2\sin(x)\) and \(y = 1\) on the interval \([-2\pi, 3\pi]\). We can see that the points of intersection of these two curves occur at exactly the solutions we found for this equation.
Exercise \(\PageIndex{1}\)
Find the exact values of all solutions to the equation \(4\cos(x) = 2\sqrt{2}\). Do this by first finding all solutions in one complete period of the cosine function and
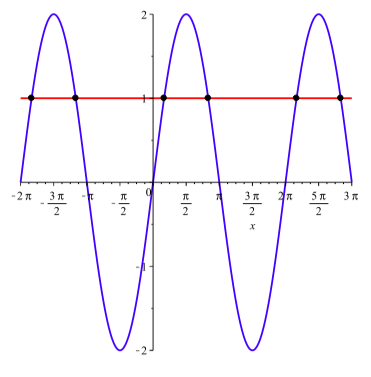
Figure \(\PageIndex{2}\): The graphs of \(y = 2\sin(x)\) and \(y = 1\)
then using the periodic property to write formulas that can be used to generate all solutions of the equation. Draw appropriate graphs to illustrate your solutions.
- Answer
-
We divide both sides of the equation \(4\cos(x) = 2\sqrt{2}\) to get \(\cos(x) = \dfrac{\sqrt{2}}{2}\). So \[x = \dfrac{\pi}{4} + k(2\pi)\] or \[x = \dfrac{7\pi}{4} + k(2\pi)\]
where \(k\) is an integer.
Solving an Equation Using an Inverse Function
When we solved the equation \(2\sin(x) = 1\), we used the fact that we know that \(\sin(\dfrac{\pi}{6}) = \dfrac{1}{2}\). When we cannot use one of the common arcs, we use the more general method of using an inverse trigonometric function. This is what we did in Section 2.6. See “A Strategy for Solving a Trigonometric Function” on page 158. We will illustrate this strategy with the equation \(\cos(x) = 0.7\). We start by applying the inverse cosine function to both sides of this equation to obtain
\[\cos(x) = 0.7\]
\[\cos^{-1}(\cos(x)) = \cos^{-1}(0.7)\]
\[x = \cos^{-1}(0.7)\]
This gives the one solution for the equation that is in interval \([0, \pi]\). Before we use the periodic property, we need to determine the other solutions for the equation in one complete period of the cosine function. We can use the interval \([0, 2\pi]\) but it is easier to use the interval \([-\pi, \pi]\). One reason for this is the following so-called “negative arc identity” stated on page 82.
\[\cos(-x) = \cos(x)\] for every real number \(x\).
Hence, since one solution for the equation is \(x = \cos^{-1}(0.7)\), another solution is \(x = -\cos^{-1}(0.7)\). This means that the two solutions of the equation \[x = \cos(x)\] on the interval \([-\pi, \pi]\) are \(x = \cos^{-1}(0.7)\) and \(x = -\cos^{-1}(0.7)\)
Since the period iof the cosine function is \(2\pi\), we can say that any solution of the equation \(\cos(x) = 0.7\) will be of the form \(x = \cos^{-1}(0.7) + k(2\pi)\) and \(x = -\cos^{-1}(0.7) + k(2\pi)\) where \(k\) is some integer.
Note
Note: The beginning activity for this section had the equation \(\sin(x) = 0.4\). The solutions for this equation are
\(x = \arcsin(0.4) + k(2\pi)\) and \(x = (\pi - \arcsin(0.4)) + k(2\pi)\) where \(k\) is some integer.
We can write the solutions in approximate form as \(x = 0.41152 + k(2\pi)\) and \(x = 2.73008 + k(2\pi)\) where \(k\) is an integer.
Exercise \(\PageIndex{2}\)
- Determine formulas that can be used to generate all solutions to the equation \(5\sin(x) = 2\). Draw appropriate graphs to illustrate your solutions in one period of the sine function.
- Approximate, to two decimal places, the angle of refraction of light passing from air to water if the angle of incidence is \(40^\circ\).
- Answer
-
1. We divide both sides of the equation \(5\sin(x) = 2\) by \(5\) to get \(\sin(x) = 0.4\).
So \[x = \sin^{-1}(0.4) + k(2\pi)\] or \[x = (\pi - \sin^{-1}(0.4)) + k(2\pi)\]
where \(k\) is an integer.
2. We use \(\alpha = 40^\circ\) and \(\dfrac{c_{a}}{c_{w}} = 1.33\) in the Law of Refraction.\[\dfrac{\sin(40^\circ)}{\sin(\beta)} = 1.33\]
\[\sin(\beta) = \dfrac{\sin(40^\circ)}{1.33} \approx 0.483299\]
\[\beta \approx 28.90^\circ\]
The angle of refraction is approximately \(28.90^\circ\).
Solving Trigonometric Equations Using Identities
We can use known trigonometric identities to help us solve certain types of trigonometric equations.
Example \(\PageIndex{1}\): (Using Identities to Solve Equations)
Consider the trigonometric equation \[\cos^{2}(x) - \sin^{2}(x) = 1\]
This equation is complicated by the fact that there are two different trigonometric functions involved. In this case we use the Pythagorean Identity \[\sin^{2}(x) + \cos^{2}(x) = 1\] by solving for \(\cos^{2}(x)\) to obtain \[\cos^{2}(x) = 1- \sin^{2}(x).\]
We can now substitute into equation (7) to get
\[(1 - \sin^{2}(x)) - \sin^{2}(x) = 1\]
Note that everything is in terms of just the sine function and we can proceed to solve the equation from here: \[(1 - \sin^{2}(x)) - \sin^{2}(x) = 1\]
\[1 - 2\sin^{2}(x) = 1\]
\[-2\sin^{2}(x) = 0\]
\[\sin^{2}(x) = 0\]
\[\sin(x) = 0\]
We know that \(\sin(x) = 0\) when \(x = \pi k\) for any integer \(k\), so the solutions to the equation \(\cos^{2}(x) - \sin^{2}(x) = 1\) are \(x = \pi k\) for any integer \(k\).
This is illustrated by Figure \(\PageIndex{3}\).
Exercise \(\PageIndex{3}\)
Find the exact values of all solutions to the equation \(\sin^{2}(x) = 3\cos^{2}(x)\). Draw appropriate graphs to illustrate your solutions.
- Answer
-
We will use the identity \(\cos^{2}(x) = 1 - \sin(x)\). So we have
\[\sin^{2}(x) = 3(1 - \sin^{2}(x))\]
\[\sin^{2}(x) = \dfrac{3}{4}\]
So we have \(\sin(x) = \dfrac{\sqrt{3}}{2}\) or \(\sin(x) = -\dfrac{\sqrt{3}}{2}\). For the first equation, we see that
\[x = \dfrac{\pi}{3} + 2\pi k\] or \[x = -\dfrac{\pi}{3} + 2\pi k\]
where \(k\) is an integer, and for the second equation, we have
\[x = \dfrac{\pi}{3} + 2\pi k\] or \[x = \dfrac{\pi}{3} + 2\pi k\]
where \(k\) is an integer. The graphs of \(y^{2} = \sin^{2}(x)\) and \(y^{2} = 3\cos^{2}(x)\) will show \(4\) points of intersection on the interval \([0, 2\pi]\).
Other Methods for Solving Trigonometric Equations
Just like we did with linear equations, we can view some trigonometric equations as quadratic in nature and use tools from algebra to solve them.
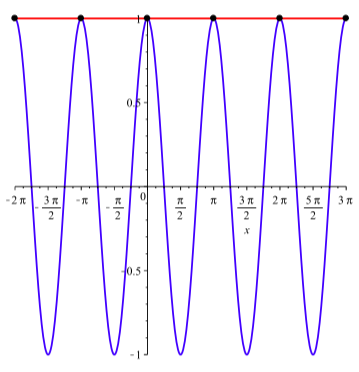
Figure \(\PageIndex{3}\): The graphs of \(y = \cos^{2}(x) - \sin^{2}(x)\) and \(y = 1\)
Example \(\PageIndex{2}\): (Solving Trigonometric Equations of Quadratic Type)
Consider the trigonometric equation \[\cos^{2}(x) - 2\cos(x) + 1 = 0\]
This equation looks like a familiar quadratic equation \(y^{2} - 2y + 1 = 0\). We can solve this quadratic equation by factoring to obtain \((y - 1)^{2} = 0\). So we can apply the same technique to the trigonometric equation \(\cos^{2}(x) - 2\cos(x) + 1 = 0\). Factoring the left hand side yields \[(\cos(x) - 1)^{2} = 0\]
The only way \((\cos(x) - 1)^{2} = 0\) can be 0 is if \((\cos(x) - 1)^{2}\) is 0. This reduces our quadratic trigonometric equation to a linear trigonometric equation. To summarize the process so far we have \[\cos^{2}(x) - 2\cos(x) + 1 = 0\]
\[(\cos(x) - 1)^{2} = 0\]
\[\cos(x) - 1 = 0\]
\[\cos(x) = 1\]
We know that \(\cos(x) = 1\) when \(x = 2\pi k\) for integer values of \(k\). Therefore, the solutions to our original equation are
\[x = 2\pi k\]
where \(k\) is any integer. As a check, the graph of \(y = \cos^{2}(x) - 2\cos(x) + 1\) is shown in Figure \(\PageIndex{4}\). The figure appears to show that the graph of \(y = \cos^{2}(x) - 2\cos(x) + 1\) intersects the \(x\)-axis at exactly the points we found, so our solution is validated by graphical means.
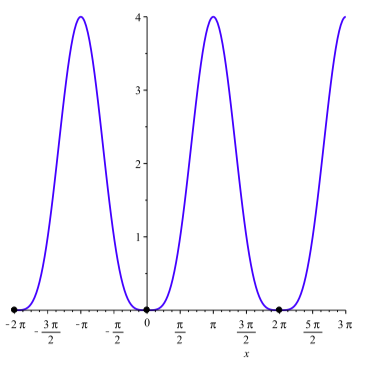
Figure \(\PageIndex{4}\): the graph of \(y = \cos^{2}(x) - 2\cos(x) + 1\)
Exercise \(\PageIndex{4}\)
Find the exact values of all solutions to the equation \(\sin^{2}(x - 4\sin(x) = -3)\). Draw appropriate graphs to illustrate your solutions.
- Answer
-
We write the equation as \(\sin(x) - 4\sin(x) + 3 = 0\) and factor the right side to get \((\sin(x) - 3)(\sin(x) - 1) = 0\). So we see that \(\sin(x) - 3 = 0\) or \(\sin(x) - 1 = 0\). However, the equation \(\sin(x) - 3 = 0\) is equivalent to \(\sin(x) = 3\), and this equation has no solution. We write \(\sin(x) - 1 = 0\) as \(\sin(x) = 1\) and so the solutions are
\[x = \dfrac{\pi}{2} + 2\pi k\]
where \(k\) is an integer.
Summary
In this section, we studied the following important concepts and ideas:
A trigonometric equation is a conditional equation that involves trigonometric functions. If it is possible to write the equation in the form
\(\text{“some trigonometric function of } x \text{"} = \text{a number}\)
we can use the following strategy to solve the equation:
- Find all solutions of the equation within one period of the function. This is often done by using properties of the trigonometric function. Quite often, there will be two solutions within a single period.
- Use the period of the function to express formulas for all solutions by adding integer multiples of the period to each solution found in the first step. For example, if the function has a period of \(2\pi\) and \(x_{1}\) and \(x_{2}\) are the only two solutions in a complete period, then we would write the solutions for the equation as \[x = x_{1} + k(2\pi), x = x_{2} + k(2\pi)\] where \(k\) is an integer:
We can sometimes use trigonometric identities to help rewrite a given equation in the form of equation (1).


