4.3: Sum and Difference Identities
- Page ID
- 7120
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- What are the Cosine Difference and Sum Identities?
- What are the Sine Difference and Sum Identities?
- What are the Tangent Difference and Sum Identities?
- What are the Cofunction Identities?
- Why are the difference and sum identities useful?
The next identities we will investigate are the sum and difference identities for the cosine and sine. These identities will help us find exact values for the trigonometric functions at many more angles and also provide a means to derive even more identities.
Beginning Activity
- Is \(\cos(A - B) = \cos(A) - \cos(B)\) an identity? Explain.
- Is \(\sin(A - B) = \sin(A) - \sin(B)\) an identity? Explain.
- Use a graphing utility to draw the graph of \(y = \sin(\dfrac{\pi}{2} - x)\) and \(y = \cos(x)\) over the interval \([-2\pi, 2\pi]\) on the same set of axes. Do you think \(y = \sin(\dfrac{\pi}{2} - x) = \cos(x)\) is an identity? Why or why not?
The Cosine Difference Identity
To this point we know the exact values of the trigonometric functions at only a few angles. Trigonometric identities can help us extend this list of angles at which we know exact values of the trigonometric functions. Consider, for example, the problem of finding the exact value of \(\cos(\dfrac{\pi}{12})\). The definitions and identities we have so far do not help us with this problem. However, we could notice that \(\dfrac{\pi}{12} = \dfrac{\pi}{3} - \dfrac{\pi}{4}\) and if we knew how the cosine behaved with respect to the difference of two angles, then we could find \(\cos(\dfrac{\pi}{12})\). In our Beginning Activity, however, we saw that the equation \(\cos(A - B) = \cos(A) - \cos(B)\) is not an identity, so we need to understand how to relate \(\cos(A - B)\) to cosines and sines of \(A\) and \(B\).
We state the Cosine Difference Identity below. This identity is not obvious, and a verification of the identity is given later in this section. For now we focus on using the identity.
Cosine Difference Identity
For any real numbers \(A\) and \(B\) we have \[\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]
Example \(\PageIndex{1}\): (Using the Cosine Difference Identity)
Let us return to our problem of finding \(\cos(\dfrac{\pi}{12})\). Since we know \(\dfrac{\pi}{12} = \dfrac{\pi}{3} - \dfrac{\pi}{4}\), we can use the Cosine Difference Identity with \(A = \dfrac{\pi}{3}\) and \(B = \dfrac{\pi}{4}\) to obtain
\[\cos(\dfrac{\pi}{12}) = \cos(\dfrac{\pi}{3} - \dfrac{\pi}{4}) = \cos(\dfrac{\pi}{3})\cos(\dfrac{\pi}{4}) + \sin(\dfrac{\pi}{3}\sin(\dfrac{\pi}{4})) = (\dfrac{1}{2})(\dfrac{\sqrt{2}}{2}) + (\dfrac{\sqrt{3}}{2})(\dfrac{\sqrt{2}}{2}) = \dfrac{\sqrt{2}+\sqrt{6}}{4}.\]
So we see that \(\cos(\dfrac{\pi}{12}) = \dfrac{\sqrt{2}+\sqrt{6}}{4}.\)
Exercise \(\PageIndex{1}\)
- Determine the exact value of \(\cos(\dfrac{7\pi}{12})\) using the Cosine Difference Identity
- Given that \(\dfrac{5\pi}{12} = \dfrac{\pi}{6} + \dfrac{\pi}{4} = \dfrac{\pi}{6} - (-\dfrac{\pi}{4})\), determine the exact value of \(\cos(\dfrac{5\pi}{12})\) using the Cosine Difference Identity.
- Answer
-
1. We first note that \(\dfrac{7\pi}{12} = \dfrac{9\pi}{12} - \dfrac{2\pi}{6} = \dfrac{3\pi}{4} - \dfrac{\pi}{6}\).
\[\cos(\dfrac{7\pi}{12}) = \cos(\dfrac{}{})\]
2.
\[\cos(\dfrac{5\pi}{12}) = \cos(\dfrac{\pi}{6} - (-\dfrac{\pi}{4})) = \cos(\dfrac{\pi}{6})\cos(\dfrac{\pi}{4}) + \sin(\dfrac{\pi}{6})\sin(-\dfrac{\pi}{4}) = (\dfrac{\sqrt{3}}{2})(\dfrac{\sqrt{2}}{2}) + (\dfrac{1}{2})(-\dfrac{\sqrt{2}}{2}) = \dfrac{\sqrt{6} - \sqrt{2}}{4}\]
The Cosine Sum Identity
Since there is a Cosine Difference Identity, we might expect there to be a Cosine Sum Identity. We can use the Cosine Difference Identity along with the negative identities to find an identity for \(\cos(A + B)\). The basic idea was contained in our last Progress Check, where we wrote \(A + B\) as \(A - (-B)\). To see how this works in general, notice that
\[\cos(A + B) = \cos(A - (-B)) = \cos(A)\cos(-B) + \sin(A)\sin(-B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]
This is the Cosine Sum Identity.
Cosine Sum Identity
For any real numbers \(A\) and \(B\) we have
\[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]
Exercise \(\PageIndex{2}\)
- Find a simpler formula for \(\cos(\pi + x)\) in terms of \(\cos(x)\). Illustrate with a graph.
- Use the Cosine Difference Identity to prove that \(\cos(\dfrac{\pi}{2} - x) = \sin(x)\) is an identity.
- Answer
-
1. \(\cos(\pi + x) = \cos(\pi)\cos(x) - \sin(\pi)\sin(x) = -\cos(x)\). The graphs of \(y = \cos(\pi + x)\) and \(y = \cos(x)\) are indentical.
2. \(\cos(\dfrac{\pi}{2} - x) = \cos(\dfrac{\pi}{2})\cos(x) + \sin(\dfrac{\pi}{2})\sin(x) = 0\cdot \cos(x) + 1\cdot \sin(x)\). So we see that \(\cos(\dfrac{\pi}{2} - x) = \sin(x)\)
Cofunction Identities
In Progress Check 4.14 we used the Cosine Difference Identity to see that \(\cos(\dfrac{\pi}{2} - x) = \sin(x)\) is an identity. Since this is an identity, we can replace \(x\) with \(\dfrac{\pi}{2} - x\) to see that
\[\sin(\dfrac{\pi}{2} - x) = \cos(\dfrac{\pi}{2} - (\dfrac{\pi}{2} - x)) = \cos(x),\]
so \[\sin(\dfrac{\pi}{2} - x) = \cos(x),\]. The two identities
\[\cos(\dfrac{\pi}{2} - x) = \sin(x)\] and \[\sin(\dfrac{\pi}{2} - x) = \cos(x)\]
are called cofunction identities. These two cofunction identities show that the sine and cosine of the acute angles in a right triangle are related in a particular way.
Since the sum of the measures of the angles in a right triangle is \(\pi\) radians or \(180^\circ\), the measures of the two acute angles in a right triangle sum to \(\dfrac{\pi}{2}\) radians or \(90^\circ\). Such angles are said to be complementary. Thus, the sine of an acute angle in a right triangle is the same as the cosine of its complementary angle. For this reason we call the sine and cosine cofunctions. The naming of the six trigonometric functions reflects the fact that they come in three sets of cofunction pairs: the sine and cosine, the tangent and cotangent, and the secant and cosecant. The cofunction identities are the same for any cofunction pair.
Cofunction Identities
For any real number x for which the expressions are defined,
- \(\cos(\dfrac{\pi}{2} - x) = \sin(x)\)
- \(\sin(\dfrac{\pi}{2} - x) = \cos(x)\)
- \(\tan(\dfrac{\pi}{2} - x) = \cot(x)\)
- \(\cot(\dfrac{\pi}{2} - x) = \tan(x)\)
- \(\sec(\dfrac{\pi}{2} - x) = \csc(x)\)
- \(\csc(\dfrac{\pi}{2} - x) = \sec(x)\)
For any angle \(x\) in degrees for which the functions are defined,
- \(\cos(90^\circ - x) = \sin(x)\)
- \(\sin(90^\circ - x) = \cos(x)\)
- \(\tan(90^\circ- x) = \cot(x)\)
- \(\cot(90^\circ - x) = \tan(x)\)
- \(\sec(90^\circ - x) = \csc(x)\)
- \(\csc(90^\circ - x) = \sec(x)\)
Exercise \(\PageIndex{3}\)
Use the cosine and sine cofuntion identities to prove the cofunction identity \[\tan(90^\circ- x) = \cot(x)\]
- Answer
-
We will use the identity \(\tan(y) = \dfrac{\sin(y)}{\cos(y)}\).
\[\tan(\dfrac{\pi}{2} - x) = \dfrac{\sin(\dfrac{\pi}{2} - x)}{\cos(\dfrac{\pi}{2} - x)} = \dfrac{\cos(x)}{\sin(x)} = \cot(x)\]
The Sine Difference and Sum Identities
We can now use the Cosine Difference Identity and the Cofunction Identities to derive a Sine Difference Identity:
\[\sin(A - B) = \cos(\dfrac{\pi}{2} - (A - B)) = \cos((\dfrac{\pi}{2} - A) + B)) = \cos(\dfrac{\pi}{2} - A)\cos(B) - \sin(\dfrac{\pi}{2} - A)\sin(B)= \sin(A)\cos(B) - \cos(A)\sin(B).\]
We can derive a Sine Sum Identity from the Sine Difference Identity:
\[\sin(A + B) = \sin(A - (-B)) = \sin(A)\cos(-B) - \cos(A)\sin(-B) = \sin(A)\cos(B) + \cos(A)\sin(B)\]
Sine Difference and Sum Identities
For any real numbers \(A\) and \(B\) we have
\[\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\] and \[\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)\]
Exercise \(\PageIndex{4}\)
Use the Sine Sum or Difference Identities to find the exact values of the following.
- \[\sin(\dfrac{\pi}{12})\]
- \[\sin(\dfrac{5\pi}{12})\]
- Answer
-
1. We note that \(\dfrac{\pi}{12} = \dfrac{\pi}{3} - \dfrac{\pi}{4}\).
\[\sin(\dfrac{\pi}{12}) = \sin(\dfrac{\pi}{3} - \dfrac{\pi}{4}) = \sin(\dfrac{\pi}{3})\cos(\dfrac{\pi}{4}) - \cos(\dfrac{\pi}{3})\sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{3}}{2}\cdot \dfrac{\sqrt{2}}{2} - \dfrac{1}{2}\cdot \dfrac{\sqrt{2}}{2} = \dfrac{\sqrt{6} - \sqrt{2}}{4}\]
2. We note that \(\dfrac{5\pi}{12} = \dfrac{\pi}{4} + \dfrac{\pi}{6}\).
\[\sin(\dfrac{5\pi}{12}) = \dfrac{\pi}{4} + \dfrac{\pi}{6} = \sin(\dfrac{\pi}{4})\cos(\dfrac{\pi}{6}) + \cos(\dfrac{\pi}{4})\sin(\dfrac{\pi}{6}) = \dfrac{\sqrt{2}}{2}\cdot \dfrac{\sqrt{3}}{2} + \dfrac{\sqrt{2}}{2}\cdot \dfrac{1}{2} = \dfrac{\sqrt{6} + \sqrt{2}}{4}\]
Using Sum and Difference Identities to Solve Equations
As we have done before, we can use our new identities to solve other types of trigonometric equations.
Example \(\PageIndex{2}\): (Using the Cosine Sum Identity to Solve an Equation)
Consider the equation
\[\cos(\theta)\cos(\dfrac{\pi}{5}) - \sin(\theta)\sin(\dfrac{\pi}{5}) = \dfrac{\sqrt{3}}{2}\]
On the surface this equation looks quite complicated, but we can apply an identity to simplify it to the point where it is straightforward to solve. Notice that left side of this equation has the form \(\cos(A)\cos(B) - \sin(A)\sin(B)\) with \(A = \theta\) and \(B = \dfrac{\pi}{5}\)
We can use the Cosine Sum Identity \(\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\) to combine the terms on the left into a single term, and we can solve the equation from there:
\[\cos(\theta)\cos(\dfrac{\pi}{5}) - \sin(\theta)\sin(\dfrac{\pi}{5}) = \dfrac{\sqrt{3}}{2}\]
\[\cos(\theta + \dfrac{\pi}{5}) = \dfrac{\sqrt{3}}{2}\]
Now \(\cos(x) =\dfrac{\sqrt{3}}{2}\) when \(x = \dfrac{\pi}{6} + 2k\pi\) or \(x = -\dfrac{\pi}{6} + 2k\pi\) for integers \(k\). Thus, \(\cos(\theta + \dfrac{\pi}{5}) = \dfrac{\sqrt{3}}{2}\) when \(\theta + \dfrac{\pi}{5} = \dfrac{\pi}{6} + 2k\pi\) or \(\theta + \dfrac{\pi}{5} = -\dfrac{\pi}{6} + 2k\pi\). Solving for \(\theta\) gives us the solutions
\[\theta = -\dfrac{\pi}{30} + 2k\pi\] or \[\theta = -\dfrac{11\pi}{30} + 2k\pi\]
where \(k\) is any integer. These solutions are illustrated in Figure \(\PageIndex{1}\).
Note
Up to now, we have been using the phrase “Determine formulas that can be used to generate all the solutions of a given equation.” This is not standard terminology but was used to remind us of what we have to do to solve a trigonometric equation. We will now simply say, “Determine all solutions for the given equation.” When we see this, we should realize that we have to determine formulas that can be used to generate all the solutions of a given equation.
Exercise \(\PageIndex{5}\)
Determine all solutions of the equation
\[\sin(x)\cos(1) + \cos(x)\sin(1) = 0.2\]
Hint: Use a sum or difference identity and use the inverse sine function.
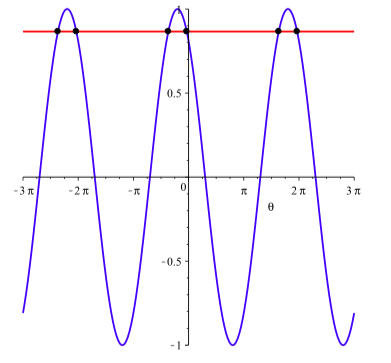
Figure \(\PageIndex{1}\): Graphs of \(y = \cos(\theta)\cos(\dfrac{\pi}{5}) - \sin(\theta)\sin(\dfrac{\pi}{5})\) and \(y = \dfrac{\sqrt{3}}{2}\)
- Answer
-
We first use the Sine Sum Identity to rewrite the equation as \(\sin(x + 1) = 0.2\). If we let \(t = x + 1\), we see that for \(0 \leq t < 2\pi\),
\[t = \arcsin(0.2)\] or \[t = (\pi - \arcsin(0.2))\]
So we have \(x + 1 = \arcsin(0.2)\) or \(x + 1 = \pi - \arcsin(0.2)\). Since the period of the functions we are working with is \(2\pi\), we see that
\[x = (-1 + \arcsin(0.2)) + k(2\pi)\] or \[x = (-1 + \pi - \arcsin(0.2)) + k(2\pi)\]where \(k\) is an integer.
Appendix – Proof of the Cosine Difference Identity
To understand how to calculate the cosine of the difference of two angles, let \(A\) and \(B\) be arbitrary angles in radians. Figure 4.7 shows these angles with \(A > B\), but the argument works in general. If we plot the points where the terminal sides of the angles \(A\), \(B\) and \(A - B\) intersect the unit circle, we obtain the picture in Figure 4.7.
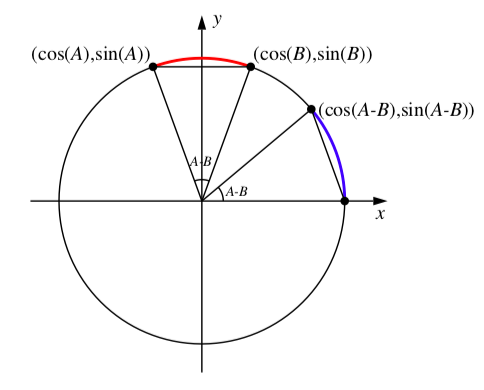
Figure \(\PageIndex{2}\): The cosine difference formula
The arc on the unit circle from the point \((\cos(B), \sin(B))\) to the point \((\cos(A), \sin(A))\) has length \(A - B\) and the arc from the point \((1, 0)\) to the point \((\cos(A - B), \sin(A - B))\) also has length \(A - B\). So the chord from \((\cos(B), \sin(B))\) to \((\cos(A), \sin(A))\) has the same length as the chord from (1,0) to \((\cos(A - B), \sin(A - B))\). To find the cosine difference formula, we calculate these two chord lengths using the distance formula.
The length of the chord from \((\cos(B), \sin(B))\) to \((\cos(A), \sin(A))\) is
\[\sqrt{(\cos(A) - \cos(B))^{2} + (\sin(A) - \sin(B))^{2}}\]
and the length of the chord from \((1, 0)\) to the point \((\cos(A - B), \sin(A - B))\) is
\[\sqrt{(\cos(A - B) - 1)^{2} + (\sin(A - B) - 0)^{2}}\]
Since these two chord lengths are the same we obtain the equation
\[\sqrt{(\cos(A - B) - 1)^{2} + (\sin(A - B) - 0)^{2}} = \sqrt{(\cos(A) - \cos(B))^{2} + (\sin(A) - \sin(B))^{2}}\]
The cosine difference identity is found by simplifying Equation (2) by first squaring both sides:
\[(\cos(A - B) - 1)^{2} + (\sin(A - B) - 0)^{2} = (\cos(A) - \cos(B))^{2} + (\sin(A) - \sin(B))^{2}\]
Then we expand both sides
\[[\cos^{2}(A - B) - 2\cos(A - B) + 1] + \sin^{2}(A - B) = [\cos^{2}(A) - 2\cos(A)\cos(B) + \cos^{2}(B)] + [\sin^{2}(A) - 2\sin(A)\sin(B) + \sin^{2}(B)]\]
We can combine some like terms:
\[[\cos^{2}(A - B) + \sin^{2}(A - B)] - 2\cos(A - B) + 1 = [\cos^{2}(A) + \sin^{2}(A)] + [\cos^{2}(B) + \sin^{2}(B)] - 2\sin(A)\sin(B) - 2\cos(A)\cos(B)]\]
Finally, using the Pythagorean identities yields
\[1 - 2\cos(A - B) + 1 = 1 + 1 - 2\cos(A)\cos(B) - 2\sin(A)\sin(B)\]
\[- 2\cos(A - B) = - 2\cos(A)\cos(B) - 2\sin(A)\sin(B)\]
\[\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]
Summary
In this section, we studied the following important concepts and ideas:
- Sum and Difference Identities
\[\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]
\[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]
\[\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\]
\[\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)\] - Cofunction Identities
See page 266 for a list of the cofunction identities.


