4.E: Trigonometric Identities and Equations (Exercises)
- Page ID
- 17331
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise \(\PageIndex{1}\)
Use a graphing utility to graph each side of the given equation. If the equation appears to be an identity, prove the identity. If the equation appears to not be an identity, demonstrate one input at which the two sides of the equation have different values. Remember that when proving an identity, work to transform one side of the equation into the other using known identities. Some general guidelines are
- Begin with the more complicated side.
- It is often helpful to use the definitions to rewrite all trigonometric functions in terms of the cosine and sine.
- When appropriate, factor or combine terms. For example, \(\sin^{2}(x) + \sin(x)\) can be written as \(\sin(x)(\sin(x) + 1)\) and \(\dfrac{1}{\sin(x)} + \dfrac{1}{\cos(x)}\) can be written as the single fraction \(\dfrac{\cos(x) + \sin(x)}{\sin(x)\cos(x)}\) with a common denominator.
- As you transform one side of the equation, keep the other side of the equation in mind and use identities that involve terms that are on the other side. For example, to verify that \(\tan^{2}(x) + 1 = \dfrac{1}{\cos^{2}(x)}\), start with\(\tan^{2}(x) + 1\) and make use identities that relate \(\tan(x)\) to \(\cos(x)\) as closely as possible.
\[\cos(x)\tan(x) = \sin(x)\]
\[\dfrac{\cot(s)}{\csc(s)} = \cos(s)\]
\[\dfrac{\tan(s)}{\sec(s)} = \sin(s)\]
\[\cos^{2}(x) + 1 = \csc^{2}(x)\]
\[\sec^{2}(x) + \csc^{2}(x) = 1\]
\[\cot(t) + 1 = \csc(t)(\cos(t) + \sin(t))\]
\[\tan^{2}(\theta)(1 + \cot^{2}(\theta)) = \dfrac{1}{1 - \sin^{2}(\theta)}\]
\[\dfrac{1 - \sin^{2}(\beta)}{\cos(\beta)} = \sin(\beta)\]
\[\dfrac{1 - \sin^{2}(\beta)}{\cos(\beta)} = \cos(\beta)\]
\[\sin^{2}(x) + \tan^{2}(x) + \cos^{2}(x) = \sec^{2}(x)\]
- Answer
-
(a) \(\cos(x)\tan(x) = \cos(x)\dfrac{\sin(x)}{\cos(x)} = \sin(x)\)
(b) \(\dfrac{\cot(x)}{(x)} = \dfrac{\dfrac{\cos(x)}{\sin(x)}}{\dfrac{1}{\sin(x)}} = \dfrac{\cos(x)}{\sin(x)} \times \dfrac{\sin{x}}{1} = \cos(x)\)
(e) A graph will show that this is not an identity. In particular, we see that \[\sec^{2}(\dfrac{\pi}{4}) + \csc^{2}(\dfrac{\pi}{4}) = (\sqrt{2})^{2} + (\sqrt{2})^{2} = 4\]
Exercise \(\PageIndex{2}\)
A student claims that \(\cos(\theta) + \sin(\theta) = 1\) is an identity because \(\cos(0) + \sin(0) = 1 + 0 = 0\). How would you respond to this student?
Exercise \(\PageIndex{3}\)
If a trigonometric equation has one solution, then the periodicity of the trigonometric functions implies that the equation will have infinitely many solutions. Suppose we have a trigonometric equation for which both sides of the equation are equal at infinitely many different inputs. Must the equation be an identity? Explain your reasoning
Exercise \(\PageIndex{4}\)
For each of the following equations, determine formulas that can be used to generate all solutions of the given equation. Use a graphing utility to graph each side of the given equation to check your solutions.
\[2\sin(x) - 1 = 0\]
\[2\cos(x) + 1 = 0\]
\[2\sin(x) + \sqrt{2} = 0\]
\[4\cos(x) - 3 = 0\]
\[3\sin^{2}(x) - 2\sin(x) = 0\]
\[\sin(x)\cos^{2}(x) = 2\sin(x)\]
\[\cos^{2}(x) + 4\sin(x) = 4\]
\[5\cos(x) + 4 = 2\sin^{2}(x)\]
\[3\tan^{2}(x) - 1 = 0\]
\[\tan^{2}(x) - \tan(x) = 6\]
- Answer
-
(a) \(x = \dfrac{\pi}{6} + k(2\pi)\) or \(x = \dfrac{5\pi}{6} + k(2\pi)\), where \(k\) is an integer.
(b) \(x = \dfrac{2\pi}{3} + k(2\pi)\) or \(x = \dfrac{4\pi}{3} + k(2\pi)\), where \(k\) is an integer.
(d) \(x = \cos^{-1}(\dfrac{3}{4} + k(2\pi)\) or \(x = \cos^{-1}(-\dfrac{3}{4} + k(2\pi)\), where \(k\) is an integer.
(f) \(x = k\pi\), where \(k\) is an integer.
Exercise \(\PageIndex{5}\)
A student is asked to approximate all solutions in degrees (to two decimal places) to the equation \(\sin(\theta) + \dfrac{1}{3} = 1\) on the interval \(0^\circ \leq \theta \leq 360^\circ\).The student provides the answer \(\theta = \sin^{-1}(\dfrac{2}{3}) \approx 41.81^\circ\). Did the student provide the correct answer to the stated problem? Explain.
- Answer
-
\(\theta = \sin^{-1}(\dfrac{2}{3}) \approx 41.81^\circ\) is one solution of the equation \(\sin(\theta) + \dfrac{1}{3} = 1\) with \(0 \leq \theta \leq 360^\circ\). There is another solution (in the second quadrant) for this equation with \(0 \leq \theta \leq 360^\circ\).
Exercise \(\PageIndex{6}\)
X-ray crystallography is an important tool in chemistry. One application of X-ray crystallography is to discover the atomic structure macromolecules. For example, the double helical structure of DNA was found using X-ray crystallography.
The basic idea behind X-ray crystallography is this: two X-ray beams with the same wavelength \(\lambda\) and phase are directed at an angle \(\theta\) toward a crystal composed of atoms arranged in a lattice in planes separated by a distance \(d\) as illustrated in Figure4.5.1 The beams reflect off different atoms (labeled as \(P\) and \(Q\) in Figure 4.5) within the crystal. One X-ray beam (the lower one as illustrated in Figure 4.5) must travel a longer distance than the other. When reflected, the X-rays combine but, because of the phase shift of the lower beam, the combination might have a small amplitude or a large amplitude. Bragg’s Law states that the sum of the reflected rays will have maximum amplitude when the extra length the longer beam has to travel is equal to an integer multiple of the wavelength \(\lambda\) of the radiation. In other words, \[n\lambda = 2d\sin(\theta),\]
for some positive integer \(n\). Assume that \(\lambda = 1.54\) angstroms and \(d = 2.06\) angstroms. Approximate to two decimal places the smallest value of \(\theta\) (in degrees) for which \(n = 1\).
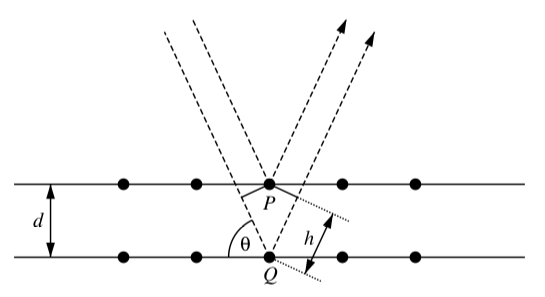
Figure \(\PageIndex{1}\): X-rays reflected from crystal atoms.
Exercise \(\PageIndex{7}\)
Use an appropriate sum or difference identity to find the exact value of each of the following.
- \(\cos(-10^\circ)\cos(35^\circ) + \sin(-10^\circ)\sin(35^\circ)\)
- \(\cos(\dfrac{7\pi}{9})\cos(\dfrac{2\pi}{9}) - \sin(\dfrac{7\pi}{9})\sin(\dfrac{2\pi}{9}))\)
- \(\sin(\dfrac{7\pi}{9})\cos(\dfrac{2\pi}{9}) + \cos(\dfrac{7\pi}{9})\sin(\dfrac{2\pi}{9}))\)
- \(\sin(80^\circ)\cos(55^\circ) + \cos(80^\circ)\sin(55^\circ)\)
- Answer
-
- \(\cos(-10^\circ - 35^\circ) = \cos(-45^\circ) = \dfrac{\sqrt{2}}{2}\).
- \(\cos(\dfrac{7\pi}{9} + \dfrac{2\pi}{9}) = \cos(\pi) = -1\)
Exercise \(\PageIndex{8}\)
Angles \(A\) and \(B\) are in standard position and \(\sin(\dfrac{1}{2}, \cos(A) > 0)\), \(\cos(B) = \dfrac{3}{4}\), and \(\sin(B) < 0\). Draw a picture of the angles \(A\) and \(B\) in the plane and then find each of the following.
- \(\cos(A + B)\)
- \(\cos(A - B)\)
- \(\sin(A + B)\)
- \(\sin(A - B)\)
- \(\tan(A + B)\)
- \(\tan(A - B)\)
- Answer
-
We first use the Pythagorean Identity to determine \(\cos(A)\) and \(\sin(B)\). From this, we get \[\cos(A) = \dfrac{\sqrt{3}}{2}\] and \[\sin(B) = -\dfrac{\sqrt{7}}{4}\]
(a) \[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B) = \dfrac{\sqrt{3}}{2}\cdot\dfrac{3}{4} - \dfrac{1}{2}\cdot(-\dfrac{\sqrt{7}}{4}) = \dfrac{3\sqrt{3} + \sqrt{7}}{8}\]
Exercise \(\PageIndex{9}\)
Identify angles \(A\) and \(B\) at which we know the values of the cosine and sine so that a sum or difference identity can be used to calculate the exact value of the given quantity. (For example, \(15^\circ = 45^\circ - 30^\circ\).)
- \(\cos(15^\circ)\)
- \(\sin(75^\circ)\)
- \(\tan(105^\circ)\)
- \(\sec(345^\circ)\)
- Answer
-
(a) \(\cos(15^\circ) = \cos(45^\circ - 30^\circ) = \dfrac{\sqrt{6} + \sqrt{2}}{4}\)
(b) We can use \(345^\circ = 300^\circ + 45^\circ\) and first evaluate \(\cos(345^\circ)\). This gives \(\cos(345^\circ) = \dfrac{\sqrt{6} + \sqrt{2}}{4}\) and \(\sec(345^\circ) = \dfrac{4}{\sqrt{6} + \sqrt{2}}\). We could have also used the fact that \(\cos(345^\circ) = \cos(15^\circ)\) and the result in part (a).
Exercise \(\PageIndex{10}\)
Verify the sum and difference identities for the tangent:
\[\tan(A - B) = \dfrac{\tan(A) - \tan(B)}{1 + \tan(A)\tan(B)}\] and
\[\tan(A + B) = \dfrac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)}\]
Exercise \(\PageIndex{11}\)
Verify the cofunction identities
- \(\cot(\dfrac{\pi}{2} - x) = \tan(x)\)
- \(\sec(\dfrac{\pi}{2} - x) = \csc(x)\)
- \(\csc(\dfrac{\pi}{2} - x) = \sec(x)\)
- Answer
-
(a) \[\cot(\dfrac{\pi}{2} - x) = \dfrac{\cos(\dfrac{\pi}{2} - x)}{\sin(\dfrac{\pi}{2} - x)} = \dfrac{\sin(x)}{\cos(x)} = \tan(x)\]
Exercise \(\PageIndex{12}\)
Draw graphs to determine if a given equation is an identity. Verify those equations that are identities and provide examples to show that the others are not identities.
- \(\sin(x + \dfrac{\pi}{4}) + \sin(x - \dfrac{\pi}{4}) = 2\sin(x)\cos(\dfrac{\pi}{4})\)
- \(\sin(210^\circ + x) - \cos(210^\circ + x) = 0\)
Exercise \(\PageIndex{13}\)
Determine if the following equations are identities.
- \(\dfrac{\sin(r + s)}{\cos(r)\cos(s)} = \tan(r) + \tan(s)\)
- \(\dfrac{\sin(r - s)}{\cos(r)\cos(s)} = \tan(r) - \tan(s)\)
Exercise \(\PageIndex{14}\)
Use an appropriate identity to solve the given equation.
- \(\sin(\theta)\cos(35^\circ) = \cos(\theta)\sin(35^\circ) = \dfrac{1}{2}\)
- \(\cos(2x)\cos(x) = \sin(2x)\sin(x) = -1\)
Exercise \(\PageIndex{15}\)
- Use a graphing device to draw the graph of \(f(x) = \sin(x) + \cos(x)\) using \(-\pi \leq x \leq 2\pi\) and \(-2 \leq y \leq 2\). Does the graph of this function appear to be a sinusoid? If so, approximate the amplitude and phase shift of the sinusoid. What is the period of this sinusoid.
- Use one of the sum identities to rewrite the expression \(\sin(x + \dfrac{\pi}{4})\). Then use the values of \(\sin(\dfrac{\pi}{4})\) and \(\cos(\dfrac{\pi}{4})\) to further rewrite the expression.
- Use the result from part(b) to show that the function \(f(x) = \sin(x) + \cos(x)\) is indeed a sinusoidal function. What is its amplitude, phase shift, and period?
Exercise \(\PageIndex{16}\)
- Use a graphing device to draw the graph of \(g(x) = \sin(x) + \sqrt{3}\cos(x)\) using \(-\pi \leq x \leq 2\pi\) and \(-2.5 \leq y \leq 2.5\). Does the graph of this function appear to be a sinusoid? If so, approximate the amplitude and phase shift of the sinusoid. What is the period of this sinusoid.
- Use one of the sum identities to rewrite the expression \(\sin(x + \dfrac{\pi}{3})\). Then use the values of \(\sin(\dfrac{\pi}{3})\) and \(\cos(\dfrac{\pi}{3})\) to further rewrite the expression.
- Use the result from part(b) to show that the function \(g(x) = \sin(x) + \sqrt{3}\cos(x)\) is indeed a sinusoidal function. What is its amplitude, phase shift, and period?
Exercise \(\PageIndex{17}\)
When two voltages are applied to a circuit, the resulting voltage in the circuit will be the sum of the individual voltages. Suppose two voltages \(V_{1}(t) = 30\sin(120\pi t)\) and \(V_{2}(t) = 40\cos(120\pi t)\) are applied to a circuit. The graph of the sum \(V(t) = V_{1}(t) + V_{2}(t)\) is shown in Figure 4.8.
- Use the graph to estimate the values of \(C\) so that \[y = 50\sin(120\pi(t - c))\] fits the graph of \(V\).
- Use the Sine Difference Identity to rewrite \(50\sin(120\pi(t - c))\) as an expression of the form \(50\sin(A)\cos(B) - 50\cos(A)\sin(B)\) where \(A\) and \(B\) involve \(t\) and/or \(C\). From this, determine a value of C that will make
\[30\sin(120\pi t) + 40\cos(120\pi t) = 50\sin(120\pi(t - c))\].Compare this value of \(C\) to the one you estimated in part (a).
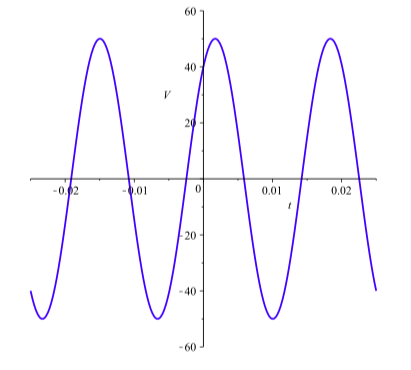
Figure \(\PageIndex{2}\): Graph of \(V(t) = V_{1}(t) + V_{2}(t)\).
Exercise \(\PageIndex{18}\)
Given that \(\cos(\theta) = \dfrac{2}{3})\) and \(\sin(\theta) < 0\), determine the exact values of \(\sin(2\theta)\), \(\cos(2\theta)\), and \(\tan(2\theta)\).
- Answer
-
Use the Pythagorean Identity to obtain \(\sin^{2}(\theta) = \dfrac{5}{9}\). Since \(\sin(\theta) < 0\), we see that \(\sin(\theta) = -\dfrac{\sqrt{5}}{3}\). Now use appropriate double angle identities to get \[\sin(2\theta) = -\dfrac{4\sqrt{5}}{9}\] \[\cos(2\theta) = -\dfrac{1}{9}\]
Then use \(\tan(2\theta) = \dfrac{\sin(2\theta)}{\cos(2\theta)} = 4\sqrt{5}\).
Exercise \(\PageIndex{19}\)
Find all solutions to the given equation. Use a graphing utility to graph each side of the given equation to check your solutions.
- \(\cos(x)\sin(x) = \dfrac{1}{2}\)
- \(\cos(2x) + 3 = 5\cos(x)\)
- Answer
-
(a) \(x = \dfrac{\pi}{4} + k\pi\), where \(k\) is an integer.
Exercise \(\PageIndex{20}\)
Determine which of the following equations is an identity. Verify your responses.
- \(\cot(t)\sin(2t) = 1 + \cos(2t)\)
- \(\sin(2x) = \dfrac{2 - \csc^{2}(x)}{\csc^{2}(x)}\)
- \(\cos(2x) = \dfrac{2 - \sec^{2}(x)}{\sec^{2}(x)}\)
- Answer
-
(a) This is an identity. Start with the left side of the equation and use \(\cot(t) = \dfrac{\cos(t)}{\sin(t)}\) and \(\sin(2t) = 2\sin(t)\cos(t)\).
Exercise \(\PageIndex{21}\)
Find a simpler formula for \(\cos(\pi + x)\) in terms of \(\cos(x)\). Illustrate with a graph.
Exercise \(\PageIndex{22}\)
A classmate shares his solution to the problem of solving \(\sin(2x) = 2\cos(x)\) over the interval \([0, 2\pi)\). He has written
\[\sin(2x) = 2\cos(x)\]
\[\dfrac{\sin(2x)}{2} = \cos(x)\]
\[\sin(x) = \cos(x)\]
\[\tan(x) = 1\]
so \(x = \dfrac{\pi}{4}\) or \(x = \dfrac{5\pi}{4}\)
- Draw graphs of \(\sin(2x)\) and \(2\cos(x)\) and explain why this classmates
- Find the error in this classmate’s argument.
- Determine the solutions to \(\sin(2x) = 2\cos(x)\) over the interval \([0, 2\pi)\).
Exercise \(\PageIndex{23}\)
Determine the exact value of each of the following:
- \(\sin(22.5^\circ)\)
- \(\cos(22.5^\circ)\)
- \(\tan(22.5^\circ)\)
- \(\sin(15^\circ)\)
- \(\cos(15^\circ)\)
- \(\tan(15^\circ)\)
- \(\sin(195^\circ)\)
- \(\cos(195^\circ)\)
- \(\tan(195^\circ)\)
- Answer
-
(a) \(\sin(22.5^\circ) = \sqrt{\dfrac{1 - \dfrac{\sqrt{2}}{2}}{2}} = \dfrac{1}{2}\sqrt{2 - \sqrt{2}}\).
(c) \(\tan(22.5^\circ) = \sqrt{\dfrac{2 - \sqrt{2}}{2 + \sqrt{2}}} = \sqrt{3 - 2\sqrt{2}}\)
(h) \(\cos(195^\circ) = -\sqrt{\dfrac{1 + \dfrac{\sqrt{3}}{2}}{2}} = -\dfrac{1}{2}\sqrt{2 + \sqrt{3}}\)
Exercise \(\PageIndex{24}\)
Determine the exact value of each of the following:
- \(\sin(\dfrac{3\pi}{8})\)
- \(\cos(\dfrac{3\pi}{8})\)
- \(\tan(\dfrac{3\pi}{8})\)
- \(\sin(\dfrac{5\pi}{8})\)
- \(\cos(\dfrac{5\pi}{8})\)
- \(\tan(\dfrac{5\pi}{8})\)
- \(\sin(\dfrac{11\pi}{12})\)
- \(\cos(\dfrac{11\pi}{12})\)
- \(\tan(\dfrac{11\pi}{12})\)
- Answer
-
(a) \(\sin(\dfrac{3\pi}{8}) = \sqrt{\dfrac{1 + \dfrac{\sqrt{2}}{2}}{2}} = \dfrac{1}{2}\sqrt{2 + \sqrt{2}}\)
(c) \(\tan(\dfrac{3\pi}{8}) = \sqrt{\dfrac{2 + \sqrt{2}}{2 - \sqrt{2}}} = \sqrt{3 + 2\sqrt{2}}\)
(h) \(\cos(\dfrac{11\pi}{12}) = -\sqrt{\dfrac{1 + \dfrac{\sqrt{3}}{2}}{2}} = -\dfrac{1}{2}\sqrt{2 + \sqrt{3}}\)
Exercise \(\PageIndex{25}\)
If \(\cos(x) = \dfrac{2}{3}\) and \(\sin(x) < 0\) and \(0 \leq x \leq 2\pi\), determine the exact value of each of the following:
- \(\cos(\dfrac{x}{2})\)
- \(\sin(\dfrac{x}{2})\)
- \(\tan(\dfrac{x}{2})\)
- Answer
-
(a) We note that since \(\dfrac{3\pi}{2} \leq x \leq 2\pi, \dfrac{3\pi}{4} \leq \dfrac{x}{2} \leq \pi\).
\[\sin(\dfrac{x}{2}) = \sqrt{\dfrac{1 - \dfrac{2}{3}}{2}} = \dfrac{1}{\sqrt{6}}\]
Exercise \(\PageIndex{26}\)
If \(\sin(x) = \dfrac{2}{5}\) and \(\cos(x) < 0\) and \(0 \leq x \leq 2\pi\), determine the exact value of each of the following:
- \(\cos(\dfrac{x}{2})\)
- \(\sin(\dfrac{x}{2})\)
- \(\tan(\dfrac{x}{2})\)
Exercise \(\PageIndex{27}\)
A rectangle is inscribed in a semicircle of radius \(r\) as shown in the diagram as follows.
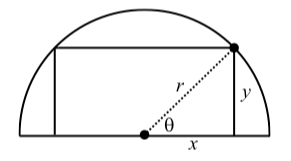
Figure \(\PageIndex{3}\)
We can write the area \(A\) of this rectangle as \(A = (2x)y\).
- Write the area of this inscribed rectangle as a function of the angle \(\theta\) shown in the diagram and then show that \(A = r^{2}\sin(2\theta)\).
- Use the formula from part (a) to determine the angle \(\theta\) that produces the largest value of \(A\) and determine the dimensions of this inscribed rectangle with the largest possible area.
Exercise \(\PageIndex{28}\)
Derive the Triple Angle Identity
\[\sin(3A) = -4\sin^{3}(A) + 2\sin(A)\]
for the sine with the following steps.
- Write \(3A\) as \(2A + A\) and apply the Sine Sum Identity to write \(\sin(3A)\) in terms of \(\sin(2A)\) and \(\sin(2A)\),
- Use Double Angle Identity to write \(\sin(2A)\) in terms of \(\sin(A)\) and \(\cos(A)\) and to write \(\cos(2A)\) in terms of \(\sin(A)\).
- Use a Pythagorean Identity to write \(\cos^{2}(2A)\) in terms of \(\sin^{2}(A)\) and simplify.
Exercise \(\PageIndex{29}\)
Derive the Quadruple Angle Identity
\[\sin(4x) = 4\cos(x)[\sin(x) - 2\sin^{3}(x)]\] as follows.
- Write s\[\sin(4x) = \sin(2(2x))\] and use the Double Angle Identity for sine to rewrite this formula.
- Now use the Double Angle Identity for sine and one of the Double Angle Identities for cosine to rewrite the expression from part (a).
- Algebraically rewrite the expression from part(b) to obtain the desired formula for \(\sin(4x)\).
Exercise \(\PageIndex{30}\)
Write each of the following expressions as a sum of trigonometric function values. When possible, determine the exact value of the resulting expression.
- \[\sin(37.5^\circ)\cos(7.5^\circ)\]
- \[\sin(75^\circ)\sin(15^\circ)\]
- \[\cos(44^\circ)\cos(16^\circ)\]
- \[\cos(45^\circ)\cos(15^\circ)\]
- \[\cos(\dfrac{5\pi}{12})\sin(\dfrac{\pi}{12})\]
- \[\sin(\dfrac{3\pi}{4})\cos(\dfrac{\pi}{12})\]
- Answer
-
(a) \(\sin(37.5^\circ)\cos(7.5^\circ) = \dfrac{1}{2}[\sin(45^\circ) + \sin(30^\circ)] = \dfrac{\sqrt{2} + 1}{4}\)
(e) \(\cos(\dfrac{5\pi}{12})\sin(\dfrac{\pi}{12}) = \dfrac{1}{2}[\sin(\dfrac{\pi}{2}) - \sin(\dfrac{\pi}{3})] = \dfrac{1 - \sqrt{3}}{4}\)
Exercise \(\PageIndex{31}\)
Write each of the following expressions as a sum of trigonometric function values. When possible, determine the exact value of the resulting expression.
- \[\sin(50^\circ) + \sin(10^\circ)\]
- \[\sin(195^\circ) - \sin(105^\circ)\]
- \[\cos(195^\circ) - \cos(15^\circ)\]
- \[\cos(76^\circ) + \cos(14^\circ)\]
- \[\cos(\dfrac{7\pi}{12}) + \cos(\dfrac{\pi}{12})\]
- \[\sin(\dfrac{7\pi}{4}) - \sin(\dfrac{5\pi}{12})\]
- Answer
-
(a) \(\sin(50^\circ) + \sin(10^\circ) = 2\sin(30^\circ)\cos(20^\circ) = \cos(20^\circ)\)
(e) \(\cos(\dfrac{7\pi}{12}) + \cos(\dfrac{\pi}{12}) = 2\cos(\dfrac{\pi}{3})\cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\)
Exercise \(\PageIndex{32}\)
Find all solutions to the given equation. Use a graphing utility to graph each side of the given equation to check your solutions.
- \[\sin(2x) + \sin(x) = 0\]
- \[\sin(x)\cos(x) = \dfrac{1}{4}\]
- \[\cos(2x) + \cos(x) = 0\]
- Answer
-
(a)\[\sin(2x) + \sin(x) = 0\]
\[2\sin(\dfrac{3x}{2})\cos(\dfrac{x}{2}) = 0\]
So \[\sin(\dfrac{3x}{2}) = 0\] or \[\cos(\dfrac{x}{2}) = 0\]. This gives \[x = k\pi\] or \[x = \dfrac{2\pi}{3} + k(2\pi)\] or \[x = \dfrac{4\pi}{3} + k(2\pi)\], where \(k\) is an integer.

