Home
Bookshelves
Precalculus & Trigonometry
Trigonometry (Sundstrom & Schlicker)
6: Some Geometric Facts about Triangles and Parallelograms

6: Some Geometric Facts about Triangles and Parallelograms

Last updated
Save as PDF

Page ID: 7130

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

This appendix contains some formulas and results from geometry that are important in the study of trigonometry.

Circles

For a circle with radius $r$:

Circumference: $C = 2\pi r$
Area: $A = \pi r^{2}$

$circles.png$

Triangles

The sum of the measures of the three angles of a triangle is $180^\circ$.
A triangle in which each angle has a measure of less that $90^\circ$ is called an acute triangle.
A triangle that has an angle whose measure is greater than $90^\circ$ is called an obtuse triangle.
A triangle that contains an angle whose measure is $90^\circ$ is called a right triangle. The side of a right triangle that is opposite the right angle is called the hypotenuse, and the other two sides are called the legs.
An isosceles triangle is a triangle in which two sides of the triangle have equal length. In this case, the two angles across from the two sides of equal length have equal measure.
An equilateral triangle is a triangle in which all three sides have the same length. Each angle of an equilateral triangle has a measure of $60^\circ$.

Right Triangles

The sum of the measures of the two acute angles of a right triangle is $90^\circ$. In the diagram on the right, $\alpha + \beta = 90^\circ$.
The Pythagorean Theorem. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In the diagram on the right, $c^{2} = a^{2} + b^{2}$

$right triangles.png$

Special Right Triangles

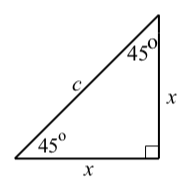
A right triangle in which both acute angles are $\textbf{45}^\circ$. For this type of right triangle, the lengths of the two legs are equal. So if $c$ is the length of the hypotenuse and $x$ is the length of each of the legs, then by the Pythagorean Theorem, $c^{2} = x^{2} + x^{2}$. Solving this equation for $x$, we obtain

\[2x^{2} = c^{2}\]
\[x^{2} = \dfrac{c^{2}}{2}\]
\[x = \sqrt{\dfrac{c^{2}}{2}}\]
\[x = \dfrac{x}{\sqrt{2}} = \dfrac{c\sqrt{2}}{2}\]

$SRT.png$

A right triangle with acute angles of $\textbf{30}^\circ$ and $\textbf{60}^\circ$.

We start with an equilateral triangle with sides of length $c$. By drawing an angle bisector at one of the vertices, we create two congruent right triangles with acute angles of $30^\circ$ and $60^\circ$.

$2.png$

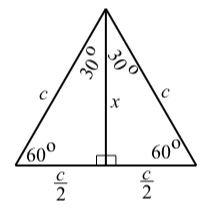
This means that the third side of each of these right triangles will have a length of $\dfrac{c}{2}$. If the length of the altitude is $x$, then using the Pythagorean Theorem, we obtain

\[c^{2} = x^{2} + (\dfrac{c}{2})^{2}\]
\[x^{2} = c^{2} - \dfrac{c^{2}}{4}\]
\[x^{2} = \dfrac{3c^{2}}{4}\]
\[x = \sqrt{\dfrac{3c^{2}}{4}} = \dfrac{c\sqrt{3}}{2}\]

Similar Triangles

Two triangles are similar if the three angles of one triangle are equal in measure to the three angles of the other triangle. The following diagram shows similar triangles $\triangle{ABC}$ and $\triangle{DEF}$. We write $\triangle{ABC} \sim \triangle{DEF}$.

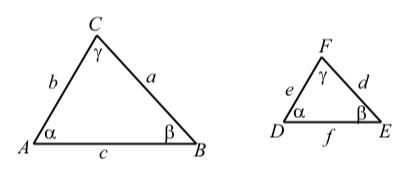
$ST.png$

The sides of similar triangles do not have to have the same length but they will be proportional. Using the notation in the diagram, this means that

\[\dfrac{a}{d} = \dfrac{b}{e} = \dfrac{c}{f}\]

Parallelograms

We use some properties of parallelograms in the study of vectors in Section 3.5. A parallelogram is a quadrilateral with two pairs of parallel sides. We will use the diagram on the right to describe some properties of parallelograms.

$P.png$

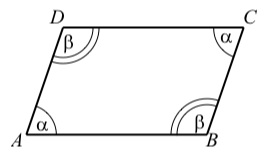
Opposite sides are equal in length. In the diagram, this means that \[AB = DC \space \text{and} \space AD = BC\]
As shown in the diagram, opposite angles are equal. That is, \[\angle{DAB} = \angle{BCD} \space \text{and} \space \angle{ABC} = \angle{CDA}\]
The sum of two adjacent angles is $180^\circ$. In the diagram, this means that \[\alpha + \beta = 180^\circ\]

Search

Text Color

Text Size

Margin Size

Font Type