5.E: Complex Numbers and Polar Coordinates (Exercises)

Exercise \(\PageIndex{1}\)

Write each of the following as a complex number in standard form.

1. \[(4 + i) + (3 - 3i)\]
2. \[5(2 - i) + i(3 - 2i)\]
3. \[(4 + 2i)(5 - 3i)\]
4. \[(2 + 3i)(1 + i) + (4 - 3i)\]

Answer

1. \((4 + i) + (3 - 3i) = 7 - 2i\)
2. \(5(2 - i) + i(3 -2i) = 12 - 2i\)
3. \((4 + 2i)(5 - 3i) = 26 - 2i\)
4. \((2 + 3i)(1 + i) + (4 - 3i) = 3 + 2i\)

Exercise \(\PageIndex{2}\)

Use the quadratic formula to write the two solutions of each of the following quadratic equations in standard form.

1. \[x^{2} - 3x + 5 = 0\]
2. \[2x^{2} = x - 7\]

Answer

(a) \(x = \dfrac{3}{2} + \dfrac{\sqrt{11}}{2}i, x = \dfrac{3}{2} - \dfrac{\sqrt{11}}{2}i\).

Exercise \(\PageIndex{3}\)

For each of the following pairs of complex numbers \(w\) and \(z\), determine the sum \(w + z\) and illustrate the sum with a diagram.

1. \[w = 3 + 2i, z = 5 - 4i.\]
2. \[w = 4i, z = -3 + 2i.\]
3. \[w = 5, z = -7 + 2i.\]
4. \[w = 6 - 3i, z = -1 + 7i.\]

Answer

1. \(w + z = 8 - 2i\)
2. \(w + z = -3 + 6i\)

Exercise \(\PageIndex{4}\)

For each of the following complex numbers \(z\), determine \(\bar{z}\), \(|z|\), and \(z\bar{z}\).

1. \[z = 5 + 2i\]
2. \[z = 3i\]
3. \[z = 3 - 4i\]
4. \[z = 7 + i\]

Answer

1. \(\bar{z} = 5 + 2i, |z| = \sqrt{29}, z\bar{z} = 29\)
2. \(\bar{z} = -3i, |z| = 3, z\bar{z} = 9\)

Exercise \(\PageIndex{5}\)

Write each of the following quotients in standard form.

1. \[\dfrac{5 + i}{3 + 2i}\]
2. \[\dfrac{3 + 3i}{i}\]
3. \[\dfrac{i}{2 - i}\]
4. \[\dfrac{4 + 2i}{1 - i}\]

Answer

1. \(\dfrac{5 + i}{3 + 2i} = \dfrac{17}{13} - \dfrac{7}{13}i\)
2. \(\dfrac{3 + 3i}{i} = 3 - 3i\)

Exercise \(\PageIndex{6}\)

1. We know that \(i^{1} = i\) and \(i^{2} = -1\). We can then see that \[i^{3} = i^{2}\cdot i = (-1)i = -i.\]
2. Show that \(i^{4} = 1\).
3. Now determine \(i^{5}, i^{6}, i^{7}\), and \(i^{8}\). Note: Each power of \(i\) will equal \(1, -1, i\), or \(-i\).
4. Notice that \(12 = 4\cdot 3 + 1\). We will use this to determine \(i^{13}\). \[i^{13} = i^{4\cdot 3 + 1} = i^{4\cdot 3}i^{1} = (i^{4})^{3}\cdot i\] So what is \(i^{13}\)?
5. Using \(39 = 4\cdot 9 + 3\), determine \(i^{39}\).
6. Determine \(i^{54}\).

Exercise \(\PageIndex{7}\)

1. Write the complex number \(i(2 + 2i)\) in standard form. Plot the complex numbers \(2 + 2i\) and \(i(2 + 2i)\) in the complex plane. What appears to be the angle between these two complex numbers?
2. Repeat part (a) for the complex numbers \(2 - 3i\) and \(i(2 - 3i)\).
3. Repeat part (a) for the complex numbers \(3i\) and \(i(3i)\).
4. Describe what happens when the complex number \(a + bi\) is multiplied by the complex number \(i\).

To make sense of solutions of quadratic equations that are not real, we introduce complex numbers. Although complex numbers arise naturally when solving quadratic equations, their introduction into mathematics came about from the problem of solving cubic equations.

Exercise \(\PageIndex{8}\)

Determine the polar (trigonometric) form of each of the following complex numbers.

1. \[3 +3i\]
2. \[3 -3i\]
3. \[-3 +3i\]
4. \[5i\]
5. \[4\sqrt{3} + 4i\]
6. \[-4\sqrt{3} - 4i\]

Answer

1. \(3 + 3i = \sqrt{18}(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4}))\)
2. \(4\sqrt{3} + 4i = 8(\cos(\dfrac{\pi}{6}) + i\sin(\dfrac{\pi}{6}))\)

Exercise \(\PageIndex{9}\)

In each of the following a complex number \(z\) is given. In each case, determine real numbers \(a\) and \(b\) so that \(z = a + bi\). If it is not possible to determine exact values for \(a\) and \(b\), determine the values of \(a\) and \(b\) correct to four decimal places.

1. \[z = 5(\cos(\dfrac{\pi}{2}) + i\sin(\dfrac{\pi}{2}))\]
2. \[z = 2.5(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4}))\]
3. \[z = 2.5(\cos(\dfrac{3\pi}{4}) + i\sin(\dfrac{3\pi}{4}))\]
4. \[z = 3(\cos(\dfrac{7\pi}{6}) + i\sin(\dfrac{7\pi}{6}))\]
5. \[z = 8(\cos(\dfrac{7\pi}{10}) + i\sin(\dfrac{7\pi}{10}))\]

Answer

1. \(5\cos(\dfrac{\pi}{2}) + i\sin(\dfrac{\pi}{2}) = 5i\)
2. \(2.5(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4})) = 1.25\sqrt{2} + 1.25\sqrt{2}i\)

Exercise \(\PageIndex{10}\)

For each of the following, write the product \(wz\) in polar (trigonometric form). When it is possible, write the product in form \(a + bi\), where \(a\) and \(b\) are real numbers and do not involve a trigonometric function.

1. \[w = 5(\cos(\dfrac{\pi}{12}) + i\sin(\dfrac{\pi}{12})), z = 2(\cos(\dfrac{5\pi}{12}) + i\sin(\dfrac{5\pi}{12}))\]
2. \[w = 2.3(\cos(\dfrac{\pi}{3}) + i\sin(\dfrac{\pi}{3})), z = 2(\cos(\dfrac{5\pi}{4}) + i\sin(\dfrac{5\pi}{4}))\]
3. \[w = 2(\cos(\dfrac{7\pi}{10}) + i\sin(\dfrac{7\pi}{10})), z = 2(\cos(\dfrac{2\pi}{5}) + i\sin(\dfrac{2\pi}{5}))\]
4. \[w = (\cos(24^\circ) + i\sin(24^\circ)), z = 2(\cos(33^\circ) + i\sin(33^\circ))\]
5. \[w = 2(\cos(72^\circ) + i\sin(72^\circ)), z = 2(\cos(78^\circ) + i\sin(78^\circ))\]

Answer

1. \(wz = 10(\cos(\dfrac{6\pi}{12}) + i\sin(\dfrac{6\pi}{12})) = 10i\)
2. \(wz = 6.9(\cos(\dfrac{19\pi}{12}) + i\sin(\dfrac{19\pi}{12}))\)

Exercise \(\PageIndex{11}\)

For the complex numbers in Exercise \(\PageIndex{10}\), write the quotient \(\dfrac{w}{z}\) in polar (trigonometric form). When it is possible, write the quotient in form \(a + bi\), where \(a\) and \(b\) are real numbers and do not involve a trigonometric function.Add text here. For the automatic number to work, you need to add the "AutoNum" template (preferably at the end) to the page.

Answer

(a) \(\dfrac{w}{z} = \dfrac{5}{2}(\cos(\dfrac{-4\pi}{12}) + i\sin(\dfrac{-4\pi}{12})) = \dfrac{5}{4} - \dfrac{5\sqrt{3}}{4}i\)

(b) \(\dfrac{w}{z} = \dfrac{23}{30}(\cos(\dfrac{-11\pi}{12}) + i\sin(\dfrac{-11\pi}{12}))\)

Exercise \(\PageIndex{12}\)

1. Write the complex number \(i\) in polar form.
2. Let \(z = r(\cos(\theta) + i\sin(\theta))\). Determine the product \(i\cdot z\) in polar form. Use this to explain why the complex number \(i\cdot z\) and \(z\) will be perpendicular when both are plotted in the complex plane.

Multiplication of complex numbers is more complicated than addition of complex numbers. To better understand the product of complex numbers, we first investigate the trigonometric (or polar) form of a complex number. This trigonometric form connects algebra to trigonometry and will be useful for quickly and easily finding powers and roots of complex numbers.

Exercise \(\PageIndex{13}\)

Use DeMoivre’s Theorem to determine each of the following powers of a complex number. Write the answer in the form \(a + bi\), where \(a\) and \(b\) are real numbers and do not involve the use of a trigonometric function.

1. \[(2 + 2i)^{6}\]
2. \[(\sqrt{3} + i)^{8}\]
3. \[(\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i)^{3}\]
4. \[2(\cos(\dfrac{\pi}{15}) + i\sin(\dfrac{\pi}{15}))^{10}\]
5. \[(1 + i\sqrt{3})^{-4}\]
6. \[(-3 + 3i)^{-3}\]

Answer

(a) \((2 + 2i)^{6} = [\sqrt{8}(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4}))]^{6} = 512i\)

(b) \((\sqrt{3} + i)^{8} = [2(\cos(\dfrac{\pi}{6}) + i\sin(\dfrac{\pi}{6}))]^{8} = -128 - 128\sqrt{3}i\)

Exercise \(\PageIndex{14}\)

In each of the following, determine the indicated roots of the given complex number. When it is possible, write the roots in the form a C bi , where a andb are real numbers and do not involve the use of a trigonometric function. Otherwise, leave the roots in polar form.

1. The two square roots of \(16i\).
2. The two square roots of \(2 + 2i\sqrt{3}\).
3. The three cube roots of \(5(\cos(\dfrac{3\pi}{4}) + i\sin(\dfrac{3\pi}{4}))\).
4. The five fifth roots of unity.
5. The four fourth roots of \((\dfrac{1}{2} - \dfrac{\sqrt{3}}{2}i)\).
6. The three cube roots of \(1 + \sqrt{3}i\).

Answer

(a) Write \(16i = 16(\cos(\dfrac{\pi}{2}) + i\sin(\dfrac{\pi}{2}))\). The two square roots of \(16i\) are \[4(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4})) = 2\sqrt{2} + 2i\sqrt{2}\]

\[4(\cos(\dfrac{5\pi}{4}) + i\sin(\dfrac{5\pi}{4})) = -2\sqrt{2} - 2i\sqrt{2}\]

(c) The three cube roots of \(5(\cos(\dfrac{3\pi}{4}) + i\sin(\dfrac{3\pi}{4}))\) are

\[\sqrt[3]{5}(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4})) = \sqrt[3]{5}(\dfrac{\sqrt{2}}{2} + \dfrac{\sqrt{2}}{2}i)\]
\[\sqrt[3]{5}(\cos(\dfrac{11\pi}{12}) + i\sin(\dfrac{11\pi}{12}))\]
\[\sqrt[3]{5}(\cos(\dfrac{19\pi}{12}) + i\sin(\dfrac{19\pi}{12}))\]

The trigonometric form of a complex number provides a relatively quick and easy way to compute products of complex numbers. As a consequence, we will be able to quickly calculate powers of complex numbers, and even roots of complex numbers.

Exercise \(\PageIndex{15}\)

Plot the following points with the specified polar coordinates.

Figure \(\PageIndex{1}\)

\[(7, \dfrac{\pi}{6})\] \[(3, \dfrac{3\pi}{4})\] \[(2, \dfrac{-\pi}{3})\]

\[(3, \dfrac{7\pi}{4})\] \[(5, \dfrac{-\pi}{4})\] \[(4, \dfrac{11\pi}{4})\]

\[(6, \dfrac{11\pi}{6})\] \[(-3, \dfrac{2\pi}{3})\] \[(-5, \dfrac{5\pi}{6})\]

Answer

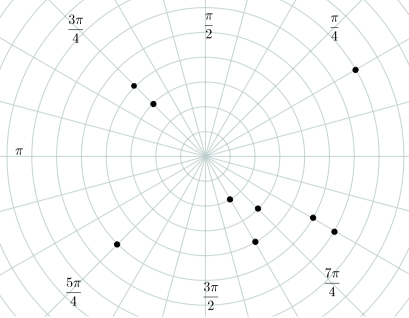
Figure \(\PageIndex{2}\)

Exercise \(\PageIndex{16}\)

For each of the following points in polar coordinates, determine three different representations in polar coordinates for the point. Use a positive value for the radial distance \(r\) for two of the representations and a negative value for the radial distance \(r\) for the other representation.

1. \[(5, 30^\circ)\]
2. \[(4, 100^\circ)\]
3. \[(-2, 50^\circ)\]
4. \[(7, -60^\circ)\]

Answer

(a) Some correct answers are: \((5, 390^\circ)\), \((5, -330^\circ)\), and \((-5, 210^\circ)\).

(b) Some correct answers are: \((4, 460^\circ)\), \((4, -260^\circ)\), and \((-4, 280^\circ)\).

Exercise \(\PageIndex{17}\)

For each of the following points in polar coordinates, determine three different representations in polar coordinates for the point. Use a positive value for the radial distance \(r\) for two of the representations and a negative value for the radial distance \(r\) for the other representation. Note: The angles are measured in radians.

1. \[(5, \dfrac{\pi}{6})\]
2. \[(4, \dfrac{5\pi}{9})\]
3. \[(-2, \dfrac{5\pi}{18})\]
4. \[(7, -\dfrac{\pi}{3})\]

Answer

1. Some correct answers are: \((5, \dfrac{13\pi}{6})\), \((5, -\dfrac{11\pi}{6})\), and \((-5, \dfrac{7\pi}{6})\).
2. Some correct answers are: \((4, \dfrac{23\pi}{9})\), \((4, -\dfrac{13\pi}{9})\), and \((-4, \dfrac{14\pi}{9})\).

Exercise \(\PageIndex{18}\)

Determine rectangular coordinates for each of the following points in polar coordinates:

1. \[(10, \dfrac{2\pi}{3})\]
2. \[(8, \dfrac{7\pi}{6})\]
3. \[(-5, \dfrac{5\pi}{4})\]
4. \[(10, -\dfrac{2\pi}{3})\]
5. \[(3, \dfrac{5\pi}{3})\]
6. \[(6, -\dfrac{\pi}{6})\]

Answer

1. \((-5, 5\sqrt{3})\)

3. \((\dfrac{5\sqrt{2}}{2}, \dfrac{5\sqrt{2}}{2})\)

Exercise \(\PageIndex{19}\)

Determine polar coordinates for each of the following points in rectangular coordinates. Use a positive radial distance \(r\) and a polar angle with \(0 \leq \theta < 2\pi\). When necessary, use an inverse trigonometric function and round the angle (in radians) to the nearest thousandth.

1. \[(\dfrac{-5\sqrt{3}}{2}, \dfrac{5}{2})\]
2. \[(3, 5)\]
3. \[(\sqrt{2}, -\sqrt{2})\]
4. \[(-3, -4)\]

Answer

1. \((5, \dfrac{5\pi}{6})\)

2. \((\sqrt{34}, \tan^{-1}(\dfrac{5}{3})) \approx (\sqrt{34}, 1.030)\)

Exercise \(\PageIndex{20}\)

Convert each of the following polar equations into a rectangular equation. If possible, write the rectangular equation with \(y\) as a function of \(x\).

1. \[r = 5\]
2. \[\theta = \dfrac{\pi}{3}\]
3. \[r = 8\cos(\theta)\]
4. \[r = 1 - \sin(\theta)\]
5. \[r^{2}\sin(2\theta) = 1\]
6. \[r = 1 - 2\cos(\theta)\]
7. \[r = \dfrac{3}{\sin(\theta) + 4\cos(\theta)}\]

Answer

1. \(x^{2} + y^{2} = 25\)

2. \(y = \dfrac{\sqrt{3}}{3}x\)

4. \(x^{2} + y^{2} = \sqrt{x^{2} + y^{2}} - y\)

Exercise \(\PageIndex{21}\)

Convert each of the following rectangular equations into a polar equation. If possible, write the polar equation with \(r\) as a function of \(\theta\).

1. \[x^{2} + y^{2} = 36\]
2. \[y = 4\]
3. \[x = 7\]
4. \[x^{2} - 6x + y^{2} = 0\]
5. \[x + y = 4\]
6. \[y = x^{2}\]

Answer

2. \(r\sin(\theta) = 4\) or \(r = \dfrac{4}{\sin(\theta)}\)

5. \(r\cos(\theta) + r\sin(\theta) = 4\) or \(r = \dfrac{4}{\cos(\theta) + \sin(\theta)}\)

Exercise \(\PageIndex{8}\)

Let a be a positive real number.

Convert the polar equation \(r = 2a\sin(\theta)\) to rectangular and then explain why the graph of this equation is a circle. What is the radius of the circle and what is the center of the circle in rectangular coordinates?

Convert the polar equation \(r = 2a\cos(\theta)\) to rectangular and then explain why the graph of this equation is a circle. What is the radius of the circle and what is the center of the circle in rectangular coordinates?

In our study of trigonometry so far, whenever we graphed an equation or located a point in the plane, we have used rectangular (or Cartesian) coordinates. The use of this type of coordinate system revolutionized mathematics since it provided the first systematic link between geometry and algebra. Even though the rectangular coordinate system is very important, there are other methods of locating points in the plane. We will study one such system in this section.