1.6: Other Trigonometric Functions
- Page ID
- 7102
Learning Objectives
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts mo- tivated by these questions and be able to write precise, coherent answers to these questions.
- How is the tangent function defined? What is the domain of the tangent function?
- What are the reciprocal functions and how are they defined? What are the domains of each of the reciprocal functions?
We defined the cosine and sine functions as the coordinates of the terminal points of arcs on the unit circle. As we will see later, the sine and cosine give relations for certain sides and angles of right triangles. It will be useful to be able to relate different sides and angles in right triangles, and we need other circular functions to do that. We obtain these other circular functions – tangent, cotangent, secant, and cosecant – by combining the cosine and sine together in various ways.
Beginning Activity
Using radian measure:
- For what values of \(t\) is \(\cos(t) = 0\)?
- For what values of \(t\) is \(\sin(t) = 0\)?
- In what quadrants is \(\cos(t) > 0\)? In what quadrants is \(\sin(t) > 0\)?
- In what quadrants is \(\cos(t) < 0\)? In what quadrants is \(\sin(t) < 0\)?
The Tangent Function
Next to the cosine and sine, the most useful circular function is the tangent.
The word tangent was introduced by Thomas Fincke (1561-1656) in his Flenspurgensis Geometriae rotundi libri XIIII where he used the word tangens in Latin. From Earliest Known Uses of Some of the Words of Mathematics at http://jeff560.tripod.com/mathword.html.
Definition: tangent function
The tangent function is the quotient of the sine function divided by the cosine function. So the tangent of a real number \(t\) is defined to be \(\dfrac{\sin(t)}{\cos(t)}\) for those values \(t\) for which \(\cos(t) \neq 0\). The common abbreviation for the tangent of \(t\) is
\[\tan(t) = \dfrac{\sin(t)}{\cos(t)}.\]
In this definition, we need the restriction that \(\cos(t) \neq 0\) to make sure the quotient is defined. Since \(\cos(t) \neq 0\) whenever \(t = \dfrac{\pi}{2} + k\pi\) for some integer \(k\), we see that \(\tan(t)\) is defined when \(t \neq \dfrac{\pi}{2} + k\pi\) for all integers \(k\). So the domain of the tangent function is the set of all real numbers \(t\) for which \(t \neq \dfrac{\pi}{2} + k\pi\) for every integer \(k\). Notice that although the domain of the sine and cosine functions is all real numbers, this is not true for the tangent function.
When we worked with the unit circle definitions of cosine and sine, we often used the following diagram to indicate signs of \(\cos(t)\) and \(\sin(t)\) when the terminal point of the arc t is in a given quadrant.
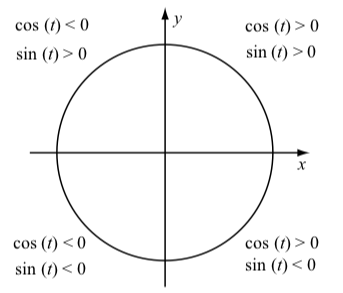
Exercise \(\PageIndex{1}\)
Considering \(t\) to be an arc on the unit circle, for the terminal point of \(t\):
- In which quadrants is \(\tan(t)\) positive?
- In which quadrants is \(\tan(t)\) negative?
- For what values of \(t\) is \(tan(t) = 0\)?
- Complete Table 1.4, which gives the values of cosine, sine, and tangent at the common reference arcs in Quadrant I.
| \(t\) | \(\cos(t)\) | \(\sin(t)\) | \(\tan(t)\) |
|---|---|---|---|
| 0 | 0 | ||
| \(\dfrac{\pi}{6}\) | \(\dfrac{1}{2}\) | ||
| \(\dfrac{\pi}{4}\) | \(\dfrac{\sqrt{2}}{2}\) | ||
| \(\dfrac{\pi}{4}\) | \(\dfrac{\sqrt{3}}{2}\) | ||
| \(\dfrac{\pi}{2}\) | 1 |
- Answer
-
- Since \(\tan(t) = \dfrac{\sin(t)}{\cos(t)}\), \(\tan(t)\) positive when both \(\sin(t)\) and \(\cos(t)\) have the same sign. So \(\tan(t) > 0\) in the first and third quadrants.
- We see that \(\tan(t)\) negative when \(\sin(t)\) and \(\cos(t)\) have opposite signs. So \(\tan(t) < 0\) in the second and fourth quadrants.
- \(\tan(t)\) will be zero when \(\sin(t) = 0\) and \(\cos(t) \neq 0\). So \(\tan(t) = 0\) when the terminal point of \(t\) is on the \(x\)-axis. That is, \(\tan(t) = 0\) when \(t = k\pi\) for some integer \(k\).
- Following is a completed version of Table 1.4.
\(t\) \(\cos(t)\) \(\sin(t)\) \(\tan(t)\) \(0\) \(1\) \(0\) \(0\) \(\dfrac{\pi}{6}\) \(\dfrac{\sqrt{3}}{2}\) \(\dfrac{1}{2}\) \(\dfrac{1}{\sqrt{3}}\) \(\dfrac{\pi}{4}\) \(\dfrac{\sqrt{2}}{2}\) \(\dfrac{\sqrt{2}}{2}\) \(1\) \(\dfrac{\pi}{4}\) \(\dfrac{1}{2}\) \(\dfrac{\sqrt{3}}{2}\) \(\sqrt{3}\) \(\dfrac{\pi}{2}\) \(0\) \(1\) undefined
Just as with the cosine and sine, if we know the values of the tangent function at the reference arcs, we can find its values at any arc related to a reference arc. For example, the reference arc for the arc \(t = \dfrac{5\pi}{3}\) is \(\dfrac{\pi}{3}\).
\[\tan(\dfrac{5\pi}{3}) = \dfrac{\sin(\dfrac{5\pi}{3})}{\cos(\dfrac{5\pi}{3})} = -\dfrac{\sin(\dfrac{\pi}{3})}{\cos(\dfrac{\pi}{3})} = \dfrac{-\dfrac{\sqrt{3}}{2}}{\dfrac{1}{2}} = -\sqrt{3}\]
So we can shorten this process by just using the fact that \(\tan(\dfrac{\pi}{3}) = \sqrt{3}\) and that \(\tan(\dfrac{5\pi}{3}) < 0\) since the terminal point of the arc \(\dfrac{5\pi}{3}\) is in the fourth quadrant. \[\tan(\dfrac{5\pi}{3}) = -\tan(\dfrac{\pi}{3}) = -\sqrt{3}\]
Exercise \(\PageIndex{2}\)
- Determine the exact values of \(t = \dfrac{5\pi}{4}\) and \(t = \dfrac{5\pi}{6}\).
- Determine the exact values of \(\cos(t)\) and \(\tan(t)\) if it is known that \(\sin(t) = \dfrac{1}{3}\) and \(\tan(t) < 0\).
- Answer
-
1. \[\tan(\dfrac{5\pi}{4}) = \tan(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\] \[\tan(\dfrac{6\pi}{6}) = -\tan(\dfrac{\pi}{6}) = -\dfrac{1}{\sqrt{3}}\]
2. We first use the Pythagorean Identity. \[\cos^{2}(t) + \sin^{2}(t) = 1\] \[\cos^{2}(t) + (\dfrac{1}{3})^{2} = 1\] \[\cos^{2}(t) = \dfrac{8}{9}\]
Since \(\sin(t) > 0\) and \(\tan(t) < 0\), we conclude that the terminal point of \(t\) must be in the second quadrant, and hence, \(\cos(t) < 0\). Therefore,
\[\cos(t) = -\dfrac{\sqrt{8}}{3}\] \[\tan(t) = \dfrac{\dfrac{1}{3}}{-\dfrac{\sqrt{8}}{3}} = -\dfrac{1}{\sqrt{8}}\]
The Reciprocal Functions
The remaining circular or trigonometric functions are reciprocals of the cosine, sine, and tangent functions. Since these functions are reciprocals, their domains will be all real numbers for which the denominator is not equal to zero. The first we will introduce is the secant function.
Definition: secant function
The secant function is the reciprocal of the cosine function. So the secant of a real number \(t\) is defined to be \(\dfrac{1}{\cos(t)}\) for those values \(t\) where \(\cos(t) \neq 0\). The common abbreviation for the secant of \(t\) is \[\sec(t) = \dfrac{1}{\cos(t)}.\]
Since the tangent function and the secant function use \(\cos(t)\) in a denominator, they have the same domain. So the domain of the secant function is the set of all real numbers \(t\) for which \(t \neq \dfrac{\pi}{2} + k\pi\) for every integer \(k\).
The term secant was introduced by was by Thomas Fincke (1561-1656) in his Thomae Finkii Flenspurgensis Geometriae rotundi libri XIIII, Basileae: Per Sebastianum Henricpetri, 1583. Vieta (1593) did not approve of the term secant, believing it could be confused with the geometry term. He used Transsinuosa instead. From Earliest Known Uses of Some of the Words of Mathematics at http://jeff560.tripod.com/mathword.html.
Next up is the cosecant function.
Definition: cosecant function
The cosecant function is the reciprocal of the secant function. So the cosecant of a real number \(t\) is defined to be \(\dfrac{1}{\sin(t)}\) for those values t where \(\sin(t) \neq 0\). The common abbreviation for the secant of \(t\) is \[\csc(t) = \dfrac{1}{\sin(t)}.\]
Since \(\sin(t) = 0\) whenever \(t = k\pi\) for some integer \(k\), we see that the domain of the cosecant function is the set of all real numbers t for which \(t \neq k\pi\) for every integer \(k\).
Finally, we have the cotangent function.
Definition: cotangent function
The cotangent function is the reciprocal of the secant function. So the cotangent of a real number \(t\) is defined to be \(\dfrac{1}{\tan(t)}\) for those values t where \(\tan(t) \neq 0\). The common abbreviation for the secant of \(t\) is \[\cot(t) = \dfrac{1}{\tan(t)}.\]
Since \(\tan(t) = 0\) whenever \(t = k\pi\) for some integer \(k\), we see that the domain of the cotangent function is the set of all real numbers \(t\) for which \(t \neq k\pi\) for every integer \(k\).
Georg Joachim von Lauchen Rheticus appears to be the first to use the term cosecant (as cosecans in Latin) in his Opus Palatinum de triangulis. From Earliest Known Uses of Some of the Words of Mathematics at http://jeff560.tripod.com/mathword.html.
The word cotangent was introduced by Edmund Gunter in Canon Triangulorum (Table of Artificial Sines and Tangents) where he used the term cotangens in Latin. From Earliest Known Uses of Some of the Words of Mathematics at http://jeff560.tripod.com/mathword.html.
A Note about Calculators
When it is not possible to determine exact values of a trigonometric function, we use a calculator to determine approximate values. However, please keep in mind that many calculators only have keys for the sine, cosine, and tangent functions. With these calculators, we must use the definitions of cosecant, secant, and cotangent to determine approximate values for these functions.
Exercise \(\PageIndex{3}\)
When possible, find the exact value of each of the following functional values. When this is not possible, use a calculator to find a decimal approximation to four decimal places.
- \(\sec(\dfrac{7\pi}{4})\)
- \(\csc(\dfrac{-\pi}{4})\)
- \(\tan(\dfrac{7\pi}{8})\)
- \(\cot(\dfrac{4\pi}{3})\)
- \(\csc(5)\)
- Answer
-
- \[\sec(\dfrac{7\pi}{4}) = \dfrac{1}{\cos(\dfrac{7\pi}{4})} = \dfrac{1}{\cos(\dfrac{\pi}{4})} = \dfrac{2}{\sqrt{2}} = \sqrt{2}\]
- \[\csc(-\dfrac{\pi}{4}) = \dfrac{1}{\sin(-\dfrac{\pi}{4})} = \dfrac{1}{\sin(-\dfrac{\pi}{4})} = -\dfrac{2}{\sqrt{2}} = -\sqrt{2}\]
- \[\tan(\dfrac{7\pi}{8}) \approx -0.4142\]
- \[\cot(\dfrac{4\pi}{3}) = \cot(\dfrac{\pi}{3}) = \dfrac{1}{\tan(\dfrac{\pi}{3})} = \dfrac{2}{\sqrt{3}}\]
- \[\csc(5) = \dfrac{1}{\sin(5)} \approx -1.0428\]
Exercise \(\PageIndex{4}\)
- If \(\cos(t) = \dfrac{1}{3}\) and \(\sin(t) < 0\), determine the exact values of \(\sin(t)\), \(\tan(t)\), \(\csc(t)\), and \(\cot(t)\).
- If \(\sin(t) = \dfrac{-7}{10}\) and \(\tan(t) > 0\), determine the exact values of \(\cos(t)\) and \(\cot(t)\).
- What is another way to write \((\tan(t))(\cos(t))\)?
- Answer
-
1. If \(\cos(x) = \dfrac{1}{3}\) and \(\sin(x) < 0\), we use the Pythagorean Identity to determine that \(\sin(x) = -\dfrac{\sqrt{8}}{3}\). We can then determine that
\[\tan(x) = -\sqrt{8}\] \[\csc(x) = -\dfrac{3}{\sqrt{8}}\] \[\cot(t) = -\dfrac{1}{\sqrt{8}}\]
2. If \(\sin(x) = -0.7\) and \(\tan(x) > 0\), we use the Pythagorean Identity to obtain \[\cos^{2}(x) + (-0.7)^{2} = 1\] \[\cos^{2}(x) = 0.51\]
Since we are also given that \(\tan(x) > 0\), we know that the terminal point ofx is in the third quadrant. Therefore, \(\cos(x) < 0\) and \(\cos(x) = -\sqrt{0.51}\). Hence,
\[\tan(x) = \dfrac{-0.7}{-\sqrt{0.51}}\] \[\cot(x) = \dfrac{\sqrt{0.51}}{0.7}\]
3. We can use the definition of \(\tan(x)\) to obtain \[(\tan(x))(\cos(x)) = \dfrac{\sin(x)}{\cos(x)}\cdot \cos(x) = \sin(x)\]
So \(\tan(x)\cos(x) = \sin(x)\), but it should be noted that this equation is only valid for those values of \(x\) for which \(\tan(x)\) is defined. That is, this equation is only valid if \(x\) is not an integer multiple of \(\pi\).
Summary
In this section, we studied the following important concepts and ideas:
- The tangent function is the quotient of the sine function divided by the cosine function. So is the quotient of the sine function divided by the cosine function. That is, \(\tan(t) = \dfrac{sin(t)}{\cos(t)}\) for those values \(t\) for which \(\cos(t) \neq 0\). The domain of the tangent function is the set of all real numbers \(t\) for which \(t \neq \dfrac{\pi}{2} + k\pi\) for every integer \(k\).
- The reciprocal functions are the secant, cosecant, and tangent functions.
|
Reciprocal Function |
Domain |
|---|---|
| \(\sec(t) = \dfrac{1}{\cos(t)}\) | The set of all real numbers \(t\) for which \(t \neq \dfrac{\pi}{2} + k\pi\) for every integer \(k\) |
| \(\csc(t) = \dfrac{1}{\sin(t)}\) | The set of all real numbers t for which \(t \neq k\pi\) for every integer \(k\). |
| \(\cot(t) = \dfrac{1}{\tan(t)}\) | The set of all real numbers t for which \(t \neq k\pi\) for every integer \(k\). |


