1.1: Exponent Properties and More!
- Page ID
- 83107
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Folks remember, above all else, properties of math! Properties allow us to transform an expression or an equation into an equivalent form. We often need to use properties to move through a problem’s solution. This section introduces several properties. For all the properties in this section, the variables \(a\), \(b\), and \(c\) represent real numbers. Here are a few properties, followed by examples for their use:
\[a + b = b+ a\]
The order of addition does not matter.
\[ab = ba\]
The order of multiplication does not matter.
Evaluate \(40 + −6 + 12 + 6 + −40\)
Solution
The commutative property of addition allows us to add in any order.
\(\begin{array} &&40 + −40 + 6 + −6 + 12 &\text{Rearrange the order to group opposites.} \\ &= 0 + 0 + 12 &\text{Opposites sum to zero.} \\ &= 12 \end{array}\)
Why is \(20\%\) of \(45\) the same as \(45\%\) of \(20\)?
Solution
Let’s verify the two expressions are equivalent:
\(\begin{array} &&0.20 \cdot 45 = 9 &\text{\(20\%\) of \(45\) is \(9\).} \\ &0.45 \cdot 20 = 9 &\text{\(45\%\) of \(20\) is \(9\).} \end{array}\)
The commutative property of multiplication tells us why it’s true.
\(\begin{array} &&20 \cdot 0.01 \cdot 45 = 45 \cdot 0.01 \cdot 20 &\text{The order of multiplication is just rearranged.} \end{array}\)
The commutative property, as demonstrated, shows why the equivalency holds.
Caution! The order of division and subtraction matters. Therefore, the commutative property only applies to multiplication and addition, NOT to division nor subtraction.
\[a(b+c) = ab + ac\]
The distributive property can be visualized as a rectangular area which is the sum of two smaller rectangular areas:
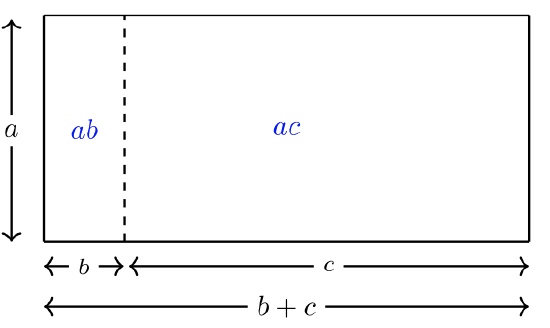
Simplify \(6(2x + 7)\)
Solution
\(\begin{array}&&6(2x + 7) = 6(2x) + 6(7) \\ &= 12x + 42 \end{array}\)
\[x^a \cdot x^b = x^{a+b}\]
There are many power properties. Understanding why each property holds will help you decide whether to add or multiply exponents. Here’s why the Product Property holds:
\( \underbrace{\underbrace{x \cdot x \cdot x \cdot x \cdot ... \cdot x}_{\text{\(a\) number of \(x\)'s}} \cdot \underbrace{x \cdot x \cdot x \cdot x \cdot ... \cdot x}_{\text{\(b\) number of \(x\)'s}}}_{\text{\(a+b\) number of \(x\)}} = x^a \cdot x^b = x^{a+b} \)
\[(x^a)^b) = x^{ab}\]
Again, understand why the property holds will help you master the rule:
\(\underbrace{x^a \cdot x^a \cdot x^a \cdot x^a \cdot ... \cdot x^a}_{\text{\(b\) number of \(x^a\)'s}} = \underbrace{x^{a+a+a+...+a}}_{\text{Product of Powers Property}} = \underbrace{\underbrace{x^{ba}}_{a+a+a+...+a \;= \;ba} }_{\text{\(b\) number of \(a\)'s} } = x^{ab}\)
Simplify each of the following expressions.
- \(5y^8 \cdot y^4 \cdot y\)
- \(9(d^2)^3\)
- \(6u \cdot 3u^4 + (u^3)^2\)
Solution
- Product of Powers Property
\(\begin{array} &&5y^8 \cdot y^4 \cdot y \\ &= 5 \cdot y^{8+4+1} \\ &= 5y^{13} \end{array}\)
- Power of a Power
\(\begin{array} &&9(d^2)^3 \\ &= 9d^{2 \cdot 3} \\ &= 9d^6 \end{array}\)
- Both properties are used:
\(\begin{array} &&6u \cdot 3u^4 + (u^3)^2 \\ &= 6 \cdot 3 \cdot u^{1+4} \cdot u^{3 \cdot 2} \\ &= 18u^5 + u^6 \end{array}\)
The sum of powers can be simplified only if the powers are identical in base and exponent. For example, \(x^3 + 7x^3 = (1 + 7)x^3 = 8x^3\). Simplify by combining like terms. Otherwise, the powers cannot be simplified. See solution to Example 4c.
\[(xy)^{a} = x^a \cdot y^a\]
Each factor inside the parentheses is raised to the power indicated.
\[b^{-n} = \left( \dfrac{1}{b} \right)^{n} = \dfrac{1}{b^n} \]
Create the reciprocal of base \(b\), then raise \(b\) to the positive power, \(n\).
Think of the negative exponent as if it were flagging the power, letting you know that it is in the wrong place.
Simplify each of the following expressions.
- \((3n)^4\)
- \(2(−4x^3y^2z)^2\)
- \((−2u^{−3}w^5 )^{−4}\)
Solution
- \(\begin{array} &&(3n)^4 \\ &=3^n \cdot 4^n \\ &=81n^4 \end{array}\)
- \(\begin{array} &&2(−4x^3y^2z)^2 \\ &=2(−4)^2 (x^3)^2(y^2)^2 (z)^2 \\ &=2 \cdot 16 \cdot x^{3 \cdot 2} \cdot y^{2 \cdot 2} \cdot z^2 \\ &= 32x^6y^4z^2 \end{array}\)
- \(\begin{array} &&(−2u^{−3}w^5 )^{−4} \\ &= (-2)^{-4} \cdot (u^{-3})^{-4} \cdot (w^5)^{-4} \\ &= \dfrac{1}{-2^4} \cdot u^{(-3)(-4)} \cdot w^{(5)(-4)} \\ &=\dfrac{u^{12}}{16w^{20}} \end{array}\)
\[\left( \dfrac{a}{b} \right)^{n} = \dfrac{a^n}{b^n}\]
The power is applied to both the numerator and the denominator.
Simplify \(\left( \dfrac{5a^{-1}b^2}{2c^6} \right)^{-2}\)
Solution
Let’s approach the solution like pealing an onion, beginning with the outer layer:
\(\begin{array} &&=\left(\dfrac{2c^6}{5a^{-1}b^2}\right)^{2} &\text{The reciprocal of the fraction is taken. The power becomes positive.} \\ &= \left(\dfrac{2ac^6}{5b^2}\right)^{2} &\text{The negative exponent flags the power. \(\dfrac{1}{a^{-1}} = \dfrac{1}{\frac{1}{a}} = 1 \cdot a = a\)} \\ &= \left(\dfrac{(2ac^6)^2}{(5b^2)^2}\right) &\text{The Power of a Quotient Property is applied.} \\ &=\dfrac{2^2 \cdot a^2 \cdot (c^6)^2}{5^2 \cdot (b^2)^2} &\text{The Power of a Product Property is applied.} \\ &=\dfrac{4a^2c^{12}}{25b^4} &\text{The Power of a Power Property is applied. All is simplified.} \end{array}\)
\[\dfrac{x^a}{x^b} = x^{a-b} \]
The exponents are subtracted is due to the cancellation of common factors. For example, \(\dfrac{x^5}{x^3} = \dfrac{\cancel{x} \cdot \cancel{x} \cdot \cancel{x} \cdot x \cdot x}{\cancel{x} \cdot \cancel{x} \cdot \cancel{x}} = \dfrac{x \cdot x}{1} =x^2 = x^{5-3} \). Similarly, \(\dfrac{x^3}{x^5} = \dfrac{\cancel{x} \cdot \cancel{x} \cdot \cancel{x}}{\cancel{x} \cdot \cancel{x} \cdot \cancel{x} \cdot x \cdot x} = \dfrac{1}{x \cdot x} =x^{-2} = x^{3-5} \)
Simplify \(\left( \dfrac{4p^3q}{2p^2q^5} \right)^2\)
Solution
\(\begin{array} &&=\left( \dfrac{4}{2} \cdot p^{3-2} \cdot q^{1-5} \right)^2 &\text{The Quotient of Powers Property is applied.}\\ &=(2pq^{-4})^2 \text{The exponents are simplified.} \\ &=2^2 \cdot p^2 \cdot (q^{-4})^2 &\text{The Power of a Product Property is applied.} \\ &=4p^2q^{(-4)(2)} &\text{The Power of a Power Property is applied.} \\ &=4p^2q^{-8} &\text{The negative exponent flags the power \(q^8\).} \\ &= \dfrac{4p^2}{q^8} &\text{The power \(q^8\) belongs in the denominator. All is simplified.} \end{array}\)
Try It! (Exercises)
1. Name the property the equation demonstrates.
- \((5 \cdot 7)^2 = 5^2 \cdot 7^2\)
- \(5(−20 + 2) = 5(−20) + 5(2)\)
- \(7(x + 1) = (x + 1) \cdot 7\)
- \(6^{12} \cdot 6^3 = 6^{15}\)
- \(8 + (−9) = −9 + 8\)
- \(4^{30} = (4^5)^6\)
2. Evaluate the following sum. Rearrange the terms so a calculator isn’t necessary.
- \(12 + 84 + (−1) + (−84) + (−12) + 10\)
- \((−1.9) + (−5.8) + 13.2 + 1.9 + 5.8 + (−1.2)\)
For #3-11, use the distributive property to simplify.
- \(10(7x + 9)\)
- \(2y^2 (8 + 2y)\)
- \(−7p(4p^4 + 1)\)
- \(3b[b^3 + (−2)]\)
- \(4u(5u^2 + 9u − 1)\)
- \(n^3m(2n^4m − 9nm^2 + 8)\)
- \(\dfrac{1}{2} \left( \dfrac{3}{4} − z^2 \right)\)
- \(\dfrac{2}{5} q^2 (5q + 10)\)
- \(\dfrac{7}{8} t(2t^2 − 4t + 3)\)
12. The commutative property applies to addition and multiplication. The commutative property does NOT apply to subtraction nor to division. The symbol ≠ means “does not equal.” Show that the two sides of the inequality produce different results.
- \(6 − 2 ≠ 2 − 6\)
- \(10 ÷ 5 ≠ 5 ÷ 10\)
For #13-15, use power properties to simplify. Answers should contain positive exponents only.
- \((3n)^2 + (5n)(6n)\)
- \(( 5x^3 2y )^3\)
- \((−3a^5b^{−2}c)^4\)
16. Scientific Notation, coupled with rules for exponents, eases the computations with very large and very small numbers. Use power properties to evaluate each of the following. Leave your answer in scientific notation. Leave negative powers of \(10\) as is for the final answer.
- \((6.02 x 10^{24})(1.3 x 10^{15})\)
- \((3.14 x 10^{10})(2.65 x 10^{18})\)
- \((7.4 x 10^{−6} )(1.25 x 10^{−4} )\)
- \((3.8 x 10^{−16})(2.4 x 10^{−8} )\)
For #17-25, use power properties to simplify. Answers should contain positive exponents only. Use fractions, not decimals.
- \(\dfrac{12w^6}{4w}\)
- \(\dfrac{5u^2}{10u^3}\)
- \(\left( \dfrac{5}{4} \right)^{−1}\)
- \(\left( \dfrac{6t}{3} \right)^{−2}\)
- \(\left( \dfrac{4n^6}{2n} \right)^{−1}\)
- \(\left( \dfrac{7pq^5}{28p^3q} \right)^{2}\)
- \(\left( \dfrac{12x^{10}y^3}{24x^9y^8} \right)^{3}\)
- \(\left( \dfrac{9ab^{12}c^4}{27a^7bc^3} \right)^{−4}\)
- \(\left( \dfrac{6r^5 s^{−2}}{15r^{−1}s} \right)^{−3}\)
For #26-35, simplify using properties.
- \(2(3x + 10) + 5(2x − 1)\)
- \(4a^3 (a + 1) − 2a^2 (a^2 − a)\)
- \((8y^2 ) 2 − 3(7y^3 )(2y)\)
- \((4d)(9d^3)(2d^2) − (5d^3)^2\)
- \(\dfrac{1}{2} b^4 (6b − 2) − (3b^2 )^2\)
- \(\dfrac{3}{4} uv(8u − 4v) + \dfrac{3}{2} u \left(uv + \dfrac{2v}{u} \right)\)
- \(p^2q(4p + 3q) − (2pq)^2\)
- \(5mn^2 (m − n) − 4m^2 (n^2 − 1)\)
- \(10c^8 (2c^{−3} + c^{−4}) + c^{−2} (c^6 − 12c^7 )\)
- \(3n^7 (3n^{−2} )^{−1} + 2n^8 (n − 1) + (-n^{3} )^3\)