Skip to main content
Mathematics LibreTexts

1.2: FOIL Method and Special Products

  1. Last updated
  2. Save as PDF
  • Page ID
    83108

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    In this section, examples are given for multiplying a binomial (\(2\)-term polynomial) to another binomial. In some cases, the FOIL method yields predictable patterns. We call these “special products.” Recognizing special products will be useful when we turn to solving quadratic equations.

    Real numbers inform how and why rules work within algebraic expressions. For that reason, let’s examine how to multiply the real numbers: \(53 \times 27\).

    You might complete the problem using a traditional approach learned in grade school. This approach is shown below.

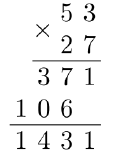
    clipboard_e55390c108993ead74561c60a31214d32.png

    Alternatively, we can use total rectangular area to find the product \(53 \times 27\). The area total area is the sum of four smaller rectangular areas.

    Step 1: Write both \(53\) and \(27\) as the sum of tens and ones:

    \(\begin{array}&&53 = 50 + 3\\ &27 = 20 + 7 \end{array}\)

    Step 2: Each side length of the larger rectangle is broken into the sum of tens and ones.

    Step 3: Find the area of each of the four smaller rectangles.

    Step 4: Sum the four areas to find the total area.

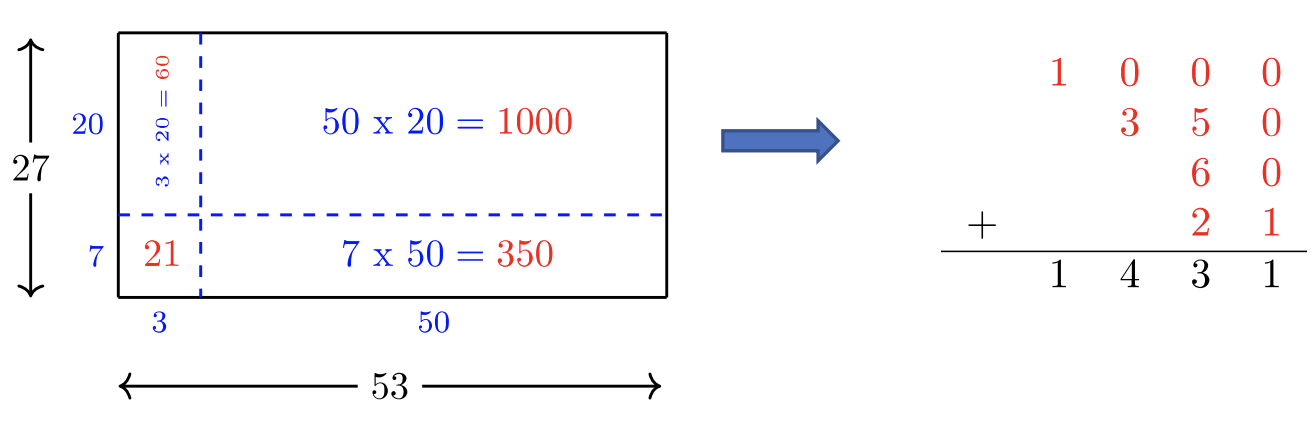
    clipboard_eb2dac278b5ef889b846be7a322fb80ba.png

    By either method, the correct answer is \(53 \times 27 = (50 + 3)(20 + 7) = 1431\).

    However, the rectangular area method informs us how binomials are correctly multiplied. We can follow a pattern of multiplication called FOIL: First Outer Inner Last.

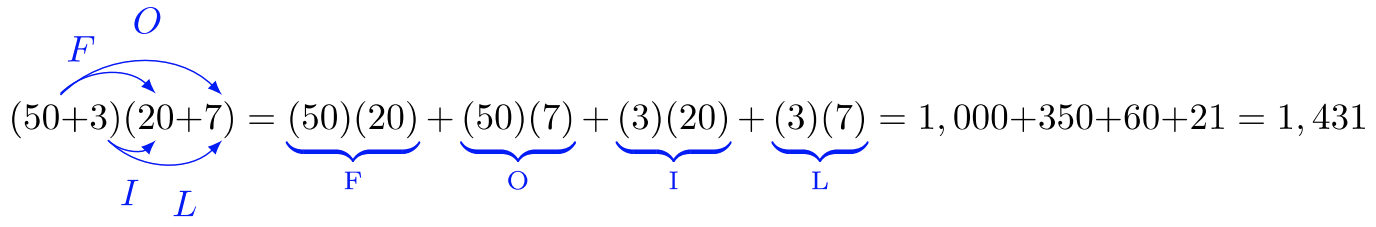
    clipboard_e583d6af916de22d5c96bd2d6c330edcd.png

    Binomials containing algebraic expressions will behave the same way real numbers behave. The FOIL method is required when variables stand in the place of real numbers.

    Example 1.2.1

    Multiply \((2x + 5)(3x + 2)\).

    Solution

    Use the FOIL method:

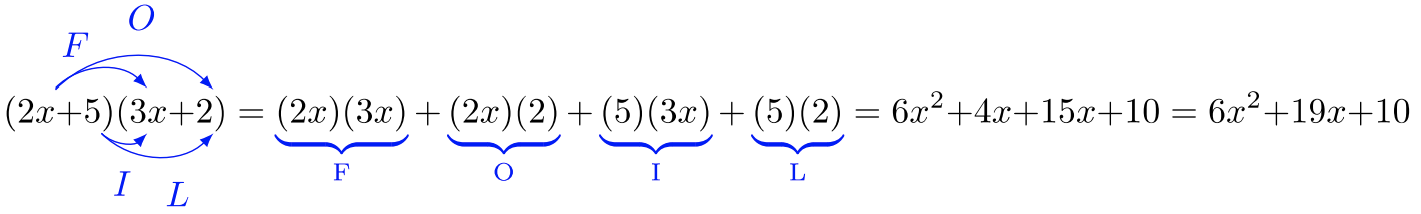
    clipboard_ed9513a55ff4b749682e9d63685df77dc.png

    Example 1.2.2

    Multiply \((2x − 5)(x − 4)\).

    Solution

    Use the FOIL method. Subtraction can be changed to addition, \((2x + (−5))(x + (−4))\), but it’s customary to allow subtraction to be perceived as a negative rather than writing it as such. In short, pay attention to your negative values and adjust the operation (add or subtract) accordingly.

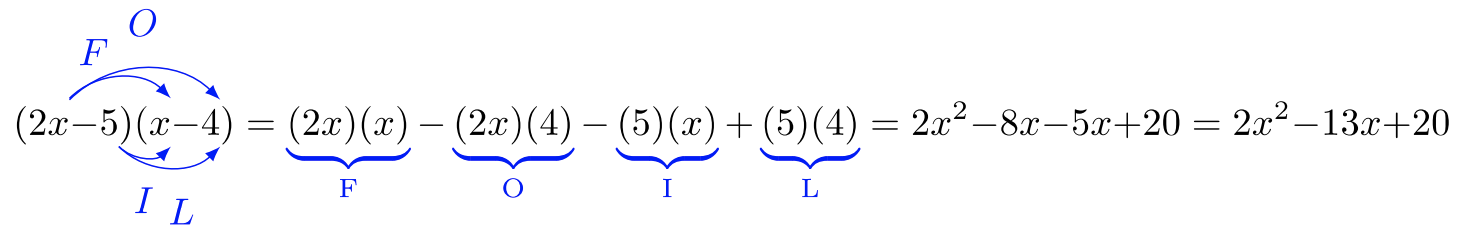
    clipboard_e97bab29a0f6ea4fecc5f6e375afc0008.png

    Special Products of Binomials

    The FOIL method can be reliably used to multiply all binomials. That is, you are not required to use the following special products if you wish to continue using FOIL. However, getting used to observing mathematical patterns and using patterns is a good math skill to hone.

    Case 1: Same terms, but one binomial is a sum, while the other binomial is a difference.

    Example 1.2.3

    Multiply \((3x + 7)(3x − 7)\)

    Solution

    By the FOIL method: \((3x + 7)(3x − 7) = 9x^2 − 21x + 21x − 49 = 9x^2 - 49\) The two middle terms cancel.

    Case 2: Same terms, and same operation: either both are plus, or both are minus.

    Example 1.2.4

    Multiply \((5x + 2)(5x + 2)\)

    Solution

    By the FOIL method: \((5x + 2)(5x + 2) = 25x^2 + 10x + 10x + 4 = 25x^2 + 20x+ 4\) The two middle terms are the same. Double up!

    Special Products of Binomials

    \[(A+B)(A-B) = A^2 - B^2\]

    The product is called a difference of squares.

    \[(A+B)^2 = (A+B)(A+B) = A^2 + 2AB + B^2 \\ (A-B)^2 = (A-B)(A-B) = A^2 - 2AB + B^2\]

    The product is called a perfect square trinomial.

    Example 1.2.5

    Multiply \((10x − 3)^2\).

    Solution

    Use the Special Product Formula: \((A-B)^2 = (A-B)(A-B) = A^2 - 2AB + B^2\)

    Determine the values \(A\) and \(B\). The formula will require these substitutions: \(A = 10x \text{ and } B = 3\)

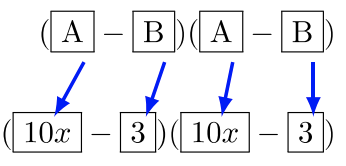
    clipboard_eb124014ae3b884dc0c0c04d49ddf6841.png

    \(\begin{array} &&A^2 - 2AB + B^2 &\text{Substitute \(A=10x\) and \(B=3\)} \\&=(10x)^2 - 2(10x)(3)+ 3^2 & \\&= 100x^2 - 60x + 9 & \end{array}\)

    Answer \((10x − 3)^2 = 100x^2 - 60x + 9\)

    Example 1.2.6

    Multiply \((6x − 11)(6x + 11)\)

    Solution

    Use the Special Product Formula: \((A-B)(A+B) = A^2 - B^2\)

    Determine the values \(A\) and \(B\). The formula will require these substitutions: \(A = 6x \text{ and } B = 11\)

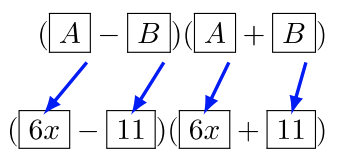
    clipboard_e1f0eac5dc643a5a102444812b1fe11c1.png

    \(\begin{array} &&A^2 - B^2 &\text{Substitute \(A=6x\) and \(B=11\)} \\&=(6x)^2 - 11^2 & \\&= 36x^2 - 121 & \end{array}\)

    Answer: \((6x − 11)(6x + 11) = 36x^2 - 121\)

    Example 1.2.7

    What property of multiplication is demonstrated in the following equation?

    \((6x − 11)(6x + 11) = (6x + 11)(6x − 11)\)

    Solution

    The quantities \((6x − 11)\) and \((6x + 11)\) stand in the place of real numbers \(a\) and \(b\). The order of multiplication does not yield different results. That is, for all real numbers \(a\) and \(b\), \(ab = ba\). The equation demonstrates the Commutative Property of Multiplication.

    Multiplying Polynomials of More Than 2 Terms

    Finally, let’s tackle multiplying polynomials of any number of terms, not just binomials. The FOIL method was developed using area of a rectangle. We’ll use the same method to develop a strategy for multiplying polynomials of more than \(2\) terms to each other.

    Example 1.2.8

    Multiply \((2x^2 − 4x + 5)(x^2 + 6x − 8)\)

    Solution

    The concept of a rectangle’s area will be our guide1.

    \(\underbrace{(2x^2 - 4x + 5)}_{\text{Length}} \;\underbrace{(x^2 + 6x - 8)}_{\text{Width}} = \text{ Total Area}\)

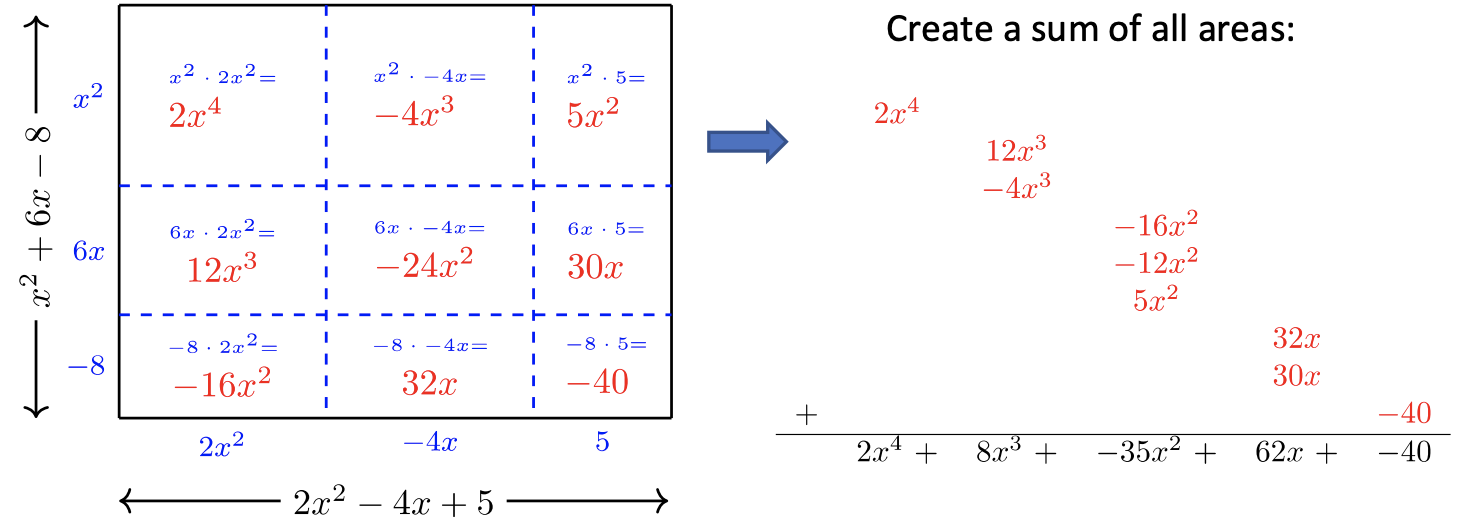
    clipboard_e286323f9c65834edbc15c7e41dc44dbb.png

    Answer: \((2x^2 − 4x + 5)(x^2 + 6x − 8) = 2x^4 + 8x^3 -35x^2 +62x -40\)

    Example 1.2.9

    Multiply \(2x(x^3 − 5)(x^2 − 7x + 10)\)

    Solution

    We have \(3\) quantities, \(2x\), \(x^3 − 5\), and \(x^2 − 7x + 10\). These quantities stand in the place of real numbers. If three real numbers were multiplied, for example: \(3 \cdot 4 \cdot 7\), how would you do it? Select any two numbers to multiply! \((3 \cdot 4)^7 = 12 \cdot 7 = 84\). Likewise, algebra follows the same rules.

    \(\begin{array} &&[2x(x^3 − 5)](x^2 − 7x + 10) &\text{Multiply two quantities together.} \\ &(2x^4 − 10x)(x^2 − 7x + 10) &\text{Use the distributive property to multiply.} \end{array}\)

    Create a table with the terms of each polynomial representing length and width of a rectangle:

    \(x^2\) \(-7x\) \(10\)
    \(2x^4\) \(2x^6\) \(-14x^5\) \(20x^4\)
    \(-10x\) \(-10x^3\) \(70x^2\) \(-100x\\)

    Answer \(2x(x^3 − 5)(x^2 − 7x + 10) = 2x^6 - 14x^5 +20x^4 -10x^3 +70x^2 -100x\)

    Try It! (Exercises)

    For #1-12, multiply using the FOIL method.

    1. \((x + 7)(x + 6)\)
    2. \((y + 5)(y + 3)\)
    3. \((2t + 9)(t + 1)\)
    4. \((n − 2)(n + 4)\)
    5. \((p + 8)(p− 11)\)
    6. \((3q − 1)(2q + 1)\)
    7. \((10 − m)(12 − m)\)
    8. \((15 − w)(2 + w)\)
    9. \((9 + u)(2 − u)\)
    10. \((5z + 12)(z − 1)\)
    11. \((3r + 7)(2r − 7)\)
    12. \((6n + 5)(6n − 4)\)

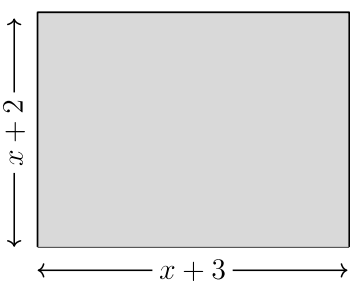
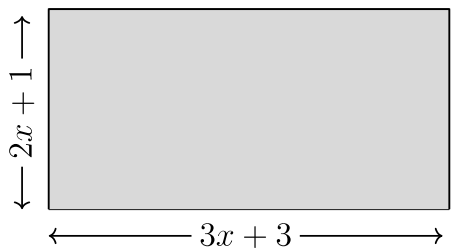
    For #13-14, find the polynomial that represents the area of each rectangle.

    13. clipboard_e82d14c7075079b25a78a177da5280272.png

    14. clipboard_efc41a433f360f90f66fb741bd99c1e4b.png

    For #15-23, use an appropriate Special Products Formula to multiply.

    1. \((y + 5)^2\)
    2. \((p − 3)(p + 3)\)
    3. \((t − 7)^2\)
    4. \((7q − 1)(7q + 1)\)
    5. \((4n + 9)^2\)
    6. \((8c + 6)(8c − 6)\)
    7. \((2u − 2)^2\)
    8. \((4 − z)^2\)
    9. \((5 − 3r)^2\)

    For #24-31, multiply the polynomials.

    1. \((x − 8)(x^2 − 3x + 1)\)
    2. \((2y + 3)(y^2 − 6y − 4)\)
    3. \((u^2 + 1)(u^2 + 2u − 5)\)
    4. \((4p^2 − p + 2)(p^2 + 2p − 3)\)
    5. \(2h(3h − 1)(6h + 1)\)
    6. \(5t(t − 4)(t^2 + 3t − 2)\)
    7. \((2n + 1)^3\)
    8. \(4b(b − 3)^2\)

    This page titled 1.2: FOIL Method and Special Products is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jennifer Freidenreich.