7.2: Reference Angles

Last updated
Save as PDF

Page ID: 83152

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The Special Right Triangles, $30˚$-$60˚$-$90˚$ and $45˚$-$45˚$-$90˚$, allow us to obtain exact values of the ordered pairs $(x, y)$ on a unit circle with standard angles $30˚$, $45˚$, or $60˚$.

If we use symmetry across the $y$-axis and the $x$-axis, we can populate the known ordered pairs from QI into Quadrants II, III, and IV. Use the figures below to follow how this is done. To keep the pictures simple, $30˚$ angles are marked, while $45˚$ and $60˚$ can be surmised by their larger magnitudes.

Figure 7.2.1 : QI → QII $(x, y) → (−x, y)$

Figure 7.2.2 : QII → QIII $(−x, y) → (−x, −y)$

Figure 7.2.3 : QII → QIII $(-x, −y) → (x, −y)$

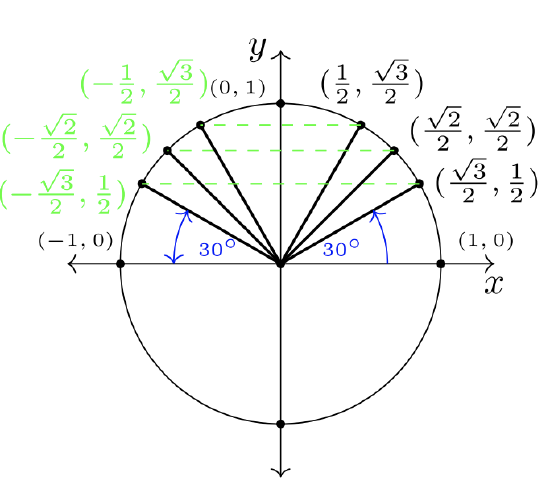
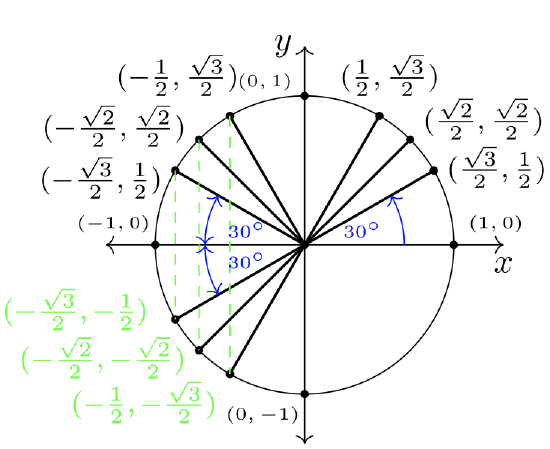
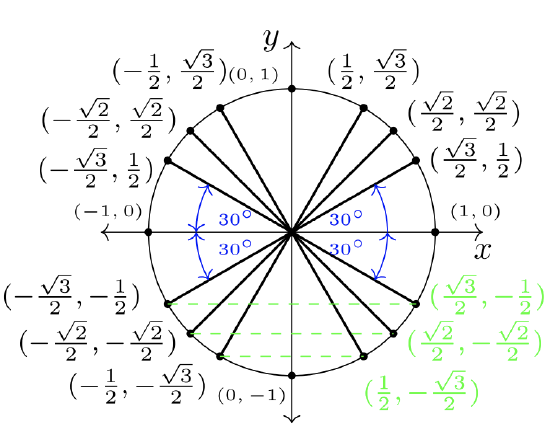
Notice the four $30˚$ angles create a bow-tie look in Figure $7.2.3$. These angles are called reference angles.

Definition: Reference Angle

Let $\theta$ be a standard angle. A reference angle, denoted $\hat{\theta}$, is the positive acute angle between the terminal side of $\theta$ and the $x$-axis.

The word reference is used because all angles can refer to QI. That is, memorization of ordered pairs is confined to QI of the unit circle. If a standard angle $\theta$ has a reference angle of $30˚$, $45˚$, or $60˚$, the unit circle’s ordered pair is duplicated, but the sign value of $x$ or $y$ may need adjustment, depending on the quadrant of the terminal side of $\theta$.

Example 7.2.1

The terminal side of a standard angle $\theta = 225˚$ intersects the unit circle. State the ordered pair of the intersection.

Solution

The unit circle has radius $r = 1$. Trigonometry weds algebra and geometry with visual sketches. We start with a sketch of the angle $\theta = 225˚$. All standard angles begin on the positive-side of the $x$-axis. In which quadrant is the terminal side of $\theta$? That is, where does this angle come to a stop?

Where is the terminal side of $\theta = 225˚$? Since $180˚ < 225˚ < 270˚$, the angle’s terminal side is in QIII.

The reference angle is computed by finding The difference between $225˚$ and $180˚$.

Note: The reference angle is never negative.

$|225˚ − 180˚| = |180˚ − 225˚| = \hat{\theta}$

$45˚ = \hat{\theta}$

In QIII, all ordered pairs $(x, y)$ are such that $x < 0$ and $y < 0$. Referring back to QI, using standard angle of $45˚$ on the unit circle, the ordered pair $\left( \dfrac{\sqrt{2}}{2} , \dfrac{\sqrt{2}}{2} \right)$ must be adjusted for negative $x$ and $y$ coordinates.

Answer The terminal side of $\theta = 225˚$ intersects the unit circle at $\left( −\dfrac{\sqrt{2}}{2} , −\dfrac{\sqrt{2}}{2} \right)$.

Tip: When a standard angle is greater than $90˚$, use markers $180˚$ or $360˚$ to calculate the reference angle. Drawing a picture before computing is always recommended!

QII: $90˚ < \theta < 180˚$
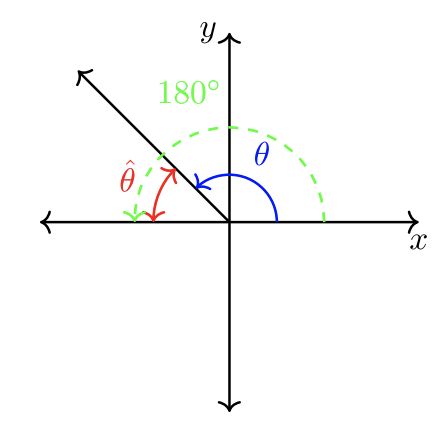
$|180˚ − \theta| = \textcolor{red}{\hat{\theta}}$

QIII: $180˚ < \theta < 270˚$
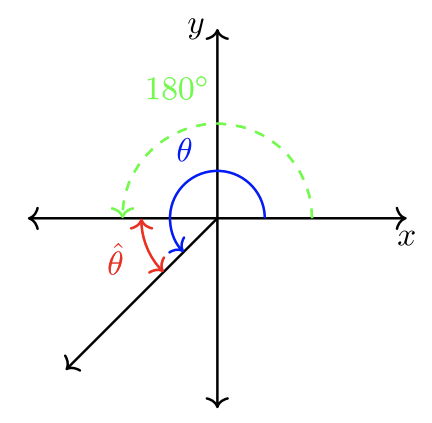
$|180˚ − \theta| = |\theta − 180˚| = \textcolor{red}{\hat{\theta}}$

QIV: If $270˚ < \theta < 360˚$
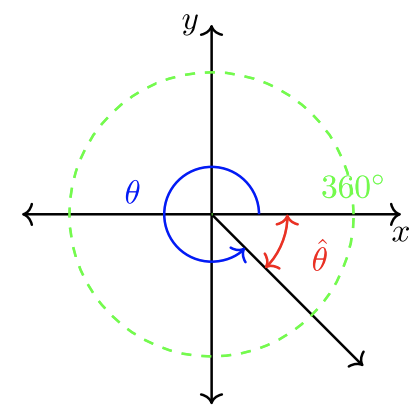
$|360˚ − \theta| = \textcolor{red}{\hat{\theta}}$

Example 7.2.2

The terminal side of a standard angle $\theta = −480˚$ intersects the unit circle. State the ordered pair of the intersection.

Solution

Negative angles rotate clockwise. Sketch $\theta$. Find a positive coterminal angle: $−480˚ + 360˚(2) = 240˚$ Then apply the tips above or analyze visually: $|180˚ − 240˚| = |−60˚| = 60˚ = \hat{\theta}$

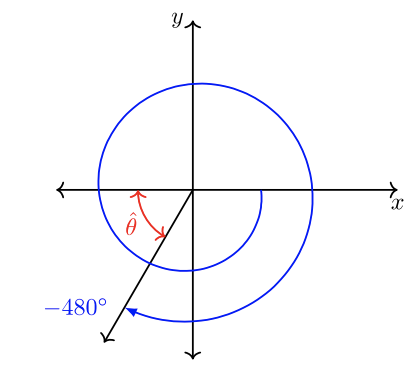
$clipboard_e2e05a1fabdfb42e49534221af0acffe0.png$

The ordered pair on the unit circle is $\left(−\dfrac{1}{2} , −\dfrac{\sqrt{3}}{2} \right)$.

Try It! (Exercises)

For #1-10, state the reference angle, $\hat{\theta}$, of the given standard angle.

$\theta = 210˚ $
$\theta = 350˚$
$\theta = 110˚$
$\theta = 240.5˚$
$\theta = 142.75˚$
$\theta = −315˚$
$\theta = −230˚$
$\theta = 500˚$
$\theta = 615˚$
$\theta = −835˚$

For #11-20, the terminal side of the given standard angle, $\theta$, intersects the unit circle at a point. State the ordered pair of the intersection.

$\theta = 135˚$
$\theta = 300˚$
$\theta = −240˚$
$\theta = −150˚$
$\theta = 420˚$
$\theta = 570˚$
$\theta = 840˚$
$\theta = −765˚$
$\theta = −930˚$
$\theta = 1560˚$

For #21-28, a standard angle’s rotation is described in words. You are given several hints about its rotation. Note: a full revolution is $360˚$ (counter-clockwise) or $-360˚$ (clockwise). Find the measure of the angle described.

An angle has a counter-clockwise rotation. The angle does not make a full revolution. The angle’s terminal side is in QIV. The reference angle $\hat{\theta} = 30˚$.
An angle has a counter-clockwise rotation. The angle does not make a full revolution. The angle’s terminal side is in QII. The reference angle $\hat{\theta} = 20˚$.
An angle has a clockwise rotation. The angle does not make a full revolution. The angle’s terminal side is in QIII. The reference angle $\hat{\theta} = 10˚$.
An angle has a clockwise rotation. The angle does not make a full revolution. The angle’s terminal side is in QII. The reference angle $\hat{\theta} = 72˚$.
An angle has a counter-clockwise rotation. The angle goes just beyond one full revolution. The angle’s terminal side is in QI. The reference angle $\hat{\theta} = 55˚$.
An angle has a counter-clockwise rotation. The angle goes beyond two full revolutions. The angle’s terminal side is in QII. The reference angle $\hat{\theta} = 24˚$.
An angle has a clockwise rotation. The angle goes beyond one full revolution. The angle’s terminal side is in QIII. The reference angle $\hat{\theta} = 18˚$.
An angle has a clockwise rotation. The angle goes beyond two full revolutions. The angle’s terminal side is in QIV. The reference angle $\hat{\theta} = 39˚$.