7.3: Radians
- Page ID
- 83154
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Angles can be measured in units of degrees or radians.
Radians are a unit of angular measure defined such that
\[2\pi \text{ radians } = 360˚\]
For the crafty at heart, an angle of \(1\) radian can be created with a circle (use any lid from a jar) and a piece of string.


Recall that the circumference of a circle (which is the perimeter of a circle) has a formula:
Circumference = \(C = 2 \pi r\) where \(r =\) radius of the circle
How many strings of length \(r\) are needed to wrap around the entire circle? We divide the circumference \(r\) ways: \(\dfrac{2 \pi r}{r} = 2 \pi ≈ 6\). About \(6\) strings of length \(r\), or exactly \(2 \pi\) strings.
An angle’s counter-clockwise rotation can be measured as a fraction of a full rotation.
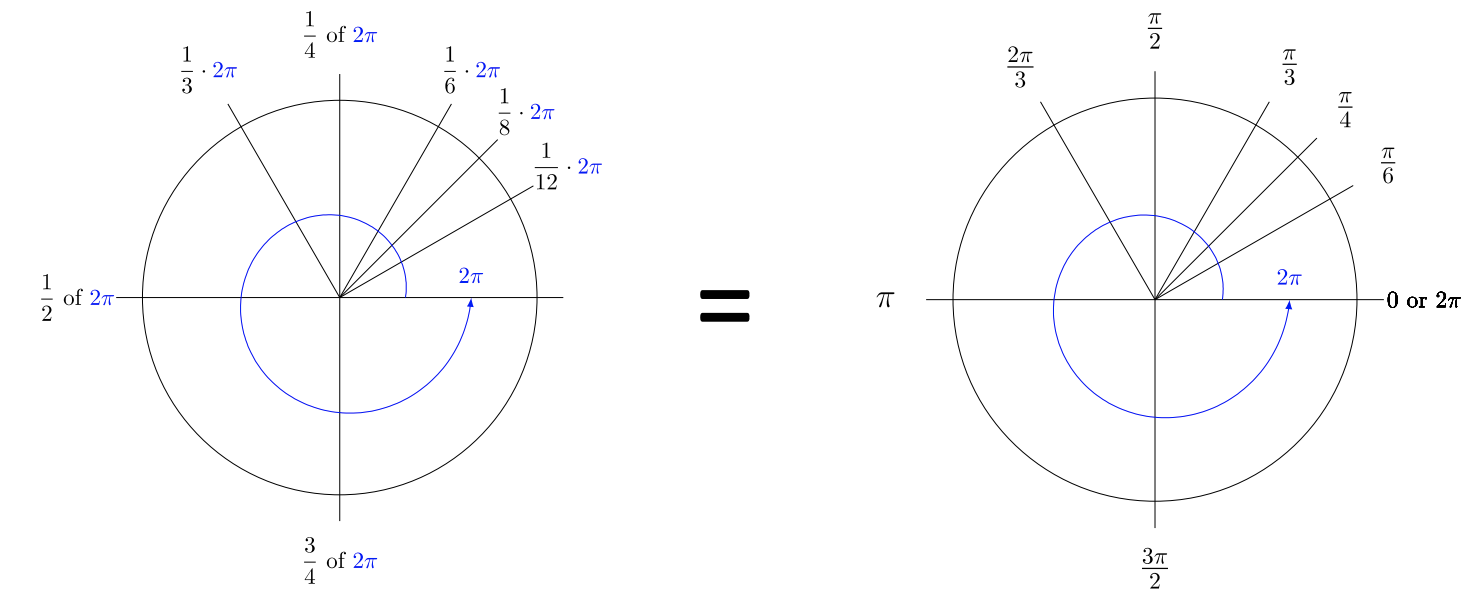
Once you get the hang of radians, your trigonometric calculations are quick and easy. Using radians for angles, rather than degrees, is the key to gain fluidity in trigonometry. They are simpler to use than degrees. Notice the shared denominators from one quadrant to the next. Also notice the denominator of an angle matches its own reference angle’s denominator.
\(30˚ = \dfrac{\pi}{6} \text{ radians } \;\;\;\;\;\;\;\;\;\;\;\;\; 45˚ = \dfrac{\pi}{4} \text{ radians } \;\;\;\;\;\;\;\;\;\;\;\;\; 60˚ = \dfrac{\pi}{3} \text{ radians }\)
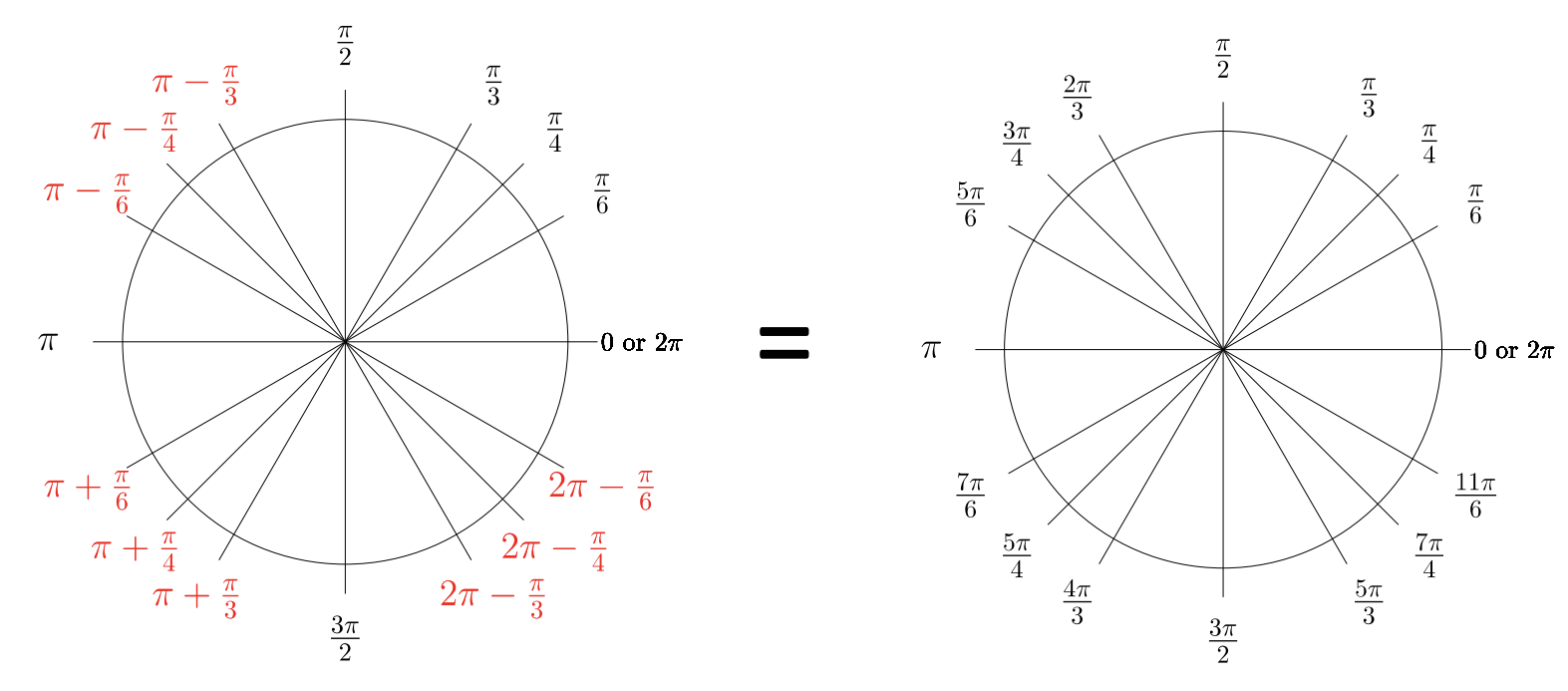
Reference angles refer to QI, where your memorization comes into play. Memorize only QI and the unit circle’s ordered pairs in that quadrant (see Section 7.2). Avoid memorizing too much! Use intuitive computations to rehearse math concepts. If a radian value is not one of the above values, nor coterminal to the ones shown, then you will need a calculator for trigonometric computations.
Give the reference angle \(\hat{\theta}\) (in radians) for the given standard angle \(\theta\). Then sketch both \(\theta\) and \(\hat{\theta}\).
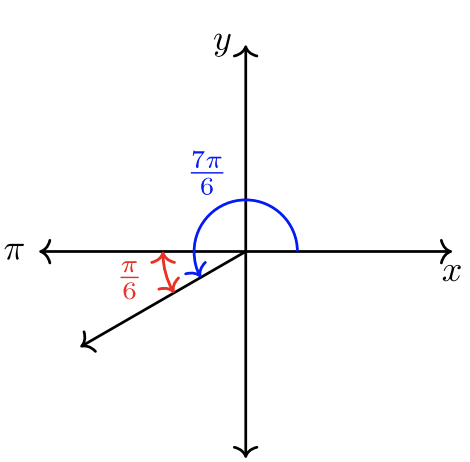
- \(\theta = \dfrac{7 \pi}{6}\)
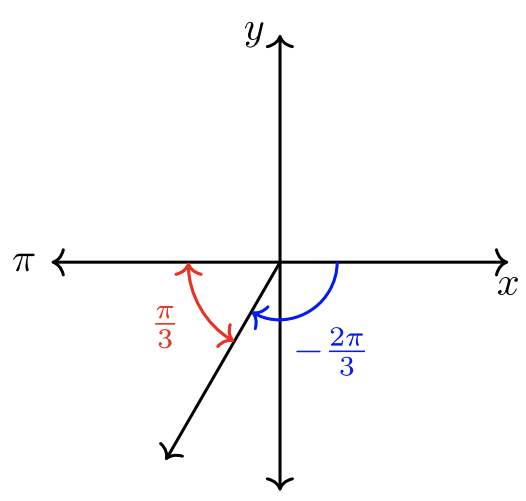
- \(\theta = − \dfrac{2 \pi}{3}\)
- \(\theta = \dfrac{11 \pi}{4}\)
- \(\theta = 6 \text{ radians}\)
Solution
- \(\theta = \dfrac{7 \pi}{6}\). Decide whether \(\dfrac{7 \pi}{6}\) is closer to \(\pi\) or \(2 \pi\).
Since \(\pi = \dfrac{6\pi}{6}\) and \(2\pi = \dfrac{12\pi}{6}\), it is clear that \(\dfrac{7\pi}{6} > \dfrac{6\pi}{6}\) and closer to \(\pi\).
The reference angle is \(\hat{\theta} = \dfrac{\pi}{6}\).
\(\dfrac{7\pi}{6} = \pi + \dfrac{\pi}{6}\).
The sketch is shown below.
- \(\theta = − \dfrac{2 \pi}{3}\). The angle rotates clockwise.
\(\left|− \dfrac{2\pi}{3} \right| = \dfrac{2\pi}{3}\) which terminates in QII.
The clockwise rotation of \(−\dfrac{2\pi}{3}\) terminates in QIII.
Both \(\dfrac{2\pi}{3}\) and \(−\dfrac{2\pi}{3}\) have the same reference angle.
\(\hat{\theta} = \dfrac{\pi}{3}\).
The sketch is shown below.
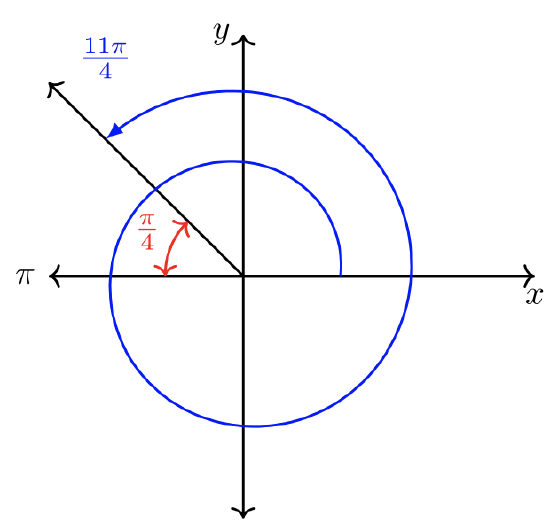
- \(\theta = \dfrac{11 \pi}{4}\). The denominator is \(4\).
Since \(\dfrac{8\pi}{4} = 2\pi\) and \(\dfrac{11\pi}{4} > \dfrac{8\pi}{4}\), this angle rotates beyond one full revolution. \(\pi\) is coterminal with \(3\pi\), \(5\pi\), \(7\pi\) … while \(2\pi\) is coterminal with \(4\pi\), \(6\pi\), \(8\pi\),...
Compare \(\dfrac{11\pi}{4}\) to \(3\pi = \dfrac{12\pi}{4}\). They are very close in value! \(\dfrac{11\pi}{4} < \dfrac{12\pi}{4}\) and \(\dfrac{11\pi}{4}\) therefore terminates In QII. The reference angle \(\hat{\theta} = \dfrac{\pi}{4}\).
The sketch of the angle is shown below.
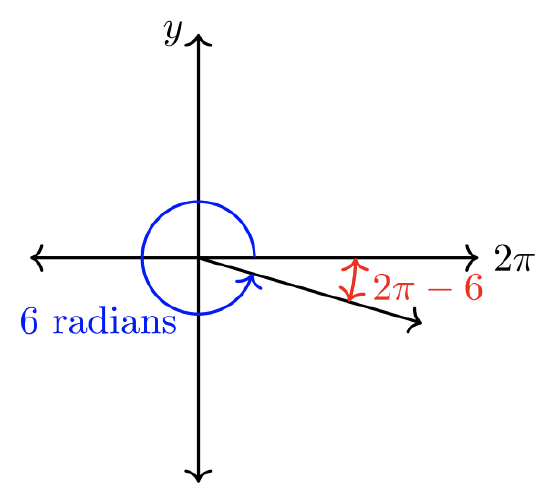
- \(\theta = 6 \text{ radians}\). Decide whether \(6\) radians is closer to \(\pi\) or \(2\pi\).
Since \(\pi ≈ 3.14\) and \(2\pi ≈ 6.28\), \(6\) radians is closer to \(2\pi\). \(6 < 2\pi\), therefore the angle terminates in QIV.
The reference angle \(\hat{\theta} = 2\pi − 6 ≈ 0.28\) radians.
The sketch of the angle is shown below.
The terminal side of a standard angle \(\theta = \dfrac{3\pi}{4}\) radians intersects the unit circle. State the ordered pair of the intersection.
Solution
Since \(\dfrac{3\pi}{4} = \dfrac{4\pi}{4} − \dfrac{\pi}{4}\), the angle \(\theta = \dfrac{3\pi}{4}\) terminates in QII with reference angle \(\hat{\theta} = \dfrac{\pi}{4}\).
The unit circle was introduced in Section 7.2 for degree-angles. The figure shown below includes radian-angles.
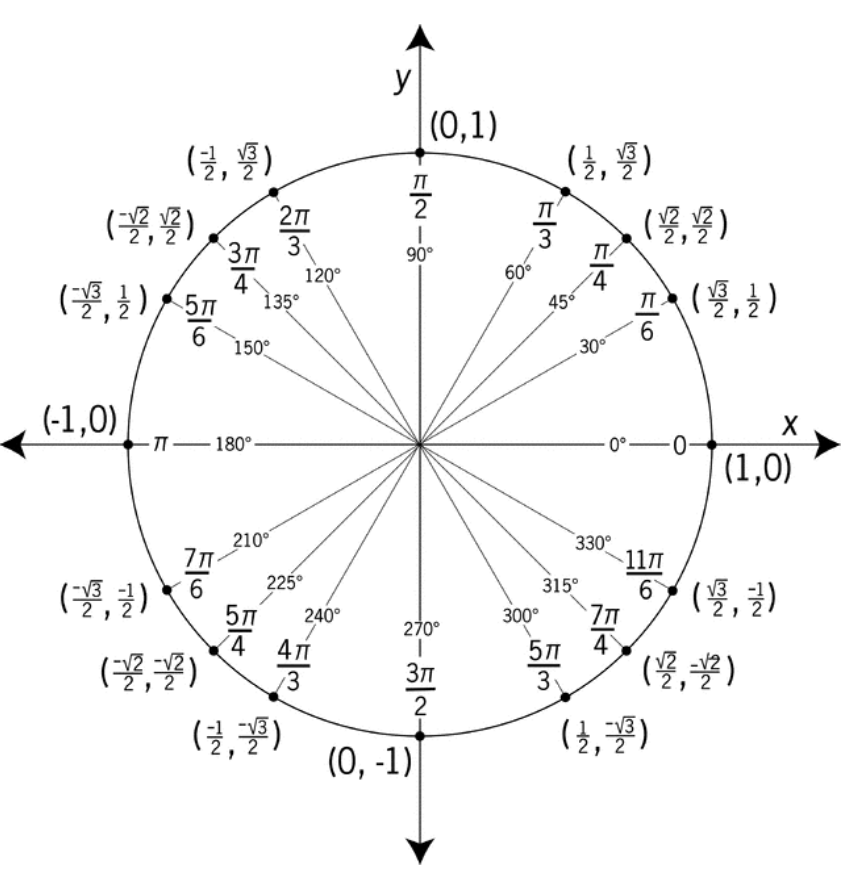
The ordered pair on the unit circle, intersecting the terminal side of \(\pi = \dfrac{3\pi}{4}\) is \(\left(−\dfrac{\sqrt{2}}{2} , \dfrac{\sqrt{2}}{2} \right)\).
The terminal side of a standard angle \(\theta = \dfrac{5\pi}{2}\) radians intersects the unit circle. State the ordered pair of the intersection.
Solution
Since \(\dfrac{5\pi}{2} = \dfrac{\pi}{2} + 2\pi\), the angles \(\dfrac{5\pi}{2}\) and \(\dfrac{\pi}{2}\) are coterminal angles. Coterminal angles land in the same spot, so the ordered pair will be the same. The ordered pair on the unit circle, intersecting the terminal side of \(\theta = \dfrac{5\pi}{2}\) is \((0, 1)\).
The terminal side of a standard angle \(\theta = 10\pi\) radians intersects the unit circle. State the ordered pair of the intersection.
Solution
Since \(10\pi = 2\pi(5)\), the angles \(10\pi\) and \(2\pi\) are coterminal angles. Therefore, the ordered pair on the unit circle, intersecting the terminal side of \(\theta = 10\pi\) is \((1, 0)\).
Try It! (Exercises)
For #1-10, A standard angle \(\theta\) is given in radians. State the reference angle \(\hat{\theta}\) in radians.
- \(\theta = \dfrac{11\pi}{6}\)
- \(\theta = \dfrac{7\pi}{9}\)
- \(\theta = \dfrac{11\pi}{7}\)
- \(\theta = 2\) radians
- \(\theta = −\dfrac{5\pi}{6}\)
- \(\theta = −\dfrac{5\pi}{4}\)
- \(\theta = \dfrac{9\pi}{4}\)
- \(\theta = \dfrac{17\pi}{6}\)
- \(\theta = 10\) radians
- \(\theta = −\dfrac{6\pi}{5}\)
For #11-20, the terminal side of the given standard angle, \(\theta\), intersects the unit circle at a point. State the ordered pair of the intersection.
- \(\theta = \dfrac{7\pi}{6}\)
- \(\theta = \dfrac{4\pi}{3}\)
- \(\theta = \dfrac{11\pi}{3}\)
- \(\theta = \dfrac{7\pi}{2}\)
- \(\theta = 5\pi\)
- \(\theta = \dfrac{13\pi}{4}\)
- \(\theta = −\dfrac{7\pi}{6}\)
- \(\theta = −4\pi\)
- \(\theta = −\dfrac{11\pi}{4}\)
- \(\theta = −\dfrac{5\pi}{2}\)
For #21-27, a standard angle’s rotation is described in words. You are given several hints about its rotation. Note: a full revolution is \(2\pi\) radians (if counter-clockwise) or \(−2\pi\) radians (if clockwise). Find the measure of the angle described using radians.
- An angle has a counter-clockwise rotation. The angle does not make a full revolution. The angle’s terminal side is in QIII. The reference angle \(\hat{\theta} = \dfrac{\pi}{3}\).
- An angle has a counter-clockwise rotation. The angle does not make a full revolution. The angle’s terminal side is in QIV. The reference angle \(\hat{\theta} = \dfrac{\pi}{4}\).
- An angle has a counter-clockwise rotation. The angle does not make a full revolution. The angle’s terminal side is in QII. The reference angle \(\hat{\theta} = \dfrac{\pi}{6}\).
- An angle has a clockwise rotation. The angle does not make a full revolution. The angle’s terminal side is in QIV. The reference angle \(\hat{\theta} = \dfrac{\pi}{3}\).
- An angle has a clockwise rotation. The angle does not make a full revolution. The terminal side of the angle intersects the unit circle at point \((−1, 0)\).
- An angle has a counter-clockwise rotation. The angle rotates more than one full revolution. The terminal side of the angle intersects the unit circle at point \(\left(−\dfrac{\sqrt{2}}{2}, −\dfrac{\sqrt{2}}{2} \right)\).
- An angle has a counter-clockwise rotation. The angle rotates more than two full revolutions. The terminal side of the angle intersects the unit circle at point \(\left(−\dfrac{1}{2} , \dfrac{\sqrt{3}}{2} \right)\).


