4.2: Radian Measure and Arc Length

Learning Objectives

• Find the radian measure of the central angle given the radius and arc length.
• Convert an angle from degrees to radians or vice versa.
• Evaluate a trigonometric function using radians.
• Identify the reference angle for a given angle measured in radians.
• Solve an application involving arc length.

Imagine riding on a Ferris wheel with a radius of 100 feet, where each rotation takes eight minutes. We can use angles in a standard position to describe your location as you travel around the wheel. Figure \( \PageIndex{ 1 } \) shows the locations indicated by \(\theta = 0^{\circ}\), \(90^{\circ}\), \(180^{\circ}\), and \(270^{\circ}\).

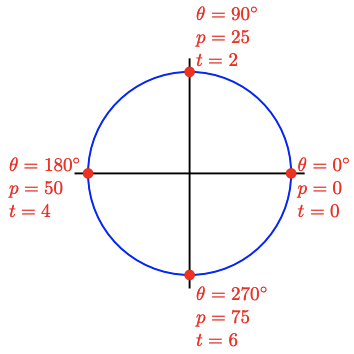
Figure \( \PageIndex{ 1 } \)

However, degrees are not the only way to specify a location on a circle. We could use a percent of one complete revolution¹ and label the same locations by \(p = 0\), \(p = 25\), \(p = 50\), and \(p = 75\). Another option is to use the time elapsed so that, for this example, we would have \(t = 0\), \(t = 2\), \(t = 4\), and \(t = 6\) minutes (see Figure \( \PageIndex{ 1 } \)).

Another helpful method uses distance traveled, or arc length, along the circle. In Figure \( \PageIndex{ 1 } \), how far have you traveled around the Ferris wheel at each of the locations shown, assuming you hopped onto the ride at \( \theta = 0^{\circ} \)?

Before we consider that question, let's agree on some vocabulary. An arc is a portion of a circle, and its length, quite naturally, is called arc length. An angle with vertex at the center of the circle is called a central angle, and a central angle whose sides meet the endpoints of an arc is said to subtend the arc or span the arc. If the arc represents a distance traveled, we sometimes refer to such an angle as the angle of displacement.

Arc Length

Recall that the circumference of a circle is given by the formula\[C=2 \pi r. \label{circlecircumference} \]

Another way to say this is that the circumference of a circle is proportional to its radius - increasing the radius of the circle increases the circumference and vice versa.

According to Equation \( \ref{circlecircumference} \), if we walk around the entire circumference of a circle, the distance we travel is the product of \(2 \pi\) and the radius, or approximately \( 6.28 \) times the radius. If we walk only part of the way around the circle, then the distance we travel depends also on the angle of displacement.

For example, an angle of \(45^{\circ}\) is \(\frac{1}{8}\) of a complete revolution, so the arc length, \(s\), from point \(A\) to point \(B\) in Figure \( \PageIndex{ 2 } \) is \(\frac{1}{8}\) of the circumference. Therefore,\[ s=\dfrac{1}{8}(2 \pi r)=\dfrac{\pi}{4} r. \nonumber \]

Figure \( \PageIndex{ 2 } \)

Similarly, the angle of displacement from point \(A\) to point \(C\) in Figure \( \PageIndex{ 3 } \) is \(\frac{3}{4}\) of a complete revolution, so the arc length along the circle from \(A\) to \(C\), shown below, is\[s=\dfrac{3}{4}(2 \pi r)=\dfrac{3\pi}{2} r.\nonumber \]

Figure \( \PageIndex{ 3 } \)

In general, the length of the arc spanned by an angle is proportional to the size of the angle for a given circle.

Theorem: Arc Length on a Circle

The length of the arc, \( s \), in a circle of radius \( r \), spanned by a fraction of a revolution, \( p \), is\[s = p \cdot(2 \pi r). \nonumber \]

The Ferris wheel in the introduction has circumference\[C=2 \pi(100) \approx 628 \text { feet,}\nonumber \]so in half a revolution, you travel approximately 314 feet around the edge. In one-quarter revolution, you travel approximately 157 feet.

To indicate the same four locations on the wheel by distance traveled, we would use \(s=0\), \(s \approx 157\), \(s \approx 314\), and \(s \approx 471\), as shown below.

Example \( \PageIndex{ 1 } \)

What length of arc is spanned by an angle of \(120^{\circ}\) on a circle of radius 12 centimeters?

Solution

Because \(\frac{120^{\circ}}{360^{\circ}}=\frac{1}{3}\), an angle of \(120^{\circ}\) is \(\frac{1}{3}\) of a complete revolution, as shown below.

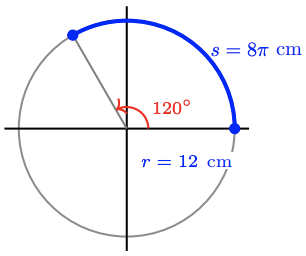
Using the arc length formula with \(r=12\), we find that\[s=\dfrac{1}{3}(2 \pi \cdot 12)=\dfrac{2 \pi}{3} \cdot 12=8 \pi \mathrm{ cm}\nonumber \]or about 25.1 cm.

Checkpoint \( \PageIndex{ 1 } \)

How far have you traveled around the edge of a Ferris wheel of radius 100 feet when you have turned through an angle of \(150^{\circ}\)?

Answer

Approximately 261.8 ft

Measuring Angles in Radians

If you think about measuring arc length, you will see that the degree measure of the spanning angle is not as important as the fraction of one revolution it covers. This observation suggests a new unit of measurement for angles, one that is better suited to calculations involving arc length. We'll make one change in our formula for arc length from

arc length = (fraction of one revolution) \(\cdot (2\pi r)\)

to

arc length = (fraction of one revolution \(\times 2\pi\)) \(\cdot r.\)

You might be asking yourself why we made such a silly change since these two formulas state the same thing (just with the parentheses in different spots).

The subtle difference between these two interpretations of arc length leads to an entirely new angular measurement system. We'll call the quantity in parentheses, (fraction of one revolution \(\times 2\pi\)), the radian measure of the angle that spans the arc.

Definition: Radian Measure

The radian measure of an angle is given by\[ \text{fraction of one revolution } \times 2 \pi . \nonumber \]

For example, one complete revolution (\(360^{\circ}\)) is equal to \(2 \pi\) radians, and one-quarter revolution (\(90^{\circ}\)) is equal to \(\frac{1}{4}(2 \pi) = \frac{\pi}{2}\) radians. Figure \( \PageIndex{ 4 } \) shows the radian measure of the quadrantal angles.

Figure \( \PageIndex{ 4 } \)

Note: Radian Measure is Universal

Unlike degree measure, which depends on a human-created construct dependent on either the number of days for the Earth to rotate around the sun or the base-60 numbering system used by the Babylonians (depending on which historical viewpoint of the creation of the degree measurement system you believe), radian measure makes sense on any planet and within any numbering system. That is, if an alien species were to arrive on Earth, radian measures for angles are likely something we would both have in common.

Example \( \PageIndex{ 2 } \)

What is the radian measure of an angle of \(120^{\circ}\)?

Solution

An angle of \(120^{\circ}\) is \(\frac{120^{ \circ }}{360^{ \circ }} = \frac{1}{3}\) of a complete revolution, as we saw in the previous example. Thus, an angle of \(120^{\circ}\) has a radian measure of \(\frac{1}{3}(2 \pi)\), or \(\frac{2 \pi}{3}\).

Checkpoint \( \PageIndex{ 2 } \)

What fraction of a revolution is \(\pi\) radians? How many degrees is that?

Answer

Half a revolution, \(180^{\circ}\)

Radian measure does not have to be expressed in multiples of \(\pi\). Remember that \(\pi \approx 3.14\), so one complete revolution is approximately 6.28 radians, and one-quarter revolution is \(\frac{1}{4}(2 \pi)=\frac{\pi}{2}\), or about 1.57 radians. Figure \( \PageIndex{ 5 } \) shows decimal approximations for the quadrantal angles.

Figure \( \PageIndex{ 5 } \)

Table \( \PageIndex{ 1 } \): Quadrantal Angles in Both Degrees and Radians

Degrees	Radians: Exact Values	Radians: Decimal Approximations
\(0^{\circ}\)	0	0
\(90^{\circ}\)	\(\dfrac{\pi}{2}\)	1.57
\(180^{\circ}\)	\(\pi\)	3.14
\(270^{\circ}\)	\(\dfrac{3\pi}{2}\)	4.71
\(360^{\circ}\)	\(2\pi\)	6.28

Memorize the Exact Radian Values of Common Angles

Because they are "benchmarks" for comparing angles, you should memorize the exact values of the angles in the previous table in radians!

Example \( \PageIndex{ 3 } \)

In which quadrant would you find an angle of 2 radians? An angle of 5 radians?

Solution

Look at Figure \( \PageIndex{ 5 } \). The second quadrant includes angles between \(\frac{\pi}{2}\) and \(\pi\), or approximately 1.57 and 3.14 radians, so 2 radians lies in the second quadrant. An angle of 5 radians is between 4.71 and 6.28, or between \(\frac{3 \pi}{2}\) and \(2 \pi\) radians, so it lies in the fourth quadrant.

Checkpoint \( \PageIndex{ 3 } \)

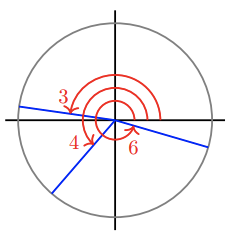
Draw a circle centered at the origin and sketch (in standard position) angles of approximately 3 radians, 4 radians, and 6 radians.

Answer

It turns out that measuring angles in radians is helpful for many applications besides calculating arc lengths, so we need to start thinking in radians. To help that process, we’ll first learn to convert between degrees and radians.

Converting Between Degrees and Radians

It is not difficult to convert the measure of an angle in degrees to its measure in radians or vice versa. One complete revolution is equal to \( 2 \pi \) radians or to \(360^{\circ}\), so\[2 \pi \text { radians }=360^{\circ}.\nonumber \]Dividing both sides of this equation by \(2 \pi\) radians or by \(360^{\circ}\) gives us a conversion factor:

Theorem: Unit Conversion for Angles

\[\begin{array}{rcl}
2 \pi \text{ radians} & = & 360^{\circ} \\
\end{array} \label{angleconversion} \]
\[\begin{array}{crclr}
\implies & 1 & = & \dfrac{180^{\circ}}{\pi \text{ radians}} & (\text{dividing both sides of Equation }\ref{angleconversion} \text{ by }2 \pi\text{ radians}) \\
\implies & \dfrac{\pi \text{ radians}}{180^{ \circ }} & = & 1 & (\text{dividing both sides of Equation } \ref{angleconversion} \text{ by }360^{\circ}) \\
\end{array} \nonumber \]

Example \( \PageIndex{ 4 } \)

1. Convert 3 radians to degrees.
2. Convert 3 degrees to radians.

Solutions

1. \[\begin{array}{rcl}
   3 \text{ radians} & = & 3 \text{ radians} \times (1) \\
   & = & 3 \text{ }\cancel{\text{radians}} \times \left( \dfrac{180^{\circ}}{\pi \text{ }\cancel{\text{radians}}} \right) \\
   & = & \dfrac{540^{\circ}}{\pi} \\
   & \approx & 171.9^{\circ} \\
   \end{array} \nonumber \]
2. \[\begin{array}{rcl}
   3^{\circ} & = & 3^{ \circ } \times (1) \\
   & = & 3^{\cancel{\circ}} \times\left(\dfrac{\pi \text{ radians}}{180^{\cancel{\circ} }}\right) \\
   & = & \dfrac{\pi}{60} \text{ radians} \\
   & \approx & 0.05 \text{ radians} \\
   \end{array} \nonumber \]

Technically speaking, a radian is what is known as a unitless measure. This is because, from the definition of radian measure, a radian is the product of a fraction of a revolution (no units) and \( 2 \pi \) (also, no units). Therefore, it is acceptable to answer Example \( \PageIndex{ 4b } \) with "approximately 0.05" instead of "approximately 0.05 radians." Moreover, there is no need to include the word "radian" when the context of the situation implies the constant is an angular measure (and the angular measure is not in degrees). For example, the solution to \( \PageIndex{ 4a } \) could have been written as\[\begin{array}{rcl}
3 & = & 3 \times (1) \\
& = & 3 \times \left( \dfrac{180^{\circ}}{\pi} \right) \\
& = & \dfrac{540^{\circ}}{\pi} \\
& \approx & 171.9^{\circ} \\
\end{array} \nonumber \]

Checkpoint \( \PageIndex{ 4 } \)

1. Convert \(60^{\circ}\) to radians. Give both an exact answer and an approximation to three decimal places.
2. Convert \(\frac{3 \pi}{4}\) to degrees.

Answers

1. \(\dfrac{\pi}{3} \approx 1.047\)
2. \(135^{\circ}\)

Reviewing Conversion Factors

You can review the use of conversion factors in the Algebra Refresher at the end of this section.

From our conversion factor we also learn that\[1 \text { radian }=\dfrac{180^{\circ}}{\pi} \approx 57.3^{\circ}.\nonumber \]

So while \(1^{\circ}\) is a relatively small angle, 1 radian is much larger (nearly \(60^{\circ}\), in fact). However, this is reasonable because there are only a little more than 6 radians in an entire revolution. An angle of 1 radian is shown above.

We'll soon see that, for many applications, it is easier to work entirely in radians. In fact, in the study of Calculus, you will find that radian measure must be used instead of degree measure.

For reference, Figure \( \PageIndex{ 6 } \) shows a radian protractor.

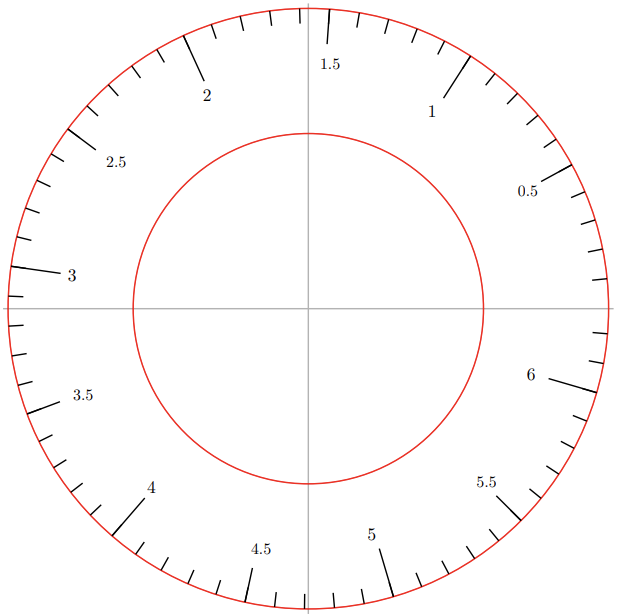
Figure \( \PageIndex{ 6 } \)

Quadrants and Reference Angles in Radians

Radian measure takes a bit to get used to, but you will soon find it easier to work with than degree measure. Understanding the acute special angles and quadrantal angles in radian measure, we now ask how to quickly determine in which quadrant an angle terminates. We also want to know the reference angle for a given angle in radian measure. We will focus on angles of the form \( \frac{n \pi}{d} \) for this discussion.²

A beneficial habit to get into when given an angle in radian measure of the form \( \frac{n \pi}{d} \) is to think in multiples of the denominator, \( d \). This is because \( \frac{d \pi}{d} = \pi \), \( \frac{2 d \pi}{d} = 2 \pi \), \( \frac{3 d \pi}{d} = 3 \pi \), and so on. If you sketch these angles, they terminate on either the positive or negative \( x \)-axis - this will be useful.

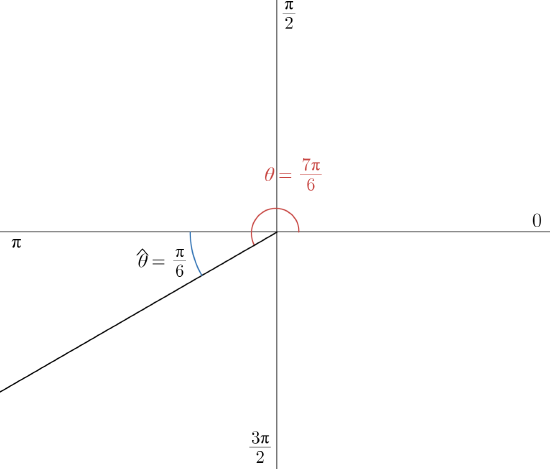
For example, if asked to find the quadrant in which \( \theta = \frac{7 \pi}{6} \) terminates, we consider that \( \theta \) is slightly more than \( \frac{6 \pi}{6} = \pi \) (which is equivalent to \( 180^{ \circ } \)). In fact, it is only \( \frac{1 \pi}{6} \) more than \( \frac{6 \pi}{6} = \pi \). Thus, to get to \( \theta \), we rotate past \( \pi \) and into quadrant three by the small amount of \( \frac{\pi}{6} \) radians. This small extra angle of rotation is the reference angle for \( \theta \). That is, the reference angle for \( \theta = \frac{7 \pi}{6} \) is \( \hat{\theta} = \frac{\pi}{6} \) (see the figure below).

This concept of using multiples of the denominator need not be limited to positive angles. For example, if \( \theta = -\frac{9 \pi}{5} \), we imagine rotating in the negative direction to \( -\frac{5 \pi}{5} = -\pi \); however, this is nowhere near \( -\frac{9 \pi}{5} \). Therefore, we continue until we get to \( -\frac{10 \pi}{5} = -2 \pi \). At this point, we will have rotated back to the positive \( x \)-axis, but we will have rotated slightly too far. Therefore, we back off (in the positive direction) by \( \frac{1 \pi}{5} \) to arrive at \( -\frac{9 \pi}{5} \), which terminates in the first quadrant. Hence, \( \theta = -\frac{9 \pi}{5} \in \mathrm{QI} \) with reference angle \( \hat{\theta} = \frac{\pi}{5} \) (see the figure below).

Example \(\PageIndex{5}\)

State the quadrant in which \( \beta = \frac{5 \pi}{3} \) terminates, state its reference angle and sketch.

Solution

\( \beta = \frac{5 \pi}{3} \) is almost all the way to \( \frac{6 \pi}{3} = 2\pi \), but we have to back off by \( \frac{\pi}{3} \). Hence, \( \frac{5\pi}{3} \in \mathrm{QIV} \) and \( \hat{\beta} = \frac{\pi}{3} \) (see the figure below).

Checkpoint \(\PageIndex{5}\)

State the quadrant in which \( \alpha = -\frac{17 \pi}{16} \) terminates, state its reference angle, and sketch.

Answer

\( \alpha \in \mathrm{QII} \) and \( \hat{\alpha} = \frac{\pi}{16} \)

Arc Length Formula

We now return to our calculation of arc length and see the first instance in which measuring angles in radians is useful. To calculate an arc length, we need only multiply the circle's radius by the radian measure of the spanning angle, \(\theta\). Look again at our formula for arc length:\[\text{arc length } = \left( \text{fraction of one revolution } \times 2 \pi \right) \cdot r \nonumber \]The quantity in parentheses, "fraction of one revolution \(\times 2 \pi\)," is the measure of the spanning angle in radians. Thus, if \(\theta\) is measured in radians, we have the following formula for arc length, \(s\).

Theorem: Arc Length Formula

On a circle of radius \(r\), the length \(s\) of an arc spanned by an angle \(\theta\) in radians is\[s=r \theta. \nonumber \]

The Radian Requirement

It is crucial to remember that the arc length formula, \( s = r \theta \), is only valid if \( \theta \) is in radians.

Thus, there is a special relationship between arc length and radians. An angle of 1 radian spans an arc on a circle equal to the radius of the circle, as shown in Figure \( \PageIndex{ 7 } \). Likewise, the length of any arc is just the product of the measure of its spanning angle in radians and the radius of the circle.

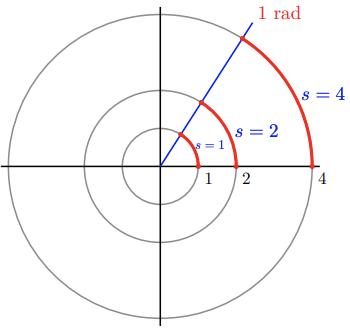
Figure \( \PageIndex{ 7 } \)

So, for instance, we can use the formula to find the arc length spanned by an angle of \(2.5\) radians on a circle of radius six inches:\[s = r \theta = \left(6 \, \text{inches}\right)(2.5) = 15 \text{ inches}.\nonumber \]Note that we didn't use the word "radians" when replacing \( \theta \) with \( 2.5 \). This is because, as we mentioned previously, radians is a unitless measure. Therefore, when performing unit analysis (which is the act of including units when performing computations to understand the meaning of the result of a series of computations), we leave the word "radians" off the angle.

We can also use the formula in the form \( \theta = \frac{s}{r} \) to find an angle that spans a given arc. For example, an arc length equal to one radius determines a central
angle of one radian, or approximately \( 57.3^{\circ} \).

In the following example, we use the arc length formula to compute a change in latitude on the Earth's surface.

Example \( \PageIndex{ 6 } \)

The Earth's radius is roughly 3,960 miles. If you travel 500 miles due north, how many degrees of latitude will you traverse? (Latitude is measured in degrees north or south of the equator.)

Solution

We think of the distance of 500 miles as an arc length on the surface of the Earth, as shown below. Substituting \(s=500\) and \(r=3960\) into the arc length formula gives\[\begin{array}{crcl}
& 500 \, \text{miles} & = & 3960 \, \text{miles} \times \theta \\
\implies & \dfrac{500 \, \cancel{\text{miles}}}{3960 \, \cancel{\text{miles}}} & = & \theta \\
\implies & \theta & \approx & 0.1263 \text { radians } \\
\end{array} \nonumber \]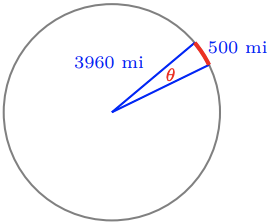

To convert the angle measure to degrees, we multiply by the conversion factor \(\frac{180^{\circ}}{\pi}\) to get\[0.1263\left(\dfrac{180^{\circ}}{\pi}\right) \approx 7.23^{\circ}\nonumber \]Your latitude has changed by about \(7.23^{\circ}\).

Checkpoint \( \PageIndex{ 6 } \)

The distance around the face of a large clock from 2 to 3 is five feet. What is the radius of the clock?

Answer

9.55 feet

Example \(\PageIndex{7}\)

The London Eye, located on the South Bank of the River Thames in London, is Europe's tallest Ferris wheel. In fact, when it first opened in 2000, it was the world's tallest Ferris wheel. It has a diameter of 120 meters. Interestingly, the London Eye rotates slowly enough that it never stops - riders easily step on and off at the wheel's bottom platform while the wheel is in motion.

Loi boards the London Eye to take in an elevated city view. If Loi has moved 80 meters along the circumference of the wheel, how many degrees has the London Eye rotated?

Solution

Parsing this question into language associated with our recent material, we have a circle of diameter 120 meters, which means the radius of the circle is 60 meters. Loi is moving through an arc of length 80 meters along the edge of this circle. Our task is to find the central angle that subtends this arc. In the formula\[ s = r \theta, \nonumber \]\( s = 80 \) meters and \( r = 60 \) meters. Therefore,\[ 80 \, \text{meters} = \left( 60 \, \text{meters} \right) \theta \implies \dfrac{80 \, \cancel{\text{meters}}}{60 \, \cancel{\text{meters}}} = \dfrac{4}{3} = \theta. \nonumber \]However, this angle is in radians. We must convert this to degrees.\[ \dfrac{4}{3} \times \dfrac{180^{ \circ }}{\pi} \approx 76.4^{ \circ }. \nonumber \]Hence, Loi moves through an approximate angle of \( 76.4^{ \circ } \).

 

Checkpoint \(\PageIndex{7}\)

A central angle in a circle of radius 6 cm cuts off an arc of length 24 cm. What is the radian measure of the angle? What is the degree measure?

Answer

\( 4 \, \text{radians} \approx 229^{ \circ }\)

Trigonometric Functions of Angles in Radians

Measuring angles in radians has other applications besides calculating arc length. One such use is evaluating trigonometric functions of angles in radians. Many applications in Trigonometry (and beyond) use radians for input values rather than degrees. For this reason, it is crucial to know the trigonometric values for the special angles, which you learned in degrees previously, when the angles are given in radians. Fortunately, the value of a trigonometric function is the same whether the angle is measured in radians or degrees.

For example, \(\frac{\pi}{3}\) radians is the same as \(60^{\circ}\), because \(\frac{\pi}{3} \cdot \frac{180^{\circ}}{\pi}=60^{\circ}\), so\[\sin \left(\dfrac{\pi}{3}\right)=\sin \left(60^{\circ}\right)=\dfrac{\sqrt{3}}{2}\nonumber \]The following table shows the radian measures for the special angles and the quadrantal angles, as well as the exact values of the sine, cosine, and tangent at these angles.

\( \theta \) in Degrees	\( \theta \) in Radians	\( \sin\left( \theta \right) \)	\( \cos\left( \theta \right) \)	\( \tan\left( \theta \right) \)
\(0^{\circ}\)	\( 0 \)	\( 0 \)	\( 1 \)	\( 0 \)
\(30^{\circ}\)	\(\dfrac{\pi}{6}\)	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{1}{\sqrt{3}}\)
\(45^{\circ}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{1}{\sqrt{2}}\)	\(\dfrac{1}{\sqrt{2}}\)	\( 1 \)
\(60^{\circ}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{1}{2}\)	\(\sqrt{3}\)
\(90^{\circ}\)	\(\dfrac{\pi}{2}\)	\( 1 \)	\( 0 \)	undefined
\( 180^{ \circ } \)	\( \pi \)	\( 0 \)	\( -1 \)	\( 0 \)
\( 270^{ \circ } \)	\( \dfrac{3 \pi}{2} \)	\( -1 \)	\( 0 \)	undefined
\( 360^{ \circ } \)	\( 2\pi \)	\( 0 \)	\( 1 \)	\( 0 \)

You should memorize these function values and be able to use them to find trigonometric values for the special angles in all four quadrants, as they will appear frequently throughout the rest of Trigonometry.

Example \(\PageIndex{8}\)

Compute the value of \( \csc\left( \frac{\pi}{3} \right) \).

Solution

Our identities still hold - working in radians does not change that fact. Therefore, by the Reciprocal Identities,\[ \csc\left( \frac{\pi}{3} \right) = \dfrac{1}{\sin\left( \frac{\pi}{3} \right)} = \dfrac{1}{\sqrt{3}/2} = \dfrac{2}{\sqrt{3}}. \nonumber \]

Checkpoint \(\PageIndex{8}\)

Compute the value of \( \cot\left( \frac{\pi}{4} \right) \).

Answer

1

As before, we use reference angles to define the trigonometric functions for angles greater than \(90^{\circ}\).

Example \( \PageIndex{ 9} \)

Give exact values for the following.

1. \(\tan \left(\dfrac{2 \pi}{3}\right)\)
2. \(\cos \left(\dfrac{5 \pi}{4}\right)\)

Solutions

1. The reference angle for \(\theta = \frac{2 \pi}{3}\) is \(\hat{\theta} = \pi-\frac{2 \pi}{3}=\frac{\pi}{3}\), and the tangent is negative in the second quadrant. (See the figure below.) Thus, \(\tan \left(\frac{2 \pi}{3}\right)=-\tan \left(\frac{\pi}{3}\right)=-\sqrt{3}\).

b The reference angle for \(\theta = \frac{5 \pi}{4}\) is \(\hat{\theta} = \frac{5 \pi}{4}-\pi=\frac{\pi}{4}\), and the cosine is negative in the third quadrant, so \(\cos \left(\frac{5 \pi}{4}\right)=-\cos \left(\frac{\pi}{4}\right)=-\frac{1}{\sqrt{2}}\).

Checkpoint \( \PageIndex{ 9} \)

Give exact values for the following.

1. \(\sin \left(\dfrac{5 \pi}{6}\right)\)
2. \(\tan \left(\dfrac{7 \pi}{4}\right)\)

Answers

1. \(\dfrac{1}{2}\)
2. \(-1\)

---

Footnotes

¹ The word "revolution" will be used extensively from this point forward. Some texts use "rotation."

² Angles in radians need not have a \( \pi \) attached to them, but it does help when determining the quadrant in which the angle terminates. Therefore, we restrict ourselves to angles of the form \( \frac{n \pi}{d} \) for this short discussion.

---

Skills Refresher

Review the following skills you will need for this section.

Skills Refresher

For Problems 1 - 4, use the appropriate conversion factor to convert units.

1. \(\dfrac{1 \text{ mile}}{1.609 \text{ kilometers}} = 1\)

   1. 10 miles = ______ km

   2. 50 km = ______ miles

2. \(\dfrac{1 \text{ acre}}{0.405 \text{ hectare}} = 1\)

   1. 40 acres = ______ hectares

   2. 5 hectares = ______ acres

3. \(\dfrac{1 \text{ horsepower}}{746 \text{ watts}} = 1\)

   1. 250 horsepower = ______ watts

   2. 1000 watts = ______ horsepower

4. \(\dfrac{ 1 \text{ troy ounce}}{480 \text{ grains}} = 1\)

   1. 0.5 troy oz = ______ grains

   2. 100 grains = ______ troy oz

For Problems 5 - 8, determine how many degrees are in each fraction of one complete revolution.

5. \(\dfrac{1}{4}\)

6. \(\dfrac{1}{5}\)

7. \(\dfrac{1}{6}\)

8. \(\dfrac{1}{8}\)

Answers

1. 1. 16.09 km

   2. 31.08 mi

2. 1. 16.2 hectares

   2. 12.35 acres

3. 1. 186,500 watts

   2. 1.34 horsepower

4. 1. 240 grains

   2. 0.21 troy oz

5. \(90^{\circ}\)

6. \(72^{\circ}\)

7. \(60^{\circ}\)

8. \(45^{\circ}\)

---

Homework

Vocabulary Check

1. Unlike degree measure, radian measure is a ___ measure (i.e., radian measure does not require a measurement symbol).

2. An angle with vertex at the center of the circle is called a(n) ___.

3. A central angle whose sides meet the endpoints of an arc is said to ___ the arc. Another way to say this is the angle ___ the arc.

4. The ___ length is the distance along the edge of a circle subtended by a central angle \( \theta \).

5. The product of \( 2 \pi \) and the fraction of one revolution cut out by the angle \( \theta \) is named the ___ measure of the angle.

Concept Check

6. The length of a circular arc depends on what two variables?

7. Define the radian measure of an angle.

8. What is the conversion factor from radians to degrees?

9. On a unit circle, the length of an arc is equal to what other quantity?

True or False? For Problems 10 - 15, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.

10. The distance we travel around a circle of diameter \( d \) is proportional to the angle of displacement. In fact,\[\text{arc length } = \text{(fraction of one revolution)} \cdot (\pi d)\nonumber \]

11. We measure angles in radians when we work with arc length.

12. An arc length equal to one radius determines a central angle of one degree.

13. An angle given in radian measure must be written as \( k \pi \), where \( k \) is a real number.

14. \( \dfrac{180^{\circ}}{\pi \text{ radians}} = 1 \)

15. On a circle of radius \(r\), the length \(s\) of an arc spanned by an angle \(\theta\) is \(s = r \theta\).

Basic Skills

16.  

    Radians	0	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{3\pi}{4}\)	\(\pi\)	\(\dfrac{5\pi}{4}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{7\pi}{4}\)	\(2\pi\)
    Degrees

    1. Convert each angle to degrees.

    2. Sketch each angle on a circle like this, and label in radians.

       

17.  

    Radians

    0

    \(\dfrac{\pi}{6}\)

    \(\dfrac{\pi}{3}\)

    \(\dfrac{\pi}{2}\)

    \(\dfrac{2\pi}{3}\)

    \(\dfrac{5\pi}{6}\)

    \(\pi\)

    \(\dfrac{7\pi}{6}\)

    \(\dfrac{4\pi}{3}\)

    \(\dfrac{3\pi}{2}\)

    \(\dfrac{5\pi}{3}\)

    \(\dfrac{11\pi}{6}\)

    \(2\pi\)

    Degrees

    1. Convert each angle to degrees.

    2. Sketch each angle on a circle like this, and label in radians.

       

For Problems 18 - 21, express each fraction of one complete rotation in degrees and radians.

18.  

    

    1. \(\dfrac{1}{3}\)

    2. \(\dfrac{2}{3}\)

    3. \(\dfrac{4}{3}\)

    4. \(\dfrac{5}{3}\)

19.  

    

    1. \(\dfrac{1}{5}\)

    2. \(\dfrac{2}{5}\)

    3. \(\dfrac{3}{5}\)

    4. \(\dfrac{4}{5}\)

20.  

    

    1. \(\dfrac{1}{8}\)

    2. \(\dfrac{3}{8}\)

    3. \(\dfrac{5}{8}\)

    4. \(\dfrac{7}{8}\)

21.  

    

    1. \(\dfrac{1}{12}\)

    2. \(\dfrac{1}{6}\)

    3. \(\dfrac{5}{12}\)

    4. \(\dfrac{5}{6}\)

For Problems 22 and 23, label each angle in standard position with radian measure (assume the angles shown are special angles).

22. Rotate counter-clockwise from 0.

    

23. Rotate clockwise from 0.

    

For Problems 24 and 25, give a decimal approximation to hundredths for each angle in radians.

24.  

    1. \(\dfrac{\pi}{6}\)

    2. \(\dfrac{5 \pi}{6}\)

    3. \(\dfrac{7 \pi}{6}\)

    4. \(\dfrac{11 \pi}{6}\)

25.  

    1. \(\dfrac{\pi}{4}\)

    2. \(\dfrac{\pi}{4}\)

    3. \(\dfrac{5 \pi}{4}\)

    4. \(\dfrac{7 \pi}{4}\)

26. Locate and label each angle from Problem 24 on the unit circle below. (The circle is marked off in tenths of a radian.)

    

27. Locate and label each angle from Problem 25 on the unit circle below. (The circle is marked off in tenths of a radian.)

    

Choose the best decimal approximation for each angle in radians in Problems 28 - 35 from the list below. Do not use a calculator; use the fact that \(\pi\) is a little greater than 3.\[0.52, 0.79, 2.09, 2.36, 2.62, 3.67, 5.24, 5.50\nonumber \]

28. \(\dfrac{2 \pi}{3}\)

29. \(\dfrac{\pi}{4}\)

30. \(\dfrac{5 \pi}{6}\)

31. \(\dfrac{5 \pi}{3}\)

32. \(\dfrac{\pi}{6}\)

33. \(\dfrac{7 \pi}{4}\)

34. \(\dfrac{3 \pi}{4}\)

35. \(\dfrac{7 \pi}{6}\)

For Problems 36 - 39, state in which quadrant each angle lies.

36.  

    1. \(\dfrac{\pi}{4}\)

    2. \(\dfrac{\pi}{4}\)

    3. \(\dfrac{5 \pi}{4}\)

    4. \(\dfrac{7 \pi}{4}\)

37.  

    1. \(\dfrac{\pi}{4}\)

    2. \(\dfrac{\pi}{4}\)

    3. \(\dfrac{5 \pi}{4}\)

    4. \(\dfrac{7 \pi}{4}\)

38.  

    1. \(\dfrac{\pi}{4}\)

    2. \(\dfrac{\pi}{4}\)

    3. \(\dfrac{5 \pi}{4}\)

    4. \(\dfrac{7 \pi}{4}\)

39.  

    1. \(\dfrac{\pi}{4}\)

    2. \(\dfrac{\pi}{4}\)

    3. \(\dfrac{5 \pi}{4}\)

    4. \(\dfrac{7 \pi}{4}\)

For Problems 40 - 43, complete the table.

40.  

    Radians	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{3}\)
    Degrees

41.  

    Radians	\(\dfrac{2\pi}{3}\)	\(\dfrac{3\pi}{4}\)	\(\dfrac{5\pi}{6}\)
    Degrees

42.  

    Radians	\(\dfrac{7\pi}{6}\)	\(\dfrac{5\pi}{4}\)	\(\dfrac{4\pi}{3}\)
    Degrees

43.  

    Radians	\(\dfrac{5\pi}{3}\)	\(\dfrac{7\pi}{4}\)	\(\dfrac{11\pi}{6}\)
    Degrees

For Problems 44 and 45, convert to radians. Write the answer in exact form and then give approximations rounded to the nearest hundredths.

44.  

    1. \(75^{\circ}\)

    2. \(236^{\circ}\)

    3. \(327^{\circ}\)

    4. \( 143^{ \circ } \, 40^{\prime} \)

45.  

    1. \(138^{\circ}\)

    2. \(194^{\circ}\)

    3. \(342^{\circ}\)

    4. \( 281^{ \circ } \, 15^{\prime} \)

For Problems 46 and 47, convert to degrees. Round answers to the nearest tenth.

46.  

    1. 0.8

    2. 3.5

    3. 5.1

47.  

    1. 1.1

    2. 2.6

    3. 4.6

For Problems 48 - 57, state the quadrant in which the angle terminates and give the reference angle (in radians).

48. \( \frac{\pi}{3} \)

49. \( \frac{3\pi}{4} \)

50. \( \frac{9\pi}{8} \)

51. \( \frac{21\pi}{22} \)

52. \( -\frac{5\pi}{6} \)

53. \( -\frac{5\pi}{3} \)

54. \( \frac{11\pi}{4} \)

55. \( -\frac{15\pi}{7} \)

56. \( 2.4 \)

57. \( -3.1 \)

For Problems 58 - 63, find an angle in each quadrant, rounded to tenths, with the same reference angle as the angle given in radians.

58. 5.8

59. 2.9

60. 3.7

61. 5.1

62. 1.8

63. 4.4

For Problems 64 - 69, use the arc length formula to answer the questions. Round answers to hundredths.

64. Find the arc length spanned by an angle of \(80^{\circ}\) on a circle of radius 4 inches.

65. Find the arc length spanned by an angle of \(200^{\circ}\) on a circle of radius 18 feet.

66. Find the radius of a circle if an angle of \(250^{\circ}\) spans an arc length of 18 meters.

67. Find the radius of a circle if an angle of \(20^{\circ}\) spans an arc length of 0.5 kilometers.

68. Find the angle subtended by an arc length of 28 centimeters on a circle of diameter 20 centimeters.

69. Find the angle subtended by an arc length of 1.6 yards on a circle of diameter 2 yards.

For Problems 70 - 84, find the exact value of the trigonometric function. Do not use a calculator!

70. \( \sin\left( \dfrac{\pi}{3} \right) \)

71. \( \cos\left( \dfrac{\pi}{6} \right) \)

72. \( \tan\left( \dfrac{\pi}{4} \right) \)

73. \( \csc\left( \dfrac{\pi}{4} \right) \)

74. \( 2\sec\left( \dfrac{\pi}{3} \right) \)

75. \( \cot\left( \dfrac{\pi}{6} \right) \)

76. \( -\sin\left( \dfrac{5\pi}{6} \right) \)

77. \( \cos\left( \dfrac{4\pi}{3} \right) \)

78. \( \tan\left( \dfrac{11\pi}{6} \right) \)

79. \( 3\csc\left( -\dfrac{4\pi}{3} \right) \)

80. \( \sec\left( -\dfrac{3\pi}{4} \right) \)

81. \( -\pi \cot\left( -\dfrac{13\pi}{6} \right) \)

82. \( \sin\left( \dfrac{\pi}{2} \right) \)

83. \( \cos\left( \pi \right) \)

84. \( \tan\left( \dfrac{3\pi}{2} \right) \)

Synthesis Questions

For Problems 85 - 93, find the exact value of the expression for \( x = \frac{\pi}{6} \).

85. \( \sin\left( 2x \right) \)

86. \( \cos\left( 3x \right) \)

87. \( \dfrac{1}{3} \sin\left( 5x \right) \)

88. \( 6 - \sin\left( x \right) \)

89. \( \dfrac{2}{3} + \tan\left( \dfrac{3}{2}x \right) \)

90. \( \sin\left( \pi - x \right) \)

91. \( \cos\left( \pi + 2x \right) \)

92. \( 3 \sin\left( 2x + \dfrac{\pi}{3} \right) \)

93. \( -2 + \dfrac{3}{4} \cos\left( 7x - \dfrac{\pi}{2} \right) \)

94.  

    1. Sketch a circle of radius 4 units, and mark the positions of 1, 2, 3, 4, 5, and 6 radians on the circle.

    2. On a circle of radius 4 feet, find the arc length determined by each angle in radians.

       \(\theta\)	1	2	3	4	5	6
       \(s\)

    3. Graph \(\theta\) against \(s\). What is the slope of the graph?

       

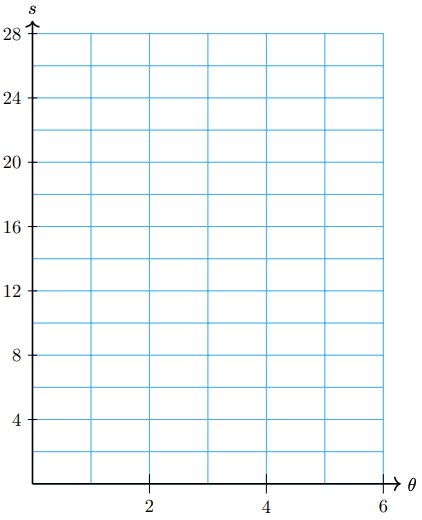
    4. If you double the angle, what happens to the arc length? What happens if you triple \(\theta\)?

95.  

    1. Sketch several concentric circles with increasing radii, and draw an angle of 2 radians through all of them.

    2. Find the arc length determined by an angle of 2 radians on circles of given radius.

       \(r\)	1	2	3	4	5	6
       \(s\)

    3. Graph \(s\) against \(r\). What is the slope of the graph?

       

    4. If you double the radius \(r\), what happens to the arc length? What happens if you triple \(r\)?

96. Recall that to calculate a fraction of a revolution in degrees, we divide the angle by \(360^{\circ}\). For example, \(90^{\circ}\) is \(\frac{1}{4}\) of a revolution because \(\frac{90^{\circ}}{360^{\circ}}=\frac{1}{4}\).

    1. Write an expression that gives the fraction of a revolution for an angle \(\theta\) in radians.

    2. Use your expression to calculate what fraction of a revolution is represented by each of the following angles: \(\theta=\frac{3 \pi}{4}, \quad \theta=\frac{5 \pi}{3}, \quad \theta=\frac{7 \pi}{6}\).

Applications

For Problems 97 - 101, use the arc length formula to answer the questions.

97. Big Ben.

    1. Through how many radians does the minute hand of a clock sweep between 9:05 pm and 9:30 pm?

    2. The dial of Big Ben's clock in London is 23 feet in diameter. How long is the arc traced by the minute hand between \(9: 05 \mathrm{pm}\) and \(9: 30 \mathrm{pm}\)?

98. Floral Clock. The largest clock ever constructed was the Floral Clock in the garden of the 1904 World's Fair in St. Louis. The hour hand was 50 feet long, the minute hand was 75 feet long, and the radius of the clock's face was 112 feet.

    1. If you started at the 12 and walked 500 feet clockwise around the clock face, through how many radians would you walk?

    2. If you started your walk at noon, how long would it take the minute hand to reach your position? How far did the tip of the minute hand move in its arc?

99. The Foucault Pendulum. In 1851 Jean-Bernard Foucault demonstrated the rotation of the earth with a pendulum installed in the Pantheon in Paris. Foucault's pendulum consisted of a cannonball suspended on a 67 meter wire, and it swept out an arc of 8 meters on each swing. Through what angle did the pendulum swing? Give your answer in radians and then in degrees, rounded to the nearest hundredth.

100. Linear Distance. A wheel with radius 40 centimeters is rolled a distance of 1000 centimeters on a flat surface. Through what angle has the wheel rotated? Give your answer in radians and then in degrees, rounded to one decimal place.

101. Distance Between Cities. Cosumnes River College (Sacramento, California) and Stony Brook University (Stony Brook, New York) are 2,544 miles apart along the surface of the Earth. Assuming that the radius of the Earth is 3,963 miles, find the radian measure of the central angle having vertex at the center of the Earth that has Cosumnes River College on one side and Stony Brook University on the other.