Chapter 4: Radian Measure and the Circular Functions

Have you ever wondered why we divide the circle into 360 degrees? Nobody knows the answer, but it may have started around 600 BCE with the Babylonians.

The Babylonians lived between the Tigris and Euphrates rivers in present-day Turkey and Syria. They kept written records using a stylus to press cuneiform, or wedge-shaped, symbols into wet clay tablets, which were then baked in the sun. Thousands of these tablets have survived and give us detailed information about the mathematical practices of the time.

The Babylonians used a base 60 number system because the number 60 has many factors. They did not invent decimal fractions, so they found it challenging to deal with remainders when dividing. But 60 can be divided evenly by 2, 3, 4, 5, and 6, which made calculations with common fractions much more manageable.

We still have traces of their base 60 system: there are 60 seconds in a minute and 60 minutes in an hour.

In Geometry, Babylonian mathematicians used the corner of an equilateral triangle as their basic unit of angular measure. Naturally, they divided that angle into 60 smaller angles. Now, suppose the corners of six equilateral triangles are placed together. In that case, they form a complete circle, so there are six times 60, or 360, degrees of arc in a circle.

During the reign of Nebuchadnezzar, using the tools and technology available to them, Babylonian astronomers calculated that a complete year numbered 360 days. This made dividing the circle into 360 degrees even more helpful.

The number 360 is not fundamental to the nature of a circle. If ancient civilizations had defined the whole circle as some other number of degrees, we’d probably be using that number today.

But why do we need another, different way to measure angles? In this chapter, we’ll study radian measure, which initially may seem awkward and unnatural. As a hint, consider that although 360 is not fundamental to circles, the number \(\pi\) is.

Radians connect the measure of an angle with the arc length it cuts out on a circle.

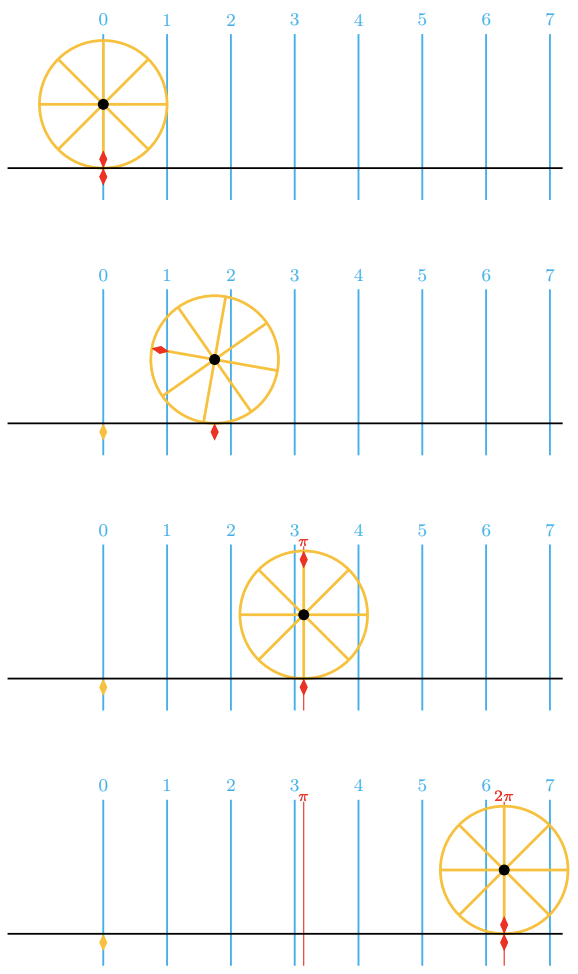
Imagine a circle with a radius of 1 unit rolling along a straight line. The circumference of a circle is \(2 \pi\) times the length of its radius, so when the circle has turned through one complete revolution, it has traveled a distance of \(2 \pi\) units. When the circle has turned through half a revolution, it has traveled a distance of \(\pi\) units.

In radian measure, the angle through which the circle has turned is equal to the distance the circle has traveled or, put another way, the length of the arc that has unrolled on the line.

Roger Cotes, an English mathematician who worked closely with Isaac Newton, developed the idea of radian measure. He described the radian in everything but name and recognized its naturalness as a unit of angular measure.

The term radian first appeared in print on June 5, 1873, on an exam written by James Thomson, the brother of Lord Kelvin, at Queen’s College in Belfast.

In calculus and most other branches of mathematics beyond practical Geometry, angles are nearly always measured in radians. Because radians arise naturally when dealing with circles, essential relationships are expressed more concisely in radians. In particular, results involving trigonometric functions are more straightforward when the variables are expressed in radians.