4.3: The Trigonometric Functions - Unit Circle Definition
- Page ID
- 145927
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This section is designed assuming you understand the following topics from Algebra.
- Equations of circles
- Evaluate a trigonometric function using the unit circle
- Find the value of a trigonometric function given a point on the unit circle.
- Use a calculator to approximate the value of a trigonometric function for an angle in radians.
- Use the unit circle to answer a conceptual question about a trigonometric function.
We now venture into the third and final definition of the trigonometric functions. Many students have already encountered this definition from their high school precalculus course; however, there are three reasons I have held off on introducing the trigonometric functions via this definition until now:
- In my experience, learning the unit circle definition of the trigonometric functions before the right triangle definition leads to more memorization and a less accurate understanding of the trigonometric functions.
- Unit circle trigonometry is theoretically more challenging to grasp. It has two interpretations - one in terms of angles and the other in terms of arc lengths (and, as such, most students who learn it before right triangle trigonometry tend to have a weak grasp of the subject).
- Unit circle trigonometry relies on radian measure.
Connecting the Sine and Cosine Functions to the Unit Circle
Figure \( \PageIndex{ 1a } \) below shows an angle of \(30^{\circ}\) in standard position in a circle of radius \(2\). The hypotenuse of its reference triangle is the radius of the circle, so the legs of the triangle have lengths \(1\) and \(\sqrt{3}\). The coordinates of the point \(P\) where the terminal side meets the circle are thus \((\sqrt{3}, 1)\).1
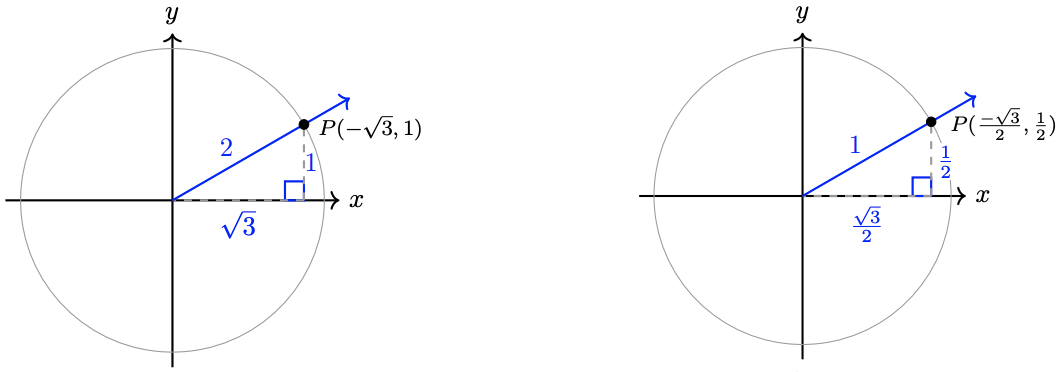
Figure \( \PageIndex{ 1a } \) (left) and \( \PageIndex{ 1b } \) (right)
Consider the unit circle in Figure \( \PageIndex{ 1b } \). In this figure, the hypotenuse of the reference triangle for \(30^{\circ}\) has length \(1\). What are the coordinates of the point \(P\) where the terminal side meets the circle? Each side of this triangle is half the length of the sides of the similar triangle in Figure (a), so the coordinates of \(P\) are \(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\).2
You should recognize the coordinates of the point \(P\) as \( \left( \cos\left( 30^{ \circ } \right), \sin\left( 30^{ \circ } \right) \right) \). In fact, from the coordinate definition of the trigonometric functions, we should not be surprised to see that, given the point \( \left( x,y \right) \) on the unit circle on the terminal side of the angle \( \theta \),\[\cos \left(\theta\right)=\dfrac{x}{r}=\dfrac{x}{1}=x \quad \text { and } \quad \sin \left(\theta\right)=\dfrac{y}{r}=\dfrac{y}{1}=y\nonumber \]We have discovered an important property of unit circles.
Let \( \theta \) be an angle in standard position, and suppose the terminal side of \( \theta \) intersects the unit circle at the point \( P\left( x,y \right) \). Then\[ \cos\left( \theta \right) = x \quad \text{and} \quad \sin\left( \theta \right) = y. \nonumber \]
While this lemma is not entirely profound, it will lead to a more significant concept. Before we get there, let's use the lemma in an example.
Find the coordinates of point \(P\) on the unit circle below.
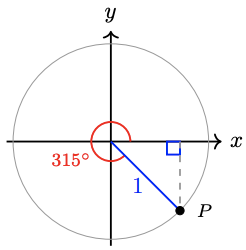
- Solution
-
The coordinates of \(P\) are given by\[x=\cos \left(315^{\circ}\right), \quad y=\sin \left(315^{\circ}\right).\nonumber \]The reference angle for \(315^{\circ}\) is \(360^{\circ}-315^{\circ}=45^{\circ}\), so the trigonometric functions of \(315^{\circ}\) are the same as the functions for \(45^{\circ}\), up to sign.
Because \(315^{\circ}\) is in the fourth quadrant, we have \(\cos \left(315^{\circ}\right)=\frac{1}{\sqrt{2}}\) and \(\sin \left(315^{\circ}\right)=-\frac{1}{\sqrt{2}}\). Thus, the coordinates of \(P\) are \(\left(\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}\right)\).
Find the sine, cosine, and tangent of the angle \(\varphi\) shown below.
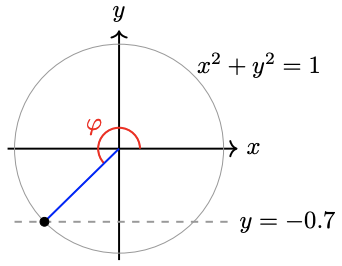
- Answer
-
\(\sin \left(\varphi\right)=-0.7000, \cos \left(\varphi\right) \approx -0.7141, \tan \left(\varphi\right) \approx 0.9802\)
A Reminder of Radian Measure and Arc Length
For the remainder of this chapter, we will focus on using radians instead of degrees. This change will greatly increase the utility of the trigonometric functions. To illustrate this, and as a refresher of previously learned material, recall that the radius of a unit circle is \(1\). Therefore, the arc length formula becomes \(s=r \theta = (1) \theta = \theta\). Thus, on a unit circle, an arc of length 1 determines a central angle of 1 radian. Moreover, the measure of an angle in radians is equal to the length of the arc it spans. In other words, if we walk along the edge of a circle of radius 1, each time we travel through an arc length equivalent to one radius, we have rotated through an angle of one radian.
You are walking on a trail around a circular pond with a radius of one mile. You have hiked for four miles. Sketch your location now.
- Solution
-
The pond is a unit circle, so you have traversed an angle in radians equal to the arc length traveled, 4 miles. An angle of 4 radians is in the middle of the third quadrant relative to your starting point, more than halfway but less than three-quarters around the pond.

An ant walks around the rim of a circular birdbath of a radius of 1 foot. How far has the ant walked when it has turned through an angle of \(210^{\circ}\)?
- Answer
-
3.67 ft
Trigonometric Functions of Real Numbers and the Unit Circle Definition
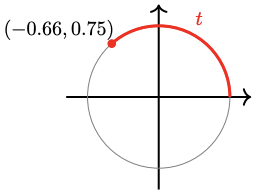
We now venture into a more theoretical area of Trigonometry. For this discussion, we will denote the arc length of a circle subtended by the angle \( \theta \) with the letter \( t \) instead of \( s \) (for no better reason than tradition).
Consider the unit circle shown in Figure \( \PageIndex{ 2 } \) below, and the angle \(\theta\) determined by the arc of length \(t\). The radian measure of \(\theta\) is the same as the length \(t\) of the arc. For example, in this figure \(\theta=t=2\).

Figure \( \PageIndex{ 2 } \): Traversing the unit circle
Therefore, as long as we restrict our conversation to the unit circle, instead of thinking of the sine or cosine as a function of an angle, \( \theta \), we can change our perspective and think of these as functions of the length of an arc, \( t \), along the unit circle. Since the arc length is not an angle but instead a simple real number, we are evaluating the trigonometric function at a real number.
This brings us to our third and final definition of the trigonometric functions.
Let \( P\left( x,y \right) \) be a point on the unit circle, and let \( t \) be the arc length from the point \( \left( 1,0 \right) \) to \( P \) along the circumference of the unit circle. The trigonometric functions of the real number \( t \) are defined as follows: \[ \begin{array}{|ccc|ccc|}
\hline
\text{Function} & & \text{Ratio} & \text{Function} & & \text{Ratio} \\
\hline
\sin\left( t \right) & = & y & \csc\left( t \right) & = & \dfrac{1}{y} \\
\cos\left( t \right) & = & x & \sec\left( t \right) & = & \dfrac{1}{x} \\
\tan\left( t \right) & = & \dfrac{y}{x} & \cot\left( t \right) & = & \dfrac{x}{y} \\
\hline \end{array} \nonumber \]
We sometimes call the trigonometric functions of arc length, \(\sin (t)\) and \(\cos (t)\), the circular functions because they are defined by the coordinates of points on a unit circle.
We can think of the definition this way: to find the sine or cosine of a real number \(t\), we draw an arc of length \(t\) on a unit circle and then find the sine or cosine of the angle \(\theta\) determined by the arc.
In practice, there is no difference between finding the value of a trigonometric function at the number 2 and the value at the angle of 2 radians. In each case, we set the calculator to Radian mode and evaluate, for example,\[\mathrm{COS} \, 2 \approx -0.4161 \quad \text { and } \quad \mathrm{SIN} \, 2 \approx 0.9093. \nonumber \]
So, in some sense, a trigonometric function of a radian is the same as a trigonometric function of a real number. This result is so important that it bears repeating:
To find the value of a trigonometric function of a real number \(t\), we find the value of the trigonometric function of the
angle \(t\) radians.
Let \( t = \frac{2 \pi}{3} \) be the length of the arc along the unit circle from the point \( \left( 1,0 \right) \) to \( P\left( x,y \right) \). Evaluate each of the following functions.
- \( \sin\left( t \right) \)
- \( \cot\left( t \right) \)
- Solutions
-
- Since \( t = \frac{2 \pi}{3} \), we are being asked to evaluate \( \sin\left( \frac{2 \pi}{3} \right) \). As stated before, a trigonometric function's value at a real number (an arc length along the unit circle) and the equivalent radian angle are the same. Thus,\[ \sin\left( \dfrac{2\pi}{3} \right) = \sin\left( \dfrac{\pi}{3} \right) = \dfrac{\sqrt{3}}{2}. \nonumber \]
- As in part a., we just evaluate\[ \cot\left( \dfrac{2 \pi}{3} \right) = - \cot\left( \dfrac{\pi}{3} \right) = -\dfrac{1}{\sqrt{3}}. \nonumber \]
Evaluate \( \sec\left( t \right) \), where \( t = \frac{5 \pi}{4} \) is the arc length along the unit circle from the point \( \left( 1,0 \right) \).
- Answer
-
\( -\sqrt{2} \)
Find the coordinates of the terminal point, \(P\), of an arc of length \(t\) starting at \((1,0)\) on a unit circle.
- \(t=\frac{\pi}{2}\)
- \(t=\frac{5 \pi}{6}\)
- Solutions
-
- On a unit circle, the coordinates of \(P\) are \(\left(\cos \left(\frac{\pi}{2}\right), \sin \left(\frac{\pi}{2}\right)\right)\), so\[x=\cos \left(\dfrac{\pi}{2}\right)=0 \quad \text { and } \quad y=\sin \left(\dfrac{\pi}{2}\right)=1 \nonumber \]The coordinates of \(P\) are \((0,1)\), as shown below.
(We could also observe that an arc of length \(\frac{\pi}{2}\) is one-quarter of a unit circle, so the point \(P\) sits at the twelve o'clock position on the circle.)
- The coordinates of \(P\) are \(\left(\cos \left(\frac{5 \pi}{6}\right), \sin \left(\frac{5 \pi}{6}\right)\right)\), so\[\begin{array}{rcccl}
x & = & \cos \left(\dfrac{5 \pi}{6}\right) & = & -\dfrac{\sqrt{3}}{2} \\
y & = & \sin \left(\dfrac{5 \pi}{6}\right) & = & \dfrac{1}{2} \\
\end{array} \nonumber \]Thus, the coordinates of \(P\) are \(\left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\), as shown below.
- On a unit circle, the coordinates of \(P\) are \(\left(\cos \left(\frac{\pi}{2}\right), \sin \left(\frac{\pi}{2}\right)\right)\), so\[x=\cos \left(\dfrac{\pi}{2}\right)=0 \quad \text { and } \quad y=\sin \left(\dfrac{\pi}{2}\right)=1 \nonumber \]The coordinates of \(P\) are \((0,1)\), as shown below.
Find the coordinates of the terminal point, \(P\), of an arc of length \(t\) starting at (1,0) on a unit circle.
- \(t=\pi\)
- \(t=\frac{\pi}{3}\)
- Answers
-
- \( (-1,0) \)
- \(\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\)
Using a Calculator to Compute the Values of Trigonometric Functions
Before moving forward, let's talk about using your calculator's Radian mode. In the previous section, we evaluated the trigonometric functions at the special radian angles (i.e., multiples of \( \pi/6 \), \( \pi/4 \), and \( \pi/3 \)). We now focus on evaluating the trigonometric functions at non-special radian angles (and, therefore, non-special real numbers).
If you use a scientific or graphing calculator, refer to your instruction manual on setting it to radian mode. The scientific calculator in Desmos is set to degree mode by default, so if you are using that technology, you need to click the "DEG" toggle so that "RAD" is showing; however, the graphing calculator in Desmos defaults to radian mode.
Setting the calculator to radian mode allows us to avoid converting from radians to degrees to evaluate trigonometric functions. First, change the calculator setting from Degree mode to Radian mode. Then enter\[\mathrm{SIN} \, \pi \, \div \, 3\nonumber \]and the calculator will return 0.8660254038. You can check that this number is a decimal approximation for \(\frac{\sqrt{3}}{2}\).
Use your calculator to find the sine and cosine of the following angles in radians. Round your answers to four decimal places.
- \(\theta=\dfrac{7 \pi}{4}\)
- \(\theta=3.5\)
- Solutions
-
- With your calculator in radian mode, enter\[\mathrm{COS} \, 7 \, \pi \, \div \, 4\nonumber \]and\[\mathrm{SIN} \, 7 \, \pi \, \div \, 4 \nonumber \]to find\[ \begin{array}{rcl}
\cos \left( \dfrac{7 \pi}{4}\right) & \approx & 0.7071067812 \\
\sin \left( \dfrac{7 \pi}{4} \right) & \approx & -0.7071067812 \\
\end{array} \nonumber \]Rounding to four decimal places gives \(\cos \left(\frac{7 \pi}{4}\right) \approx 0.7071\) and \(\sin \left(\frac{7 \pi}{4}\right) \approx -0.7071\). - Your calculator will give you the values\[ \begin{array}{rcl}
\cos (3.5) & \approx & -0.9364566873 \\
\sin (3.5) & \approx & -0.3507832277 \\
\end{array} \nonumber \]Rounding to four places, we have \(\cos (3.5) \approx -0.9365\) and \(\sin (3.5) \approx -0.3508\). Note that 3.5 radians is a third-quadrant angle, so the signs of the trigonometric values make sense.
- With your calculator in radian mode, enter\[\mathrm{COS} \, 7 \, \pi \, \div \, 4\nonumber \]and\[\mathrm{SIN} \, 7 \, \pi \, \div \, 4 \nonumber \]to find\[ \begin{array}{rcl}
Use your calculator to find the tangents of the following real numbers. Round your answers to four decimal places.
- \(t = \frac{5 \pi}{12}\)
- \(t = 5.2\)
- Answers
-
- 3.7321
- −1.8856
We can now use the trigonometric functions to model periodic behavior as functions of time instead of angles. Indeed, we now have the ability to use any variable as the argument of a trigonometric function.
The sunset time in Stockholm, Sweden, on the \(n^{ \text{th} }\) day of the year can be modeled by\[T=3.11 \sin \left(0.017 n-1.38\right)+6.03\nonumber \]where \(T\) is given in hours after noon. Find the sunset time on January 1 (day \(n=1\)) and on July 1 (day \(n=182\)).
- Solution
-
Evaluate the function for \(n=1\) to find\[T=3.11 \sin \left(0.017(1)-1.38\right)+6.03 \approx 2.99.\nonumber \]On January 1, sunset in Stockholm occurs about 2.99 hours after noon, or at 2:59 pm.
Evaluate the function at \(n=182\) to find\[T=3.11 \sin \left(0.017(182)-1.38\right)+6.03 \approx 9.11. \nonumber \]On July 1, sunset occurs about 9.11 hours after noon, or at 9:07 pm. (Actually, 10:07 pm, because of daylight saving time.)
Variable stars are important in astronomy because they are used to estimate distances. Their magnitude, or brightness, varies periodically and can be modeled by trigonometric functions. The star T Herculis reached its minimum magnitude on December 27, 2004, and \(t\) days later its magnitude is approximately\[M=10.2-2.2 \cos \left(0.038 t\right)\nonumber \]
- What was the magnitude of T Herculis on December 27, 2004?
- What was the magnitude of T Herculis on December 27, 2006 (730 days later)?
- Answers
-
- 8
- 12.09
Use the graph of the unit circle shown below to estimate \(\cos (2.5)\), \(\sin (2.5)\), and \(\tan (2.5)\).

- Solution
-
The circle is scaled in units of 0.1 radians, and an arc of 2.5 radians in standard position has its terminal point, \(P\), in the second quadrant. The coordinates of \(P\) are approximately \((-0.8,0.6)\), so we have\[\cos (2.5) \approx -0.8 \quad \text { and } \quad \sin (2.5) \approx 0.6. \nonumber \]To find \(\tan (2.5)\), we calculate \(\frac{y}{x}\).\[\tan (2.5)=\dfrac{y}{x} \approx \dfrac{0.6}{-0.8} = -0.75. \nonumber \]
Use the graph of the unit circle in the previous example to estimate \(\cos (4.2)\), \(\sin (4.2)\), and \(\tan (4.2)\).
- Answer
-
Approximately −0.49, −0.87, and 1.78, respectively.
Activity

- Use the unit circle to estimate the sine, cosine, and tangent of each arc of given length.
- 0.6
- 2.3
- 3.5
- 5.3
- Use the unit circle to estimate two solutions to each equation.
- \(\cos (t) = 0.3\)
- \(\sin (t) = 0.7\)
- Sketch the angle on the unit circle. Find the reference angle in radians, rounded to two decimal places, and sketch the reference triangle.
- 1.8
- 5.2
- 3.7
- Give a decimal approximation to two places for each angle, then the degree measure of each.
Radians 0 \(\dfrac{\pi}{12}\) \(\dfrac{\pi}{6}\) \(\dfrac{\pi}{4}\) \(\dfrac{\pi}{3}\) \(\dfrac{5\pi}{12}\) \(\dfrac{\pi}{2}\) \(\dfrac{7\pi}{12}\) \(\dfrac{2\pi}{3}\) \(\dfrac{3\pi}{4}\) \(\dfrac{5\pi}{6}\) \(\dfrac{11\pi}{12}\) \(\pi\) Decimal Approx. Degrees Radians \(\pi\) \(\dfrac{13\pi}{12}\) \(\dfrac{7\pi}{6}\) \(\dfrac{5\pi}{4}\) \(\dfrac{4\pi}{3}\) \(\dfrac{17\pi}{12}\) \(\dfrac{3\pi}{2}\) \(\dfrac{19\pi}{12}\) \(\dfrac{5\pi}{3}\) \(\dfrac{7\pi}{4}\) \(\dfrac{11\pi}{6}\) \(\dfrac{23\pi}{12}\) \(2\pi\) Decimal Approx. Degrees - On the unit circle above, plot the endpoint of each arc in standard position.
- \(\dfrac{\pi}{3}\)
- \(\dfrac{7\pi}{6}\)
- \(\dfrac{7\pi}{4}\)
Geometric Representations of the Circular Functions
We have already introduced the idea that, given an arc length \( t \) along the unit circle, \( \cos\left( t \right) \) is the \( x \)-value of the point where the arc length terminates and \( \sin \left( t \right) \) is the \( y \)-value; however, there are other interesting geometric interpretations of the circular functions of real number. To understand these interpretations better, the following activity should be explored independently or during class.
Part 1
Figure \( \PageIndex{ 3 } \) shows a unit circle centered at \(O\). The line through \(A C\) is tangent to the circle at \(A\). (Recall that a tangent to a circle is perpendicular to the radius that meets it.)

Figure \( \PageIndex{ 3 } \)
- What is the radius of the circle?
- Find line segments whose lengths are \(\cos \left(\theta\right)\) and \(\sin \left(\theta\right)\).
- Explain why \(\triangle O A C\) is similar to \(\triangle O B D\).
- Find a line segment in \(\triangle O A C\) whose length is \(\tan \left(\theta\right)\). Explain why your choice is correct.
- Find a line segment in \(\triangle O A C\) whose length is \(\sec \left(\theta\right)\). Explain why your choice is correct.
Part 2
Figure \( \PageIndex{ 4 } \) is another unit circle, with tangent \(B D\).

Figure \( \PageIndex{ 4 } \)
- What are the measures of the angles \(\angle O C D\) and \(\angle O C B\)?
- Explain why \(\triangle O C B\) is similar to \(\triangle O A C\).
- Find a line segment in \(\triangle O C B\) whose length is \(\tan \left(\theta\right)\). Explain why your choice is correct.
- Find a line segment in \(\triangle O C B\) whose length is \(\sec \left(\theta\right)\). Explain why your choice is correct.
- Explain why \(\triangle O C B\) is similar to \(\triangle D C O\).
- Find a line segment in \(\triangle D C O\) whose length is \(\csc \left(\theta\right)\). Explain why your choice is correct.
Domain and Range of the Circular Functions
By interpreting the trigonometric functions in terms of the unit circle definition (as circular functions), we can discuss their domains and ranges.
Interact: Move the point \(D\) to help you investigate the circular functions geometrically.
If \( t \) is the length of the arc along the unit circle, then we can see that, no matter how large or small, negative or positive, we make \( t \), the arc length will terminate at a point \( P\left( x,y \right) \) on the unit circle. Since \( x = \cos\left( t \right) \) and \( y=\sin\left( t \right) \), the cosine and sine functions are defined for all real numbers.
Moreover, whenever \( x=0 \), we know that \( \sec\left( t \right) = \frac{1}{x} \) and \( \tan\left( t \right) = \frac{y}{x}\) are both undefined. We know the values of \( x \) on the unit circle become \( 0 \) precisely when \( t = \pm \frac{\pi}{2} \) or \( \pm \frac{3 \pi}{2} \) or \( \pm \frac{5 \pi}{2} \). In general, these two functions are undefined at \( t = \frac{\pi}{2} + k \pi \), where \( k \) is an integer. A similar argument reveals the cosecant and tangent functions to be undefined when \( t k \pi\) (again, where \( k \) is an integer). The following theorem summarizes these results.
Let \( t \) be a real number and \( k \) be an integer. The domains of the circular functions are\[ \begin{array}{rcl}
\sin\left( t \right) \text{ and } \cos\left( t \right) & \quad & \text{All real numbers, or } \left( -\infty, \infty \right) \\
\tan\left( t \right) \text{ and } \sec\left( t \right) & \quad & \text{All real numbers except }t = \dfrac{\pi}{2} + k \pi \\
\cot\left( t \right) \text{ and } \csc\left( t \right) & \quad & \text{All real numbers except }t = k \pi \\
\end{array} \nonumber \]
While there is a way to write the domains of tangent, cotangent, secant, and cosecant in interval notation, it's a bit complex.
The activity, Geometric Interpretations of the Circular Functions, can be beneficial in visualizing the ranges of the circular functions. For example, Figure \( \PageIndex{ 3 } \) shows us that the values of the cosine and sine functions (which are the \( x \) and \( y \) coordinates of points along the unit circle) are always between \( -1 \) and \( 1 \), inclusive. Thus, the range of these functions is \( \left[ -1,1 \right] \).
Since the values of the tangent function can be interpreted as the slope of the ray emanating from the origin through the point \( P\left( x,y \right) \) on the unit circle, we can easily see that the tangent can get as large (both positively and negatively) as we want. This is because the slopes of these line can get as steep as we want (and they can even be zero). Hence, the range of the tangent function is \( \left( -\infty,\infty \right) \).
The following theorem states the ranges of all of the circular functions. While not incredibly useful now, they will become increasingly important as we move forward, and we should introduce them early so you can get used to them.
Let \( t \) be a real number. The ranges of the circular functions are\[ \begin{array}{rcl}
\sin\left( t \right) \text{ and } \cos\left( t \right) & \quad & \left[ -1,1 \right] \\
\tan\left( t \right) \text{ and } \cot\left( t \right) & \quad & \left( -\infty, \infty \right) \\
\sec\left( t \right) \text{ and } \csc\left( t \right) & \quad & \left( -\infty,-1 \right] \cup \left[ 1, \infty \right) \\
\end{array} \nonumber \]
Is it possible for \( \sec\left( t \right) = -\frac{1}{2} \)?
- Solution
- Since the range of the secant function is \( \left( -\infty,-1 \right] \cup \left[ 1, \infty \right) \), and \( -\frac{1}{2} \) is not in this interval, it is not possible for \( \sec\left( t \right) = -\frac{1}{2} \).
For each function, state a value the function could return and a value it could not.
- \( \cos\left( t \right) \)
- \( \csc\left( t \right) \)
- Answers
-
- 2 is not a possible output, but 1/2 is.
- 1/2 is not a possible output, but 2 is.
Footnotes
1 You should check that these coordinates satisfy the equation of the circle, \(x^2+y^2=4\).
2 Once again, you should check that these coordinates satisfy the equation of the circle, \(x^2+y^2=1\).
Skills Refresher
Review the following skills you will need for this section.
For Problems 1 - 6, simplify.
\(\dfrac{2}{3} + \dfrac{1}{6}\)
\(\dfrac{2x}{3} + \dfrac{x}{6}\)
\(\dfrac{3}{4} - \dfrac{5}{8}\)
\(\dfrac{3n}{4} - \dfrac{5n}{8}\)
\(2 - \dfrac{3}{4}\)
\(2b - \dfrac{3b}{4}\)
\(1 + \dfrac{3}{8}\)
\(m + \dfrac{3m}{8}\)
\(\dfrac{5}{6} - \dfrac{7}{6}\)
\(\dfrac{5q}{6} - \dfrac{7q}{6}\)
\(\dfrac{2}{3} - \dfrac{5}{3}\)
\(\dfrac{2p}{3} - \dfrac{5p}{3}\)
- Answers
-
a \(\dfrac{5}{6}\), b \(\dfrac{5x}{6}\)
a \(\dfrac{1}{8}\), b \(\dfrac{n}{8}\)
a \(\dfrac{5}{4}\), b \(\dfrac{5b}{4}\)
a \(\dfrac{11}{8}\), b \(\dfrac{11m}{8}\)
a \(\dfrac{-1}{6}\), b \(\dfrac{-q}{6}\)
a \(-1\), b \(-p\)
Homework
Vocabulary Check
-
A circle of radius 1 having center at the origin is called a(n) ___.
-
When considered as functions of arc length, we call the trigonometric functions ___ functions because they are defined by the coordinates of points on a unit circle.
Concept Check
-
Explain why \(\cos \theta \leq 1\) for any angle \(\theta\).
-
How many solutions are there to the equation \(\cos \left(\theta\right)=0.4\) between \(0^{\circ}\) and \(360^{\circ}\)?
-
On a unit circle, the ___ measure of the central angle and the ___ length it cuts off are the same value.
-
List the trigonometric functions having a domain of all real numbers.
-
List the trigonometric functions having a range of all real numbers.
-
Sketch a figure on a unit circle to illustrate each equation.
-
\(\sin \dfrac{3 \pi}{4}=0.7071\)
-
\(\cos 2.5=-0.8011\)
-
-
Write down the multiples of \(\frac{\pi}{12}\) from 0 to \(2 \pi\). Reduce each fraction.
-
Sketch arcs in standard position on a unit circle with the following lengths.\[s=\dfrac{\pi}{2}, \quad s=\dfrac{3 \pi}{4}, \quad s=\dfrac{\pi}{3}, \quad s=\dfrac{2 \pi}{3} \nonumber \]
True or False? For Problems 11 - 15, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.
-
Let \(P(x,y)\) be a point on the unit circle determined by an arc of length \(t\) from the point \((1,0)\) to \(P\). Then the coordinates of \(P\) are given by \[x=\sin \left(t\right), \quad y=\cos \left(t\right).\nonumber \]
-
If \(\beta \lt \alpha\), then \(\sin \left(\beta\right) \lt \sin \left(\alpha\right)\).
-
The circular functions are functions of real numbers. As such, we can set our calculator to either degree or radian mode to get approximations of these functions.
-
The domain of the tangent function includes all real numbers except for \( \frac{\pi}{2} \).
-
The range of the sine and cosine functions is -1 to 1, inclusive.
Basic Skills
For Problems 16 - 19, each point on the unit circle is the terminal point of a special angle in standard position. Give exact values for the radian measure, \(t\), of the angle, and the coordinates \((x, y)\) of the point.
-

\(a\) \(b\) \(c\) \(d\) \(t\) \(x\) \(y\) -

\(a\) \(b\) \(c\) \(d\) \(t\) \(x\) \(y\) -
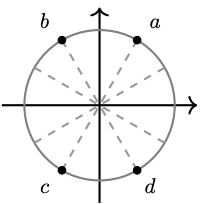
\(a\) \(b\) \(c\) \(d\) \(t\) \(x\) \(y\) -

\(a\) \(b\) \(c\) \(d\) \(t\) \(x\) \(y\) -
Complete the table.
\(\theta\) \( \sin\left( \theta \right) \) \( \cos\left( \theta \right) \) \( \tan\left( \theta \right) \) \(\dfrac{2\pi}{3}\) \(\dfrac{3\pi}{4}\) \(\dfrac{5\pi}{6}\) -
Complete the table.
\(\theta\) \( \sin\left( \theta \right) \) \( \cos\left( \theta \right) \) \( \tan\left( \theta \right) \) \(\dfrac{7\pi}{6}\) \(\dfrac{5\pi}{4}\) \(\dfrac{4\pi}{3}\) -
Complete the table.
\(\theta\) \( \sin\left( \theta \right) \) \( \cos\left( \theta \right) \) \( \tan\left( \theta \right) \) \(\dfrac{5\pi}{3}\) \(\dfrac{7\pi}{4}\) \(\dfrac{11\pi}{6}\)
For Problems 23 - 34, evaluate each function.
-
\( \sin\left( 45^{ \circ } \right) \)
-
\( \cos\left( 150^{ \circ } \right) \)
-
\( \cot\left( 270^{ \circ } \right) \)
-
\( \tan\left( 240^{ \circ } \right) \)
-
\( \sec\left( 315^{ \circ } \right) \)
-
\( \csc\left( 210^{ \circ } \right) \)
-
\( \cos\left( \frac{\pi}{6} \right) \)
-
\( \sin\left( \frac{3 \pi}{2} \right) \)
-
\( \tan\left( \frac{2 \pi}{3} \right) \)
-
\( \sec\left( \frac{7 \pi}{6} \right) \)
-
\( \csc\left( \frac{5\pi}{4} \right) \)
-
\( \cot\left( \frac{4\pi}{3} \right) \)
For Problems 35 - 40, use the unit circle to find all values of \( \theta \) between \( 0 \) and \( 2\pi \) for which the given equation is true.
-
\( \sin\left( \theta \right) = \frac{\sqrt{3}}{2} \)
-
\( \cos\left( \theta \right) = - \frac{\sqrt{3}}{2} \)
-
\( \tan\left( \theta \right) = -1 \)
-
\( \csc\left( \theta \right) = - 2 \)
-
\( \sec\left( \theta \right) = 1 \)
-
\( \cot\left( \theta \right) = \sqrt{3} \)
-
Estimate the \(x\)-coordinate of the points on the unit circle designated by each angle and complete the table. (Hint: Use symmetry in the second, third, and fourth quadrants.)
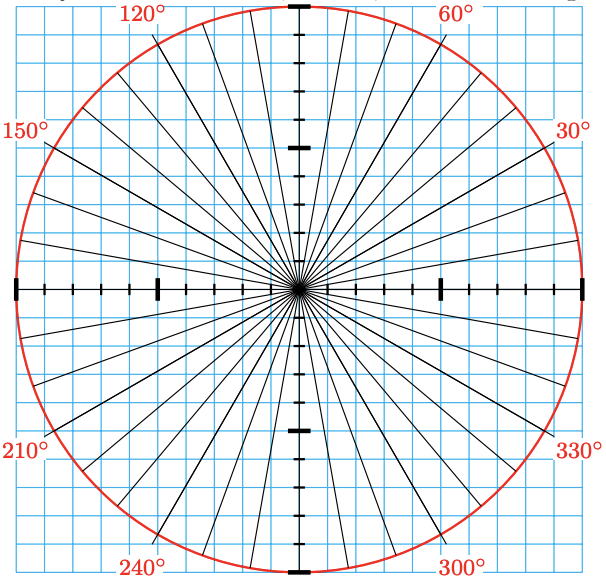
Angle \(0^{\circ}\) \(10^{\circ}\) \(20^{\circ}\) \(30^{\circ}\) \(40^{\circ}\) \(50^{\circ}\) \(60^{\circ}\) \(70^{\circ}\) \(80^{\circ}\) \(90^{\circ}\) \(x\)-coordinate Angle \(100^{\circ}\) \(110^{\circ}\) \(120^{\circ}\) \(130^{\circ}\) \(140^{\circ}\) \(150^{\circ}\) \(160^{\circ}\) \(170^{\circ}\) \(180^{\circ}\) \(x\)-coordinate Angle \(190^{\circ}\) \(200^{\circ}\) \(210^{\circ}\) \(220^{\circ}\) \(230^{\circ}\) \(240^{\circ}\) \(250^{\circ}\) \(260^{\circ}\) \(270^{\circ}\) \(x\)-coordinate Angle \(280^{\circ}\) \(290^{\circ}\) \(300^{\circ}\) \(310^{\circ}\) \(320^{\circ}\) \(330^{\circ}\) \(340^{\circ}\) \(350^{\circ}\) \(360^{\circ}\) \(x\)-coordinate -
Estimate the \(y\)-coordinate of the points on the unit circle designated by each angle and complete the table. (Hint: Use symmetry in the second, third, and fourth quadrants.)

Angle \(0^{\circ}\) \(10^{\circ}\) \(20^{\circ}\) \(30^{\circ}\) \(40^{\circ}\) \(50^{\circ}\) \(60^{\circ}\) \(70^{\circ}\) \(80^{\circ}\) \(90^{\circ}\) \(x\)-coordinate Angle \(100^{\circ}\) \(110^{\circ}\) \(120^{\circ}\) \(130^{\circ}\) \(140^{\circ}\) \(150^{\circ}\) \(160^{\circ}\) \(170^{\circ}\) \(180^{\circ}\) \(x\)-coordinate Angle \(190^{\circ}\) \(200^{\circ}\) \(210^{\circ}\) \(220^{\circ}\) \(230^{\circ}\) \(240^{\circ}\) \(250^{\circ}\) \(260^{\circ}\) \(270^{\circ}\) \(x\)-coordinate Angle \(280^{\circ}\) \(290^{\circ}\) \(300^{\circ}\) \(310^{\circ}\) \(320^{\circ}\) \(330^{\circ}\) \(340^{\circ}\) \(350^{\circ}\) \(360^{\circ}\) \(x\)-coordinate
For Problems 43 - 46, use the unit circle to estimate the sine, cosine, and tangent of each arc of given length.
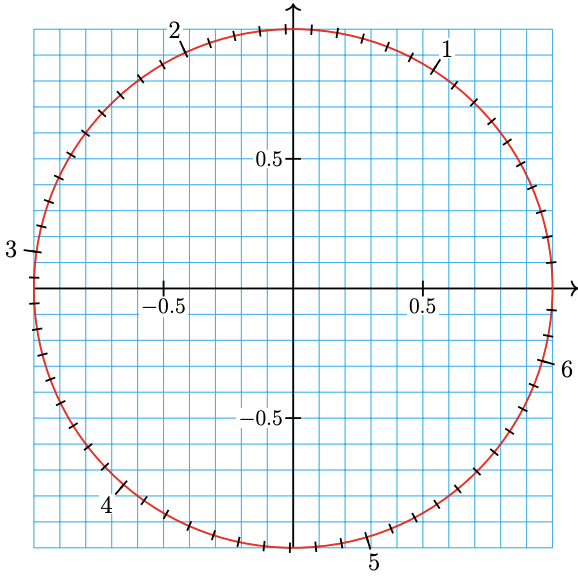
-
- 0.4
- 1.2
- 2
-
- 0.8
- 2.6
- 4
-
- 2.8
- 3.5
- 5
-
- 3
- 4.3
- 5.5
For Problems 47 - 52, use the unit circle to estimate two numbers with the given trigonometric value.

-
\(\cos t=0.3\)
-
\(\sin t=0.1\)
-
\(\sin t=-0.7\)
-
\(\cos t=-0.6\)
-
\(\tan t=\dfrac{-4}{9}\)
-
\(\tan t=\dfrac{8}{6}\)
Each of Problems 53 - 58 describes an arc in standard position on the unit circle. In which quadrant does the terminal point of the arc lie?
-
\(\sin s>0, \quad \cos s<0\)
-
\(\sin s<0, \quad \cos s>0\)
-
\(\cos t<0, \quad \tan t<0\)
-
\(\cos t>0, \quad \tan t<0\)
-
\(\sin x<0, \quad \tan x>0\)
-
\(\sin x>0, \quad \tan x<0\)
For Problems 59 - 64, without a calculator, decide whether the quantity is positive or negative.
-
\(\cos 2.7\)
-
\(\sin 4.1\)
-
\(\tan 3.8\)
-
\(\tan 5.4\)
-
\(\sin 2.2\)
-
\(\cos 4.9\)
Starting at \((1,0)\), you walk \(s\) units around a unit circle. For Problems 65 - 68, sketch a unit circle showing your position. What are your coordinates?
-
\(s=2.5\)
-
\(s=4.3\)
-
\(s=8.5\)
-
\(s=11\)
Synthesis Questions
For Problems 69 - 72, place the trigonometric values in order from smallest to largest. Use the figure to help you, but try not to use a calculator!

-
\(\sin 0.5, \quad \sin 1.5, \quad \sin 2.5, \quad \sin 3.5\)
-
\(\cos 1.6, \quad \cos 2.6, \quad \cos 3.6, \quad \cos 5.6\)
-
\(\cos 2, \quad \cos 3, \quad \cos 4, \quad \cos 5\)
-
\(\sin 2.8, \quad \sin 3.8, \quad \sin 4.8, \quad \sin 5.8\)
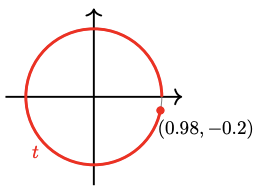
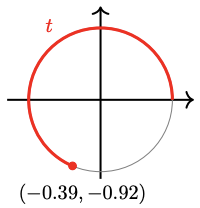
For Problems 73 - 76, the figure shows an arc of length \(t\), and the coordinates of its terminal point. Find the terminal point of each related arc given below, and give its sine, cosine, and tangent.
a \(2\pi - t\)
b \(\pi - t\)
c \(\pi + t\)
-

-
-
-
-
Use the figure to help you fill in the blanks.

-
As \(\theta\) increases from \(0^{\circ}\) to \(90^{\circ}, f(\theta)=\sin \theta\) _______ from _______ to _______.
-
As \(\theta\) increases from \(90^{\circ}\) to \(180^{\circ}, f(\theta)=\sin \theta\) _______ from _______ to _______.
-
As \(\theta\) increases from \(180^{\circ}\) to \(270^{\circ}, f(\theta)=\sin \theta\) _______ from _______ to _______.
-
As \(\theta\) increases from \(270^{\circ}\) to \(360^{\circ}, f(\theta)=\sin \theta\) _______ from _______ to _______.
-
-
Use the figure to help you fill in the blanks.
-
As \(\theta\) increases from \(0^{\circ}\) to \(90^{\circ}, f(\theta)=\cos \theta\) _______ from _______ to _______.
-
As \(\theta\) increases from \(90^{\circ}\) to \(180^{\circ}, f(\theta)=\cos \theta\) _______ from _______ to _______.
-
As \(\theta\) increases from \(180^{\circ}\) to \(270^{\circ}, f(\theta)=\cos \theta\) _______ from _______ to _______.
-
As \(\theta\) increases from \(270^{\circ}\) to \(360^{\circ}, f(\theta)=\cos \theta\) _______ from _______ to _______.
-
For Problems 79 and 80, use the grid provided below.

Use this grid for #75 and #76
-
Draw two different angles \(\alpha\) and \(\beta\) in standard position whose sine is 0.6.
-
Use a protractor to measure \(\alpha\) and \(\beta\).
-
Find the reference angles for both \(\alpha\) and \(\beta\). Draw in the reference triangles.
-
-
Draw two different angles \(\theta\) and \(\phi\) in standard position whose sine is \(−0.8\).
-
Use a protractor to measure \(\theta\) and \(\phi\).
-
Find the reference angles for both \(\theta\) and \(\phi\). Draw in the reference triangles.
-
For Problems 81 and 82, use the grid provided below.

Use this grid for #77 and #78
-
Draw two different angles \(\alpha\) and \(\beta\) in standard position whose cosine is 0.3.
-
Use a protractor to measure \(\alpha\) and \(\beta\).
-
Find the reference angles for both \(\alpha\) and \(\beta\). Draw in the reference triangles.
-
-
Draw two different angles \(\theta\) and \(\phi\) in standard position whose cosine is −0.4.
-
Use a protractor to measure \(\theta\) and \(\phi\).
-
Find the reference angles for both \(\theta\) and \(\phi\). Draw in the reference triangles.
-
For Problems 83 and 84, find all angles between \(0^{\circ}\) and \(360^{\circ}\) for which the statement is true.
-
-
\(\cos \theta = -1\)
-
\(\sin \theta = -1\)
-
\(\tan \theta = -1\)
-
-
-
Find two angles, \(0 \leq \theta \leq 360^{\circ}\), with \(\sin \theta = 0\).
-
Find two angles, \(0 \leq \theta \leq 360^{\circ}\), with \(\cos \theta = 0\).
-
For Problems 85 - 90, find two points on the unit circle with the given coordinate. Sketch the approximate location of the points on the circle. (Hint: what is the equation for the unit circle?)
-
\(x=0.2\)
-
\(x=-0.6\)
-
\(y=-0.35\)
-
\(y=0.7\)
-
\(x=\dfrac{-\sqrt{3}}{2}\)
-
\(y=\dfrac{1}{\sqrt{2}}\)
For Problems 91 - 96, find the angle in radians between 0 and \(2 \pi\) determined by the terminal point on the unit circle. Round your answer to hundredths.
-
(−0.1782, 0.9840)
-
(−0.8968, −0.4425)
-
(0.8855, −0.4646)
-
(0.9801, 0.1987)
-
(−0.7659, −0.6430)
-
(0.9602, −0.2794)
-
-
Sketch a unit circle and the line \(y=x\). Find the coordinates of the two points where the line and the circle intersect.
-
State your answers to part (a) using trigonometric functions.
-
-
-
Sketch a unit circle and the line \(y=-x\). Find the coordinates of the two points where the line and the circle intersect.
-
State your answers to part (a) using trigonometric functions.
-
-

-
Sketch a line that passes through the origin and the point (8,3). What is the slope of the line?
-
What is the angle of inclination of the line in radians, measured from the positive \(x\)-axis?
-
-

-
Sketch a line that passes through the origin and the point (3,8). What is the slope of the line?
-
What is the angle of inclination of the line in radians, measured from the positive \(x\)-axis?
-
For Problems 101 - 104, find an equation for the line with the given angle of inclination passing through the given point.
-
\(\alpha=\dfrac{\pi}{3},(4,2)\)
-
\(\alpha=\dfrac{5 \pi}{6},(-6,3)\)
-
\(\alpha=2.4,(5,-8)\)
-
\(\alpha=0.6,(-2,-3)\)
-
If \(\sec(\theta) = \dfrac{x}{4}\) for \(0 < \theta < \dfrac{\pi}{2}\), find an expression for \(\ln|\sec(\theta) + \tan(\theta)|\) in terms of \(x\).
Applications
-
The sunrise time in Wellington, New Zealand, on the nth day of the year can be modeled by\[S=1.93 \sin (0.016 n-1.13)+6.14 \nonumber \]where \(S\) is given in hours after midnight. Find the sunrise time on January 1 (day \(n=1\)), April 1 (day \(n=91\)), July 1 (day \(n=182\)), and on October 1 (day \(n=274\)).
-
The variable star RT Cygni reached its maximum magnitude on May 22, 2004, and \(t\) days later its magnitude is given by\[M=9.55-2.25 \cos (0.033 t) \nonumber \]Find the magnitude of RT Cygni on days \(t=0\), \(t=48\), \(t=95\), \(t=142\), and \(t=190\). (Note that smaller values of \(M\) denote brighter magnitudes.)
-
City Park features a circular jogging track with a radius of 1 mile centered on the open-air bandstand. You start jogging on the track 1 mile due east of the bandstand and proceed counterclockwise. What are your coordinates relative to the bandstand when you jogged five miles?
-
Silver Reservoir is a circular man-made lake with a radius of 1 kilometer. If you start at the easternmost point on the reservoir and walk counterclockwise for 4 kilometers, how far south of your initial position are you?
Use the results of Problem 110 for Problems 111 - 113.
-
Use similar triangles to show that the coordinates of a point \(P\) determined by angle \(\theta\) on a circle of radius \(r\) are \(x = r \cos \theta, y = r \sin \theta\). (See the figure below.)

-
The Astrodome in Houston has a diameter of 710 feet. If you start at the easternmost point and walk counterclockwise around its perimeter for 250 feet, how far north of your starting point are you?
-
The Barringer meteor crater near Winslow, Arizona, is 1182 meters in diameter. You start at the easternmost point on the crater's rim and walk counterclockwise around the edge. After walking for 1 kilometer, what is your position relative to your starting point?
-
One of the most intriguing features of Stonehenge is the position of the four Station Stones.
They form the corners of a rectangle inscribed in the Aubrey Circle on the perimeter of the henge, which has a diameter of 288 feet. A line from the center of the circle and perpendicular to the long edge of the rectangle points through the Slaughter Stones at the entrance of the henge and out to the Heel Stone. If you stood in the circle's center on the summer solstice, you would see the sun rise directly over the Heel Stone.

-
The sun rises \(48.6^{\circ}\) east of north on the summer solstice at Stonehenge. If the positive \(y\)-axis points north, find the coordinates of the henge entrance relative to its center.
-
The northernmost station stone is located \(66.6^{\circ}\) of arc counterclockwise from the entrance. Find its coordinates relative to the center of the henge.
-
Challenge Problems
-
Use similar triangles to show that the coordinates of point \(P\) on the unit circle shown below are \((\cos t, \sin t)\).
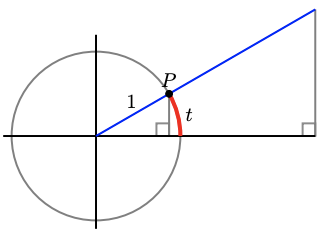
-
Use similar triangles to show that \(S T=\tan t\).



